Signale von Differenzialtransformatoren
Rauscharmer digitaler AM-Demodulator
Fortsetzung des Artikels von Teil 1
Signalaufbereitung mit Sigma-Delta-ADU
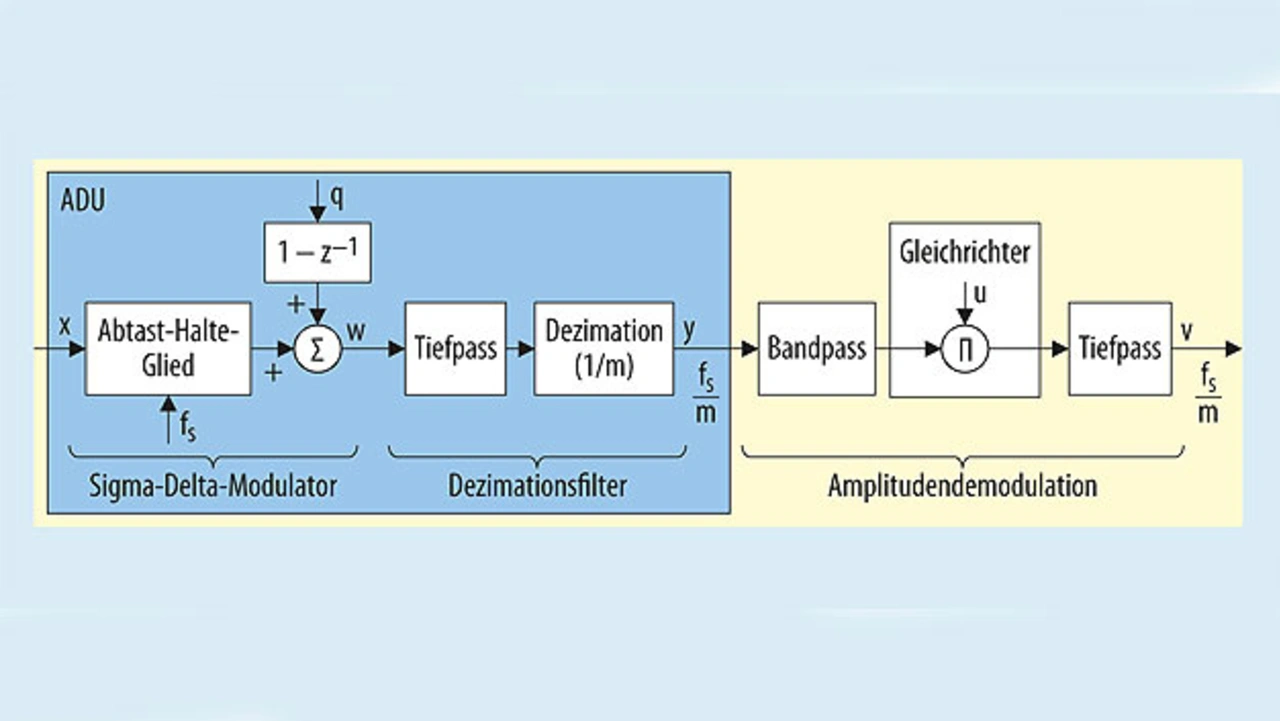
In Bild 3 ist ein Amplitudendemodulator zu sehen, der für den ADU in Bild 2 einen Sigma-Delta-Modulator erster Ordnung verwendet.
In dieser Anordnung erfolgt die Amplitudendemodulation durch den Gleichrichter, der durch die Multiplikation des Ausgangssignals des Bandpass (BP) mit dem Rechtecksignal (u) modelliert wird. Sie erfüllt die Funktion der Amplitudendemodulation, ist aber mit einer Einschränkung behaftet.
Da nämlich die Demodulation im dezimierten Frequenzbereich erfolgt, muss die primärseitige Erregerfrequenz auf Werte beschränkt bleiben, die unterhalb der Grenzfrequenz des Dezimationsfilters liegen.
Jobangebote+ passend zum Thema
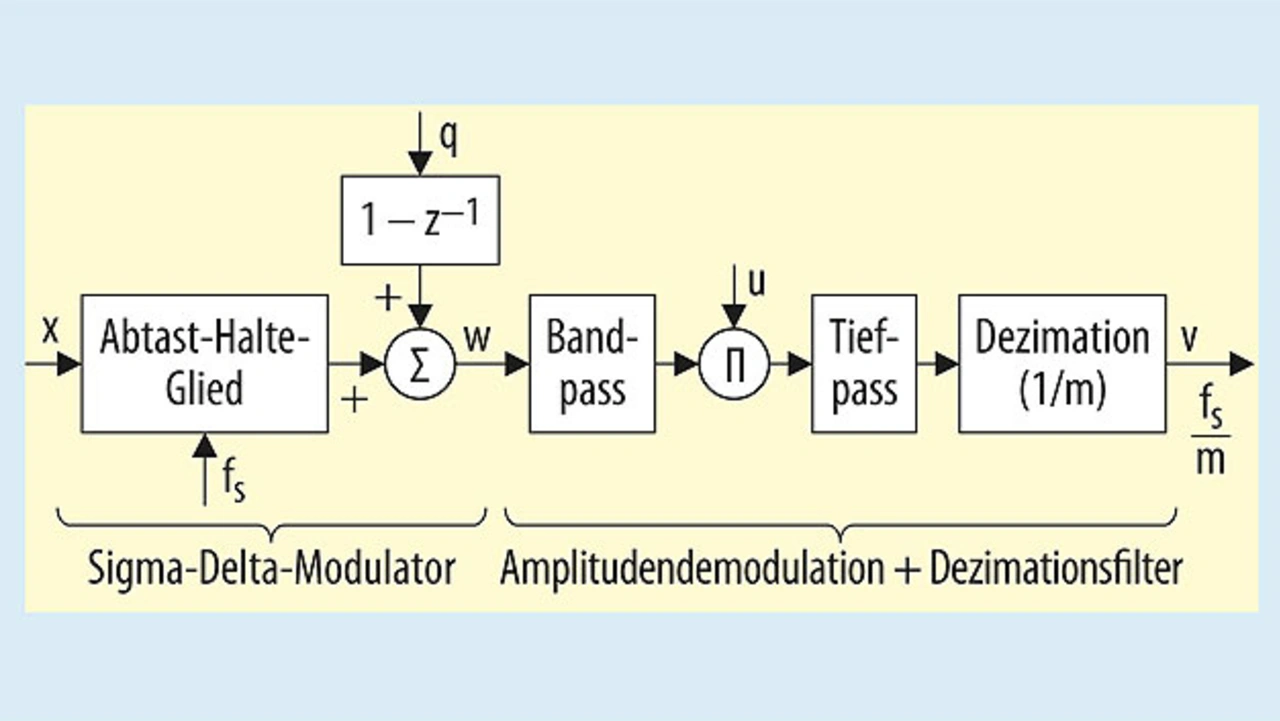
Um diese Beschränkung zu umgehen, wird die Reihenfolge der in Bild 3 dargestellten Blöcke geändert, wie in Bild 4 gezeigt. Der Bandpass in Bild 4 rückt an den Ausgang des Sigma-Delta-Modulators vor.
Die Blöcke können deshalb anders angeordnet werden, weil die in Bild 3 gezeigte Anordnung linear ist. Die neue Anordnung (Bild 4) lässt höhere primärseitige Erregerfrequenzen zu und kommt mit nur einem Tiefpassfilter aus, was eine platzsparendere Implementierung erlaubt. Eine Anordnung genau dieser Art wird
beispielsweise in Schaltkreisen für Differenzialtransformatoren wie dem PGA970 von Texas Instruments verwendet.
Signal-Rauschabstand eines Sigma-Delta-ADUs
Der SNR des in Bild 4 gezeigten Amplitudendemodulators hat unmittelbaren Einfluss auf die Genauigkeit der Positionsmessung. Es geht also darum, das Quantisierungsrauschen der in Bild 4 gezeigten Anordnung zu bestimmen und die mathematische Beschreibung des SNR herzuleiten.
Der Ausgang w des Sigma-Delta-Modulators lässt sich somit im zeitdiskreten Bereich durch Gleichung 4 beschreiben:
Darin ist z die z-Variable der Z-Transformation.
Aus Gleichung 4 lässt sich die Rauschübertragungsfunktion (NTF – Noise Transfer Function) als (1 – z–1) ableiten, und der quadrierte Betrag der NTF wird durch Gleichung 5 angegeben:
Mithilfe trigonometrischer Identitäten lässt sich Gleichung 5 zu Gleichung 6 umschreiben:
Unter der Annahme, dass es sich bei dem Bandpass um ein Rechteckfilter handelt, gibt Gleichung 7 die Varianz des Quantisierungsrauschens im interessierenden Bereich an:
Darin steht QLSB für das Quantisierungsrauschen.
Der Wert des Integrals der Rauschvarianz in Gleichung 7 wird durch Gleichung 8 angegeben:
Mit einigen algebraischen Umformungen lässt sich die Rauschvarianz der in Bild 4 gezeigten Anordnung zu dem in Gleichung 9 gezeigten Ausdruck vereinfachen:
Gestützt auf Gleichung 9 lassen sich die folgenden intuitiven Schlüsse ziehen:
- Je kleiner das Verhältnis fT/fS ist, umso geringer ist die Rauschvarianz. Das bedeutet, dass die Rauschvarianz umso niedriger ist, je kleiner die primärseitige Erregerfrequenz gegenüber der sekundärseitigen Abtastfrequenz ist. Aufgrund der Formung des Quantisierungsrauschens durch den Sigma-Delta-Modulator trifft dies tatsächlich zu.
- Die Rauschvarianz ist linear proportional zur Bandbreite B. Dies trifft intuitiv zu, weil die Rauschvarianz umso geringer ist, je kleiner der Bereich ist, über den das Quantisierungsrauschen integriert wird.
Auf der Basis von Gleichung 9 und dem Ausdruck für den Signal-Rauschabstand in Gleichung 3 lässt sich der Signal-Rauschabstand der in Bild 4 dargestellten Anordnung durch Gleichung 10 wiedergeben:
- Rauscharmer digitaler AM-Demodulator
- Signalaufbereitung mit Sigma-Delta-ADU
- Auswirkungen einer analogen Eingangsstufe
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Sigma-Delta-Modulator
PLDs als A/D-Wandler
Hohe Gleichtaktunterdrückung
Audio-Verstärker mit symmetrischem Eingang
Nanopower-Operationsverstärker – Teil 2
Einsatz als präzise Messverstärker: Messen der Stromstärke
Nanopower-Operationsverstärker – Teil 1
Einsatz als präzise Messverstärker: Gleichstromverstärkung
Differenzverstärker stabilisieren
Rauschverstärkung anpassen
Winzige Analogschaltungen
Operationsverstärker und Komparatoren im X2SON-Gehäuse
Encoder-IC
Genauer Messen dank schneller Interpolation
FMCW-Radarsysteme
Komplexe Signalverarbeitung im Basisband
Wie wir in Zukunft leben
Sensornetze für die Smart City
Elektronische Wasserzähler
SoC für den direkten Anschluss von Ultraschallsensoren
