Sigma-Delta-Modulator
PLDs als A/D-Wandler
Einfache A/D-Wandler lassen sich auf der Basis eines Sigma-Delta-Modulators und nachgeschaltetem digitalen Tiefpassfilter mit programmierbaren Logikbausteinen (PLD) realisieren. Doch wie genau sind sie? Wie hoch ist ihre Auflösung? Und wie groß ist der schaltungstechnische Aufwand?
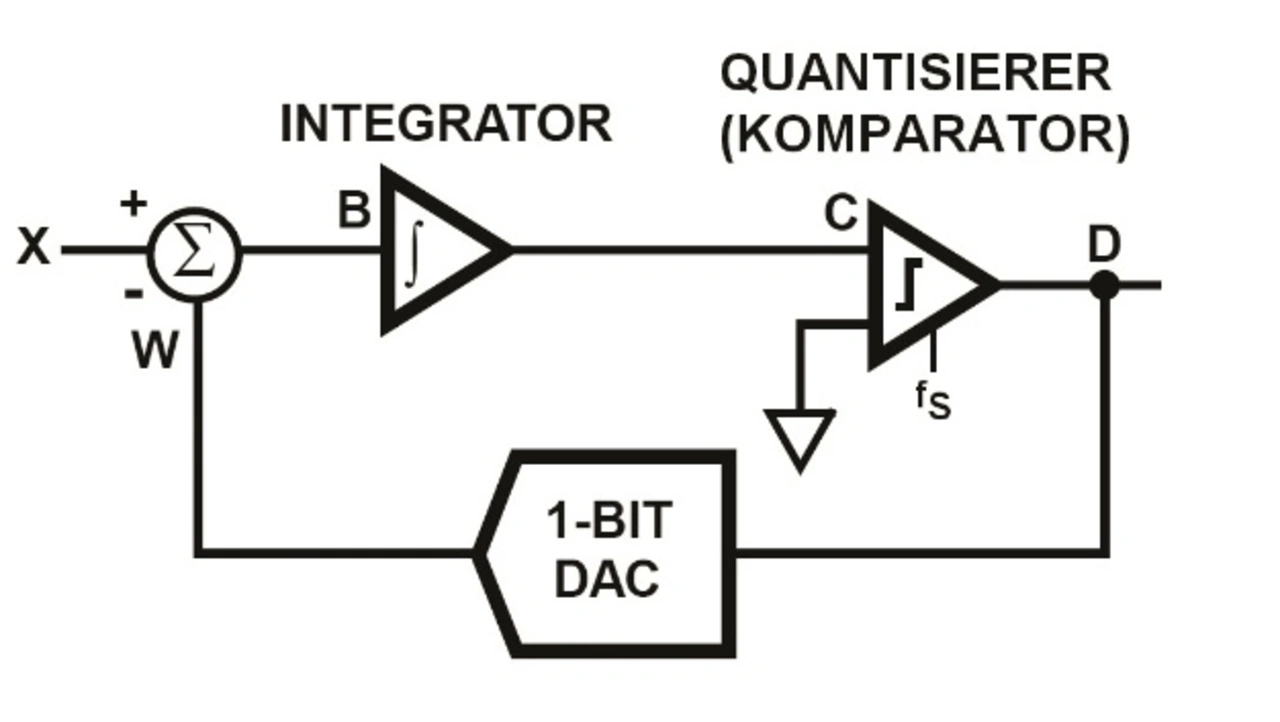
Sigma-Delta-Modulatoren (∑∆) erster Ordnung bestehen aus einem Subtrahierer, einem Integrierer, einem Quantisierer (Komparator) und einem 1 Bit breiten D/A-Wandler (Bild 1) [1]. Diese werden teilweise auch umgekehrt als Delta-Sigma-Modulatoren bezeichnet [2], da ja zunächst der Subtrahierer die Differenz (Δ) bildet und erst dann die Integration (∑) erfolgt. Der Quantisierer (Komparator) erhält als zusätzliches Eingangssignal die Abtastfrequenz fS. Dadurch kann sich das Ausgangssignal D nur zum Abtastzeitpunkt ändern und ist somit in fS quantisiert. Solche Modulatoren sind seit vielen Jahren bekannt [3].
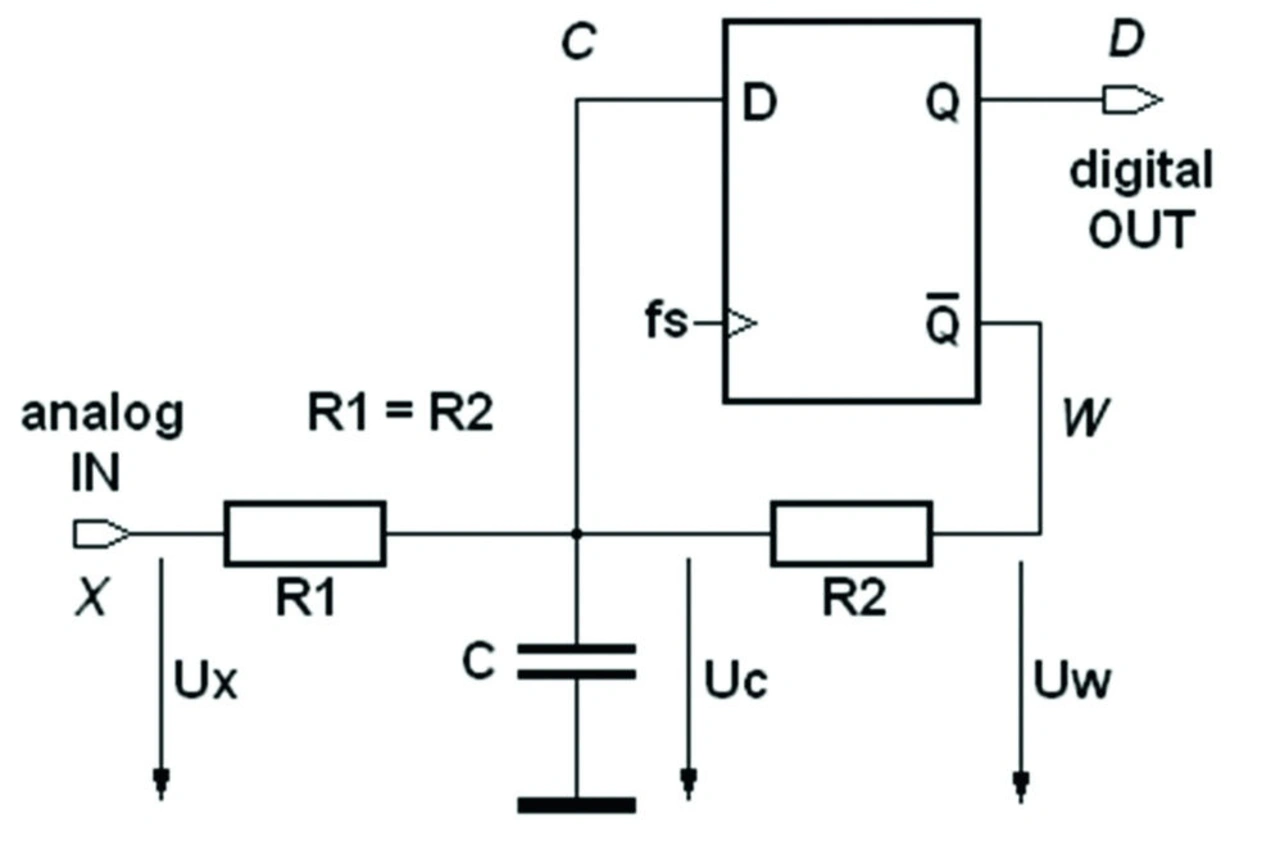
Ein solcher Modulator lässt sich im einfachsten Fall mit einem D-Flipflop, zwei Widerständen und einem Kondensator aufbauen (Bild 2). Die kursiv dargestellten Großbuchstaben sollen zeigen, welche Knoten aus Bild 1 in etwa den Knoten in Bild 2 entsprechen. Dadurch ist auch leicht zu erkennen, dass diese Vereinfachung im Wesentlichen durch eine höhere Ungenauigkeit erkauft wird. Die beim ∑∆-Modulator notwendige Subtraktion des D-A-gewandelten Ausgangssignals wird in der Schaltung aus Bild 2 dadurch bewerkstelligt, dass der Mittelwert des invertierten Ausgangssignals W zum Eingangssignal addiert wird. Dadurch müssen die Pegel an diesem Ausgang analogen Anforderungen genügen. Eine CMOS-Technologie ist deshalb zu bevorzugen, um für High und Low möglichst die UCC- und GND-Pegel zu erreichen
Jobangebote+ passend zum Thema
Eine weitere Ungenauigkeit wird dadurch eingebracht, dass der D-Eingang des Flipflops jetzt als analoger Komparator fungiert, was bedeutet, dass sein Trigger-Niveau die Übertragungsgenauigkeit des Systems bestimmt. Die Spannung am Kondensator UC bleibt immer in etwa auf diesem Trigger-Niveau. Denn sobald die Eingangsspannung UX ansteigt und somit auch UC, tendiert das D-Flipflop verstärkt High an /Q und somit Low an Q auszugeben, was die Spannung am Kondensator dann wiederum erniedrigt. Der ∑Δ-Modulator versucht also mit dem Mittelwert seiner Ausgangsimpulse der analogen Eingangsspannung zu folgen.
Eingangsspannungsbereich
Damit der Modulator aus Bild 2 nicht in die Begrenzung kommt, darf die Eingangsspannung UX nur in einem bestimmten Bereich liegen. Das D-Flipflop kann am digital-OUT-Ausgang D maximal kontinuierlich High-Impulse oder minimal kontinuierlich Low-Impulse ausgeben. Diesen beiden Zuständen ist dann auch die maximale und die minimale Eingangsspannung zugeordnet. Bei maximaler Eingangsspannung UX gibt das Flipflop am Q-Ausgang also nur noch High und am /Q-Ausgang nur noch Low aus. Der Pegel des /Q-Ausgangs wird somit zur Referenz für das Eingangssignal.
Vernachlässigt man den Eingangsstrom am Flipflop (CMOS) und nimmt man an, dass der Reststrom im Kondensator (Keramik) ebenfalls nicht zu berücksichtigen ist, ergibt sich, dass die Ströme in den beiden Widerständen R1 und R2 im Mittelwert gleich sein müssen. Dann lässt sich UX folgendermaßen berechnen:
Für die maximale Eingangsspannung gilt, dass der /Q-Ausgang konstant auf Low liegt. Somit ergibt sich:
Für die minimale Eingangsspannung gilt, dass der Q-Ausgang konstant auf High liegt. Somit ergibt sich:
Mit der Annahme, dass der Low-Pegel des Flipflops UW,low bei 0,00·UCC bis 0,05·UCC, der High-Pegel UW,high bei 0,95·UCC bis 1,00·UCC und der Triggerpegel UC laut [4] bei 0,45·UCC bis 0,55·UCC liegt, ergibt sich, dass UX,max bei 0,85·UCC bis 1,1·UCC liegt, UX,min bei –0,10·UCC bis +0,15·UCC. Der Eingangsspannungshub ΔUX berechnet sich dann zu:
Die Eingangsspannung kann also durchaus die Grenzen und den Hub der Versorgungsspannung UCC erreichen.
Um den dynamischen Eingangswiderstand zu bestimmen, ist zu berücksichtigen, dass die Spannung UC quasi konstant gehalten wird und dieser Knoten somit eine niedrige Impedanz besitzt. Deshalb ist der AC-Eingangswiderstand RIN,ac gleich R1. Bei der DC-Betrachtung ist zu berücksichtigen, dass der Widerstand R1 auf die Spannung UC führt. Dies bedingt, dass Strom in den Eingang hinein fließt (positiv), wenn die Eingangsspannung UX größer als UC ist, und umgekehrt
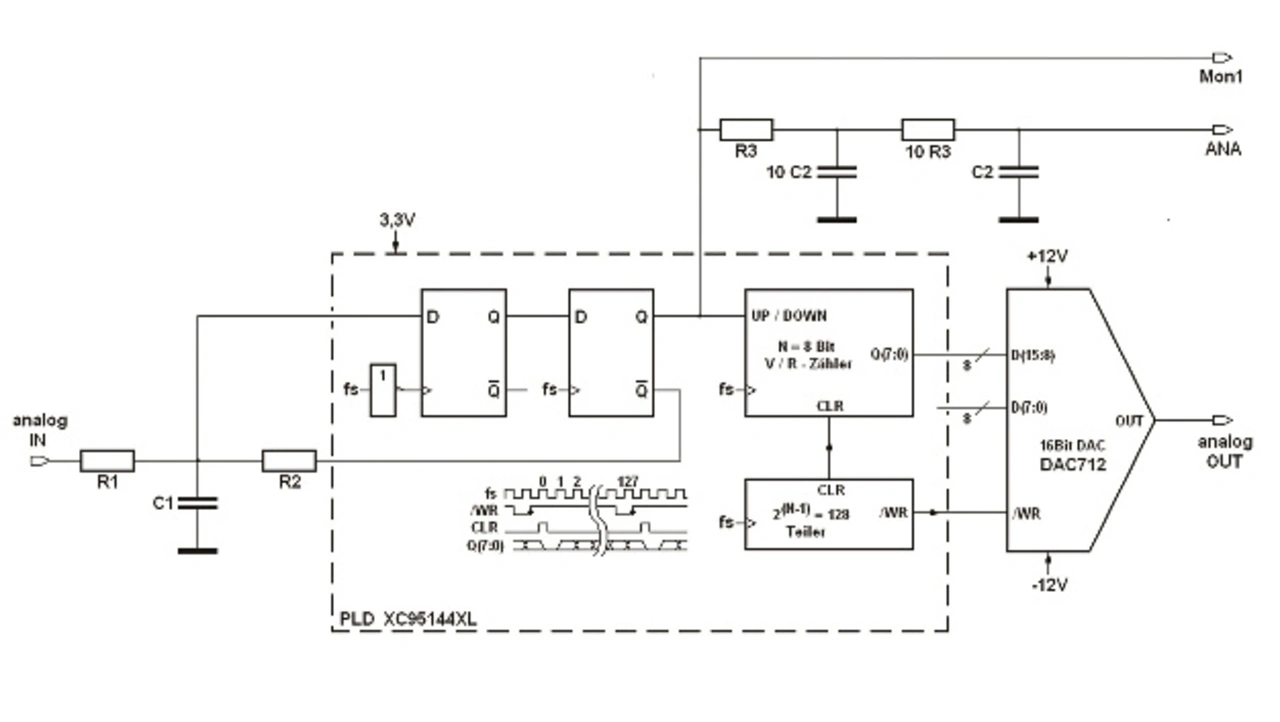
Ein Problem ergibt ich aus der Tatsache, dass der D-Eingang des Flipflops quasi immer auf Trigger-Niveau gehalten wird. Damit wird es eigentlich außerhalb der Spezifikation betrieben, denn eingangsseitige High- oder Low-Pegel sowie Setup- und Hold-Zeiten sind nicht eingehalten. Deshalb kann das Flipflop mit metastabilen Ausgangszuständen reagieren, was zum Beispiel dazu führt, dass der Q- und Q-Ausgang nicht mehr exakt gegenphasig sind. Um diese zu unterdrücken, ist es sinnvoll das Ausgangssignal mit einem zusätzlichen D-Flipflop abzutasten. Damit die Signalverzögerung im Regelkreis nicht zu groß wird, sollte man hier zur Abtastung die Gegenflanke der ersten Abtastung benutzen (Bild 3).
Um zusätzliche Ungenauigkeiten zu vermeiden, sind eventuell vorhandene Pull-up- oder Pull-down-Widerstände am Eingang des D-Flipflops im PLD zu deaktivieren. Eine vorhandene Keeper-Funktion, das heißt, ein Mitkopplungswiderstand im kΩ-Bereich über dem internen, nichtinvertierenden Eingangsverstärker, kann akzeptiert werden, da dieser im Verhältnis zur Eingangskapazität C die Signalspannung innerhalb eines Abtasttaktes sehr wenig verändert. Der ∑Δ-Modulator nach Bild 2 erreicht bei Vollaussteuerung einen Signal-Rausch-Abstand SNR von [5]:
Dabei ist fS die Abtast- und fO die obere Grenzfrequenz der Nutzsignalbandbreite.
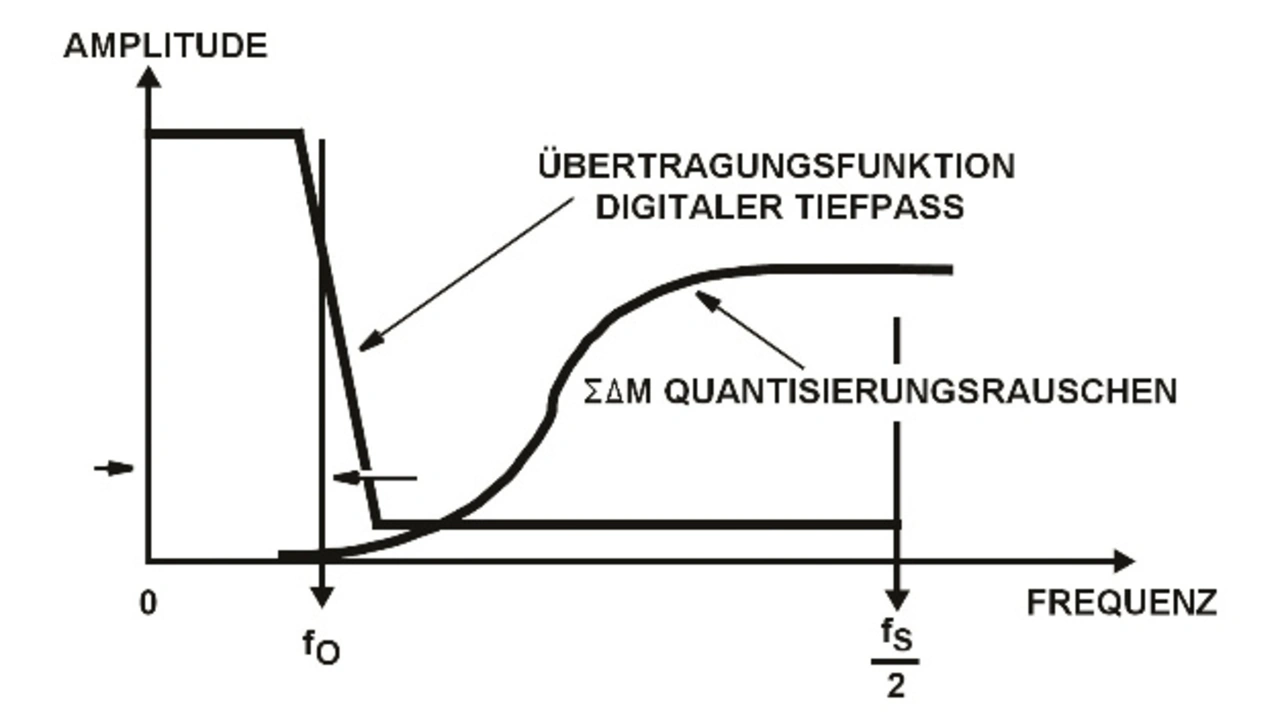
Leicht zu erkennen ist, dass eine doppelt so hohe Abtastfrequenz den Signal-Rausch-Abstand um den Faktor 23/2 (9 dB) erhöht, während bei Nyquist-A/D-Wandlern üblicherweise der Signal-Rausch-Abstand nur um den Faktor 21/2 (3 dB) steigt. Dies ist so, weil ein ∑Δ-Modulator das Rauschen zu höheren Frequenzen hin verschiebt, da die Widerstände und der Kondensator des Modulators wie ein Tiefpass für das Eingangssignal und ein Hochpass für das Rauschen wirken. Ein normaler A/D-Wandler hingegen verteilt das Rauschen gleichmäßig über der Frequenz. Bild 4 zeigt, dass das Rauschen ab fO ansteigt und bei fS/2 konstant bleibt.
Der Wert für fO ergibt sich aus der Kombination von R1, R2 und C aus Bild 2, wobei R1 und R2 quasi parallel liegen:
Sind R1 und R2 gleich groß, ergibt sich für fO folgender Zusammenhang:
Aus der Formel für das SNR ergibt sich, dass bei einer Abtastfrequenz von 12 MHz und einer Nutzsignalbandbreite fO von 14,4 kHz ein Signal-Rausch-Abstand von 5743 oder 75,2 dB erzielt werden kann. Es ist also durchaus sinnvoll, das Ausgangssignal des ∑Δ-Modulators im nachfolgenden digitalen Tiefpassfilter mit acht oder mehr Bits aufzulösen.
- PLDs als A/D-Wandler
- Digitaler Tiefpassfilter
- Frequenzgang
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Analoge Signalverarbeitung im μC
MSP430 mit programmierbaren Analogschaltungen
Signale von Differenzialtransformatoren
Rauscharmer digitaler AM-Demodulator
Interview mit Analog-Guru Bob Dobkin
»Wir haben von Digital sehr profitiert«
