Analyseverfahren spart Rechenzeit
Polynome schneller auf Primitivität prüfen
Fortsetzung des Artikels von Teil 2
Primitive Polynome und ihre Bestimmung
Polynome, die nicht teilbar sind, werden als irreduzible bezeichnet. Diese werden in zwei Gruppen aufgeteilt, primitive Polynome mit einer maximalen Zykluslänge ZLmax = 2r – 1 und nichtprimitive Polynome, die eine kleinere Zykluslänge als ZLmax aufweisen. Die Zykluslänge von nichtprimitiven Polynomen ist stets ein Teiler von 2r – 1 oder ein Produkt der Primfaktoren von 2r – 1 [2]. Die irreduziblen Polynome werden häufig in der Sicherheitstechnik eingesetzt, da zum einen die nichtprimitiven Polynome in der Regel eine höhere Hammingdistanz HD = d aufweisen und die primitiven Polynome dagegen die größte mögliche Zykluslänge liefern. Ein Polynom mit einer HD von d erkennt sämtliche m-Bitfehler bis m < d, und trägt somit zum geringen Zuwachs der Restfehlerwahrscheinlichkeit RW im Vergleich zum Polynom mit einem geringen d bei. Mit Überschreiten der Zykluslänge ZL fällt die Hammingdistanz d auf zwei, und die RW nimmt in der Regel stark zu, da im weiteren Verlauf nur noch 1-Bitfehler erkannt werden können.
Primitive Polynome haben somit bis n = ZLmax eine HD von drei, d.h., sie sind in der Lage sämtliche Bitfehler bis zum 2-Bitfehler erkennen zu können und leisten dementsprechend einen angemessenen Beitrag zur Begrenzung der RW. Nach Überschreiten der Zykluslänge ZL verliert das Polynom im weiteren Verlauf seine Wirksamkeit. Das Polynom gilt als erschöpft.
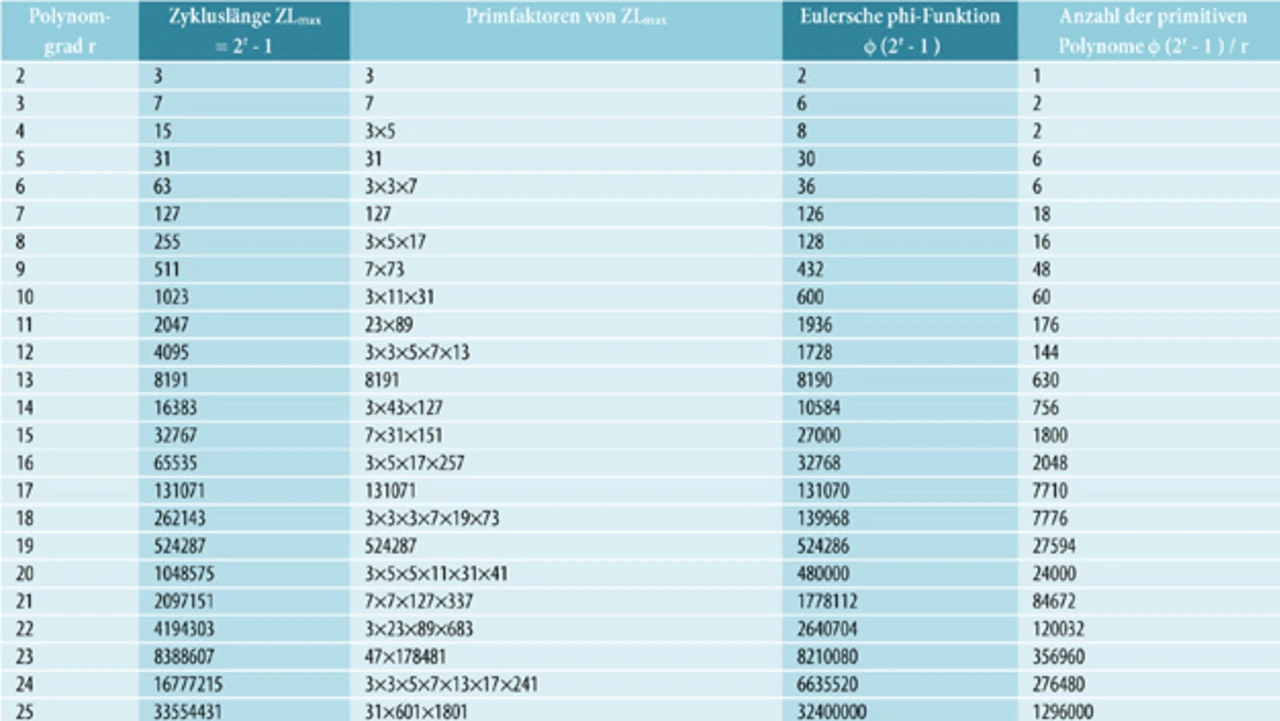
Die Anzahl der primitiven Polynome r-ten Grades kann mithilfe der Eulerschen phi-Funktion für n = 2r - 1 berechnet werden. Die phi-Funktion ist eine nummerische Funktion, und ϕ(n) gibt für eine positive Ganzzahl n an, wie viele teilerfremde Zahlen kleiner als n es zu ihr gibt. Die phi-Funktion hat große Bedeutung in der Kryptographie. Hier lässt sich mit der Hilfe der phi-Funktion die Anzahl der primitiven Polynome r-ten Grades schnell berechnen. Sie beträgt ϕ(2r - 1) / r. Bemerkenswert ist, dass die Anzahl der irreduziblen Polynome r-ten Grades stets ≥ ϕ(2r - 1) / r beträgt, da die nichtprimitiven Polynome noch dazu addiert werden. Die Gleichheit kommt nur dann vor, wenn 2r - 1 selbst eine Primzahl ist. Die sämtlichen irreduziblen Polynome r-ten Grades sind dann primitiv. In diesem Fall existieren keine nichtprimitiven Polynome.
Läuft ein LFSR frei, so wiederholt sich sein anfänglicher Zustand nach ZL Takten. Diese klassische Betrachtungsweise ist ineffektiv und kann die Bestimmung von ZL für ein primitiven Polynom 32-ten Grades 30 Minuten oder längere Rechenzeit benötigen. Wird stattdessen mit den Potenzen der Transformationsmatrix Tm gearbeitet, so gewinnt man mit 33 Matrizen-Multiplikationen die Matrix TmZLmax für ein 32-bit-Polynom. Ist die Matrix TmZLmax eine Einheitsmatrix E(32), so kann sie jeden beliebigen Zustand auf sich selbst abbilden. Ist die Matrix TmZLmax ≠ E(r), so ist das Polynom reduzibel. Eine positive Bestätigung dieser Matrix als eine Einheitsmatrix E(r) ist jedoch kein Beweis, dass das untersuchte Polynom ein irreduzibles Polynom ist. Der Nachweis der Irreduzibilität eines Polynoms ist aufwendig, die Primitivität lässt sich dagegen etwas leichter nachweisen.
Die Bedingung, die Matrix TmZLmax = E(r), ist eine notwendige aber keine hinreichende Bedingung für ein primitives Polynom. Für die nichtprimitiven Polynome gilt jedoch auch, dass die Matrix TmZLmax = E(r) ist. Deshalb muss zusätzlich sichergestellt werden, dass kein nichtprimitives Polynom vorliegt. Die Zykluslänge ZL eines nichtprimitiven Polynoms ist stets ein Teiler von ZLmax = 2r – 1 oder ein Produkt von Primfaktoren von 2r – 1. Zum Nachweis der Primitivität müssen demach folgende zwei Bedingungen erfüllt werden:
- Die Matrix TmZLmax ist eine Einheitsmatrix.
- Die Matrix TmZL ist keine Einheitsmatrix,
für:
ZL = ein Teiler von 2r – 1 oder
ZL = ein beliebiges Produkt von Primfaktoren von 2r – 1.
Jobangebote+ passend zum Thema
Der hier vorgestellte Algorithmus ist sehr effektiv und bestimmt abhängig von r im Bruchteil einer Sekunde, ob ein Polynom primitiv ist. Die benötigte Rechenzeit für ein 61-bit-Polynom beträgt 5 s zur Bestimmung von den ersten zwei primitiven Polynomen. Die einzige Schwierigkeit stellt die Bestimmung der Primfaktoren von 2r – 1 dar. Das Softwareprogramm Matlab zum Beispiel kann bis r = 53 die Primfaktoren schnell berechnen. Mit dem Einsatz der Symbolic Toolbox von Matlab ist eine Primfaktorbildung bis r = 1023 möglich, dies benötigt jedoch eine hohe Rechenzeit und wird nicht empfohlen. Für r = 512 braucht das Programm zur Bildung der Primfaktoren 17 Minuten, was noch akzeptabel ist. In Tabelle 2 sind Primfaktoren von 2r – 1, sowie die Eulersche phi-Funktion, ϕ(2r – 1) für r-Werte bis 68 zusammengestellt. Sie kann bei der Prüfung der Primitivität eines Polynoms hilfreich sein.
Mit dem hier vorgestellten Verfahren ist es möglich, eine Gesamtheit von 2048 primitiven Polynomen 16-ten Grades in 40 s zu bestimmen. Für r = 32 gibt es mehr als 67 Millionen primitive Polynome. Sie alle zu bestimmen ist wenig sinnvoll. Interessant ist jedoch die nächsten 10 bis 15 Polynome ab einem vorgegebenen Startwert (binärer Wert des Polynoms) zu bestimmen. Der Einsatz von Matlab erlaubt die Analyse von Polynomen bis zu einem maximalen Grad von 53, da die Berechnungen auf maximal 16 Stellen (253 ≈ 9E15 ) begrenzt sind. So ist es möglich die fünf niederwertigsten Polynome 53-ten Grades in weniger als 10 s zu ermitteln. Die Analyse vereinfacht sich erheblich, wenn die maximale Zykluslänge ZLmax = 2r – 1 eine Primzahl, eine sogenannte Mersenne-Primzahl ist, wie es für das oben genannte Beispiel mit r = 61 der Fall ist. Es ist dann möglich Polynome mit r > 53 zu analysieren, da die Primfaktorbildung entfällt. Wenn die maximale Zykluslänge ZLmax eines primitiven Polynoms eine Mersenne-Primzahl darstellt, so gibt es keine Obergrenze von r zur Bestimmung von primitiven Polynomen. Dies ist dann eine Frage der verfügbaren Rechenleistung, wie es Tabelle 3 verdeutlicht.
| Laufende Nummer der Mersenne- Primzahl (MP) | Polynom- | MP = 2r - 1 | Anzahl der Stellen | Erste zwei primitive Polynome mit dem kleinsten Polynomwert in binärer Darstellung | Benötigte CPU-Zeit zur Bestimmung des Polynoms [s] |
|---|---|---|---|---|---|
| 9 | 61 | 2305843009213693951 | 19 | 1… (55 Nullen) …100111 | 4,9 |
| 1… (55 Nullen) …111111 | 0,1 | ||||
| 12 | 127 | 17014118346046923173 1687303715884105727 | 27 | 1… (125 Nullen) …11 | 3 |
| 1… (119 Nullen) …10000001 | 4 | ||||
| 13 | 521 | 68647976601306097149 | 157 | 1… (511 Nullen) …1001101011 | 1558 |
| 1… (510 Nullen) …1010000101 | 950 |
Tabelle 3. Diese primitiven Polynome haben eine Zykluslänge, die einer Mersenne–Primzahl (Mp) entspricht.
Literatur
[1] Merchant, K.: Cyclic Redundancy Chek für die industrielle Kommunikation – Probleme, Nutzen und Risiken. De Gruyter Oldenbourg Verlag, 2013, ISBN: 978-3-486-74193-3.
[2] Merchant, K.: BCH-Code zum Anfassen, Elektronik 2007, H. 21, S. 66–70, www.elektroniknet.de/kommunikation/sonstiges/artikel/565.
Dipl.-Phys. Kamal Merchant |
|---|
ist in Bombay geboren. Nach dem Studium der Physik an den Universitäten Bombay und Freiburg war er von 1968 bis 1976 bei der Firma AEG Telefunken in Heilbronn im Bereich Forschung tätig. Bis 1979 war er dann bei der Fa. Litef in Freiburg im Bereich Systementwicklung beschäftigt. Von 1979 bis zu seiner Pensionierung im Mai 2003 war er bei der Fa. Siemens in Erlangen tätig. Der Schwerpunkt seiner Arbeiten liegt in der Beurteilung und Bewertung von neuen Techniken hinsichtlich der Risiken und Chancen beim Einsatz. Von 2003 bis Anfang 2012 war er als wissenschaftlicher Berater beim Institut für Arbeitssicherheit (IFA) in Sankt Augustin tätig. |
philosoph100@gmx.de
- Polynome schneller auf Primitivität prüfen
- Eigenschaften von LFSR
- Primitive Polynome und ihre Bestimmung