Oberflächenmontierte Bauteile
Wärmewiderstände im Griff haben
Da die Komponenten- und die Leistungsdichte auf modernen Platinen weiter zunehmen, wird das Wärmemanagement immer wichtiger. Nur so ist sichergestellt, dass beispielsweise SMD-Widerstände ihre vorgeschriebenen Betriebstemperaturgrenzen nicht überschreiten.
Elektrische Widerstände führen ihre Verluste (I2·R) als Wärme ab, wodurch deren Temperatur steigt. Sobald ein Temperaturgefälle entsteht, beginnt Wärme zu fließen. Nach einer gewissen Zeit – abhängig von der Wärmekapazität und den Wärmeleiteigenschaften der Komponente – wird ein stationärer Zustand erreicht. Der konstante Wärmestrom PH entspricht der abgeleiteten elektrischen Leistung Pel (Bild 1).
Jobangebote+ passend zum Thema
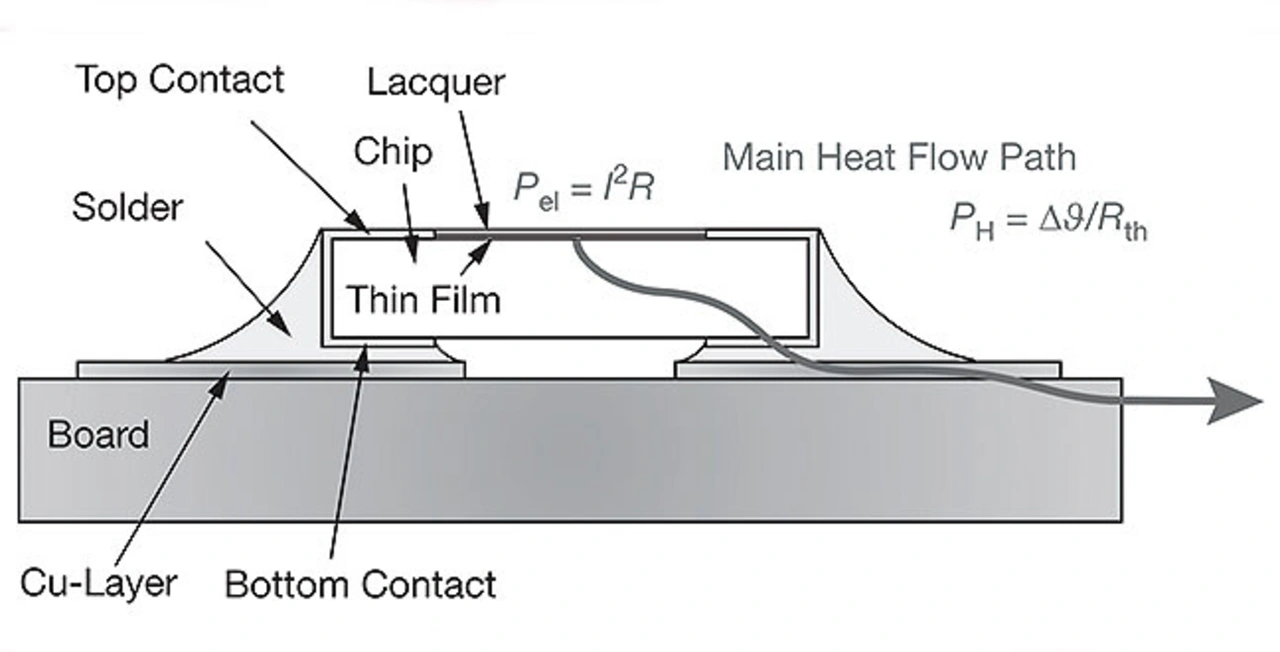
Da die Art der Wärmeleitung durch einen Körper dem ohmschen Gesetz ähnelt, ergibt sich für den Wärmestrom folgender Zusammenhang, siehe auch Kasten »Grundlagen Wärmeübertragung«:
Dabei gilt:
Rth ist der Wärmewiderstand und wird in K/W angegeben. Dieser ist für die meisten Materialien und Temperaturbereiche, die für elektronische Anwendungen von Interesse sind, unabhängig von der Temperatur.
| Grundlagen der Wärmeübertragung |
|---|
|
Wärmeenergie kann durch drei grundlegende Mechanismen übertragen werden: Wärmeleitung (Conduction), Wärmekonvektion und Wärmestrahlung (Radiation). ➔ Wärmeleitung Der Wärmestrom für die Wärmeleitung ist proportional zum eindimensionalen Gradienten dϑ/dx, wobei λ in der Dimension W/(m·K) die spezifische Wärmeleitfähigkeit und A die Querschnittsfläche für den Wärmestrom ist: Für einen einfachen kubischen Körper mit der Länge L und zwei parallelen Grenzflächen A bei unterschiedlichen Temperaturen ϑ1 und ϑ2 lautet die Gleichung für den Wärmeübergang: ➔ Konvektion Der Wärmestrom für Konvektion kann ähnlich wie für die Wärmeleitung beschrieben werden: Dabei sind α der Konvektionskoeffizient, A die Oberfläche bei der Temperatur ϑ1 des Objekts und ϑ2 die Temperatur des umgebenden Mediums (z. B. Luft). Der Koeffizient α umfasst die Materialeigenschaften des Mediums (Wärmekapazität und Viskosität) und die Bedingungen der Bewegung (Durchflussmenge, erzwungene/freie Konvektion und geometrische Formen). Außerdem hängt sie auch von der Temperaturdifferenz ϑ1−ϑ2 selbst ab. Diese Gleichung sieht also einfach aus, aber zur Lösung von Wärmeübertragungsproblemen ist der Koeffizient α fast immer anzunähern oder experimentell zu bestimmen. ➔ Wärmestrahlung Der Wärmestrahlungsfluss kann durch das Stefan-Boltzmann-Gesetz beschrieben werden, was zu einem Nettostrom zwischen zwei Objekten mit unterschiedlichen Temperaturen ϑ1 und ϑ2 führt, wobei ein identischer Emissionsgrad und eine identische Oberfläche angenommen werden. Dabei ist ε der Emissionsgrad, σ die Stefan-Boltzmann-Konstante und ϑ ist die Temperatur einer Oberfläche A. Die Wärmeübertragung durch Strahlung wird im Rahmen dieses Artikels jedoch nicht berücksichtigt, da der Beitrag bei niedrigen Temperaturen gering ist. Normalerweise werden mehr als 90 Prozent der Gesamtwärme durch Wärmeleitung abgeführt. Für die Infrarot-Wärmebildtechnik ist die Gleichung für die Wärmestrahlung jedoch von grundlegendem Interesse. |
- Wärmewiderstände im Griff haben
- Wärmewiderstand modellieren
- Wärmewiderständen experimentell bestimmen
- Zusammenfassung