HF-Messtechnik
Richtig messen im Zeit- und Frequenzbereich
Fortsetzung des Artikels von Teil 1
Die Bitfehlerrate steigt bei Signalverzerrungen
Die obigen Beispiele waren recht einfach. Die Wirklichkeit ist etwas komplizierter. Man muss nämlich etliche Dinge zusätzlich beachten:
- Laufen alle Frequenzen gleich schnell durch das Filter? Wenn nicht, wie verändert das die Kurvenform?
- Unterliegen alle Signalfrequenzen im Durchlassband der gleichen Dämpfung? Einige Filterdesigns weisen im Durchlassband eine Welligkeit auf (eine sich ändernde Dämpfung), andere zeigen eine Überhöhung kurz vor der Grenzfrequenz. Wie verändert das die Kurvenform?
- Verändert man das Signalspektrum durch Dämpfung, Verstärkung oder Änderung der Phasenbeziehung zwischen den Spektralelementen des Signals, ändert sich die Kurvenform. Ist diese Verzerrung d tolerabel?
Bei der Konstruktion eines Filters muss man wissen, ob der Zeitbereich oder der Frequenzbereich Priorität hat. Einige Filterformen bieten beispielsweise eine exzellente Dämpfung im Sperrbereich auf Kosten einer Verzerrung der Kurvenform.
Ein digitales Kommunikationssystem kann nur ordentlich arbeiten, wenn der Empfänger Einsen korrekt als Einsen interpretiert und Nullen als Nullen. Einen Fehler bei dieser Interpretation nennt man einen Bitfehler. Die Systemleistung bewertet man allgemein nach der Bitfehlerrate (BER), also dem Verhältnis von fehlerhaft empfangenen zu allen empfangenen Bits. Ein typischer Wert ist ein Fehler pro Billion empfangener Bits. Man erreicht eine niedrige BER durch einen deutlichen Unterschied zwischen den Logikpegeln für 0 und 1 und weiterhin dadurch, dass die Entscheidung, ob ein Bit 0 oder 1 ist, zeitlich möglichst weit entfernt von Pegelwechseln stattfindet. Der „Entscheidungszeitpunkt“ liegt üblicherweise in der Mitte der Bitzeit und in der Mitte zwischen den beiden Logikpegeln. Weicht das Signal vom Ideal ab und kommt den Grenzen nahe, steigt die Wahrscheinlichkeit einer Fehlentscheidung. Wenn das Signal also nicht die ideale, rechteckige Form aufweist, ist die BER in Gefahr. In sehr schnellen digitalen Kommunikationsnetzen liegt die Verzerrung der Signalform oft daran, dass sich das Signalspektrum beim Durchlauf des Signals durch das System ändert. Die oben besprochenen Überlegungen zu Filtern gelten sinngemäß genauso in schnellen Digitalsystemen.
Will man die Ursache einer Verzerrung der Kurvenform finden, fällt der erste Verdacht immer auf den Übertragungskanal, also das Medium, das das Signal vom Sender zum Empfänger trägt (etwa eine Leiterbahn in einem PC, ein Kabel oder ein Stück Glasfaser). Die meisten Übertragungskanäle wirken wie Tiefpässe. Es gibt verschiedene Gründe für die Dämpfung hoher Frequenzen beim Durchlauf eines Signals durch einen Übertragungskanal. Auf Leiterplatten oder in Kabeln weist das Isola-tionsmaterial möglicherweise bei höheren Frequenzen höhere Verluste auf als bei niedrigen. Höhere Frequenzen nutzen tendenziell nur die äußere Schicht eines Leiters und nicht den gesamten Querschnitt. Das erhöht den effektiven Widerstand und somit die Dämpfung. Selektive Dämpfung des höherfrequenten Teils des Spektrums eines Digitalsignals wirkt so wie oben anhand eines Rechtecksignals demonstriert, das durch einen Tiefpass läuft: Die Flanken werden flacher. Bei einer Glasfaser entsteht Hochfrequenzverlust dadurch, dass das Licht, das ein Digitalsignal trägt, unterschiedlich lange Wegstrecken zurücklegt. In einer Glasfaser kann es gleichzeitig mehrere Moden (Wege) der Lichtausbreitung entlang der Faser geben. Digitaldaten, übertragen in Form von Lichtimpulsen, kommen dann zeitlich gestreckt beim Empfänger an. Die gestreckten Lichtimpulse entsprechen elektrischen Impulsen nach Durchlauf durch einen Tiefpass: Ihre Flanken sind flacher geworden und ihre Signalform ist verzerrt. Insgesamt ist die Signalqualität verschlechtert, die Wahrscheinlichkeit eines Bitfehlers steigt.
Jobangebote+ passend zum Thema
Die genaueste Methode, die Hochfrequenztauglichkeit eines Übertragungskanals zu charakterisieren, arbeitet mit einem Messgerät namens „Netzwerkanalysator“. Der Netzwerkanalysator legt ein Sinussignal an den Eingang des Kanals und misst dann das veränderte Sinussignal, das am Ausgang wieder herauskommt. Das Verhältnis Eingangspegel zu Ausgangspegel ist die Dämpfung des Kabels. Man stimmt das Sinussignal über einen großen Frequenzbereich durch und kann so die Dämpfungscharakteristik des Kabels über diesen Frequenzbereich ermitteln.
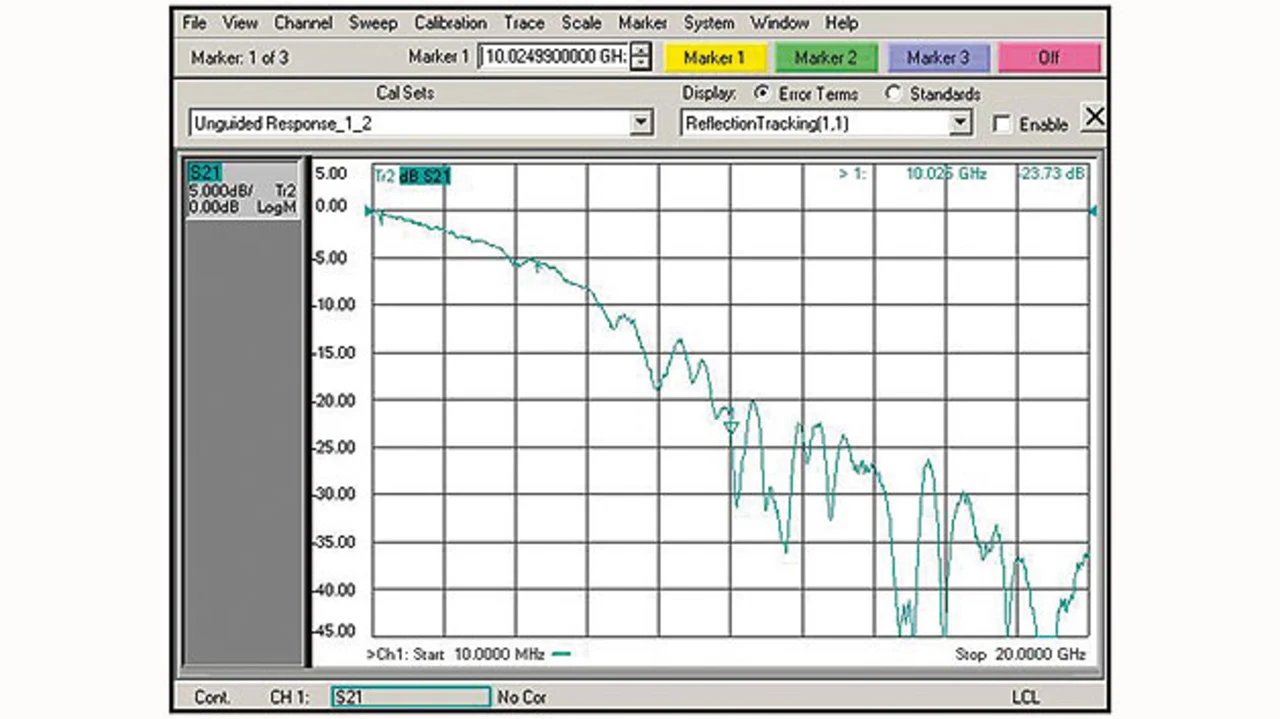
Bild 4 zeigt den Frequenzgang einer 25 cm langen Leiterbahn auf einer Leiterplatte, gemessen mit dem Netzwerkanalysator. Was sagt der Frequenzgang über die Eignung dieser Leiterbahn für ein schnelles Digitalkommunikationssystem aus? Nach der Filtertheorie wirkt die Leitung wie ein Tiefpass: Niedrige Frequenzen gehen fast ohne Verluste durch, hohe Frequenzen aber nur mit entsprechender Dämpfung. Die übertragenen Bits werden beim Durchlauf durch den Kanal verformt. Wie wirkt sich das aus? Man kann diese Frage auf verschiedene Weise angehen. Man kann den Frequenzgang der Leitung mittels inverser Fourrier-Transformation in den Zeitbereich umrechnen und bekommt dann die Impulsantwort des Kanals. Man sieht an ihr, dass ein schmaler Impuls breiter wird und an Amplitude verliert. Ein idealer Impuls hat die Länge 0. Im Frequenzbereich bedeutet das: unendliche Bandbreite. Durchläuft ein solcher idealer Impuls den Kanal, werden seine hohen Frequenzen gedämpft. Am Ausgang des Kanals, zurücktransformiert in den Zeitbereich, ist der Impuls nun breiter und seine Flanken sind nicht mehr so steil. Welchen Einfluss hat das auf die Kommunikationsqualität? Bedenkt man, dass der Pegelunterschied zwischen 0 und 1 nicht groß ist, steigt mit sinkendem Pegel die Wahrscheinlichkeit, dass der Empfänger beim Erkennen des Logikwerts eines Bits einen Fehler macht. Wie wirkt sich die Verbreiterung eines Impulses aus? Ist der Effekt zu groß, überlappt Energie eines Bits die nächste Bitzeit und stört dort. Man nennt dieses Phänomen Symbolübersprechen oder Intersymbol-Interferenz (ISI); sie ist eine weitere Ursache für Bitfehler des Empfängers.
Den Übertragungskanal charakterisieren
In einer solchen Situation liegt es nahe, den Netzwerkanalysator zur Seite zu schieben, einfach ein echtes digitales Kommunikationssignal auf den Kanal zu geben und mit einem Oszilloskop die Qualität der Bits zu beurteilen, die an seinem Ende herauskommen. Das wird auch oft so gemacht. Dennoch ist es üblich, die einzelnen Komponenten eines Kommunikationssystems (nämlich Sender, Übertragungskanal und Empfänger) einzeln zu beurteilen. Das ist schon deswegen sinnvoll, weil die einzelnen Bestandteile manchmal von verschiedenen Herstellern stammen. Die Frequenzgangmessung mit dem Netzwerkanalysator erledigt diese Aufgabe für den Übertragungskanal.
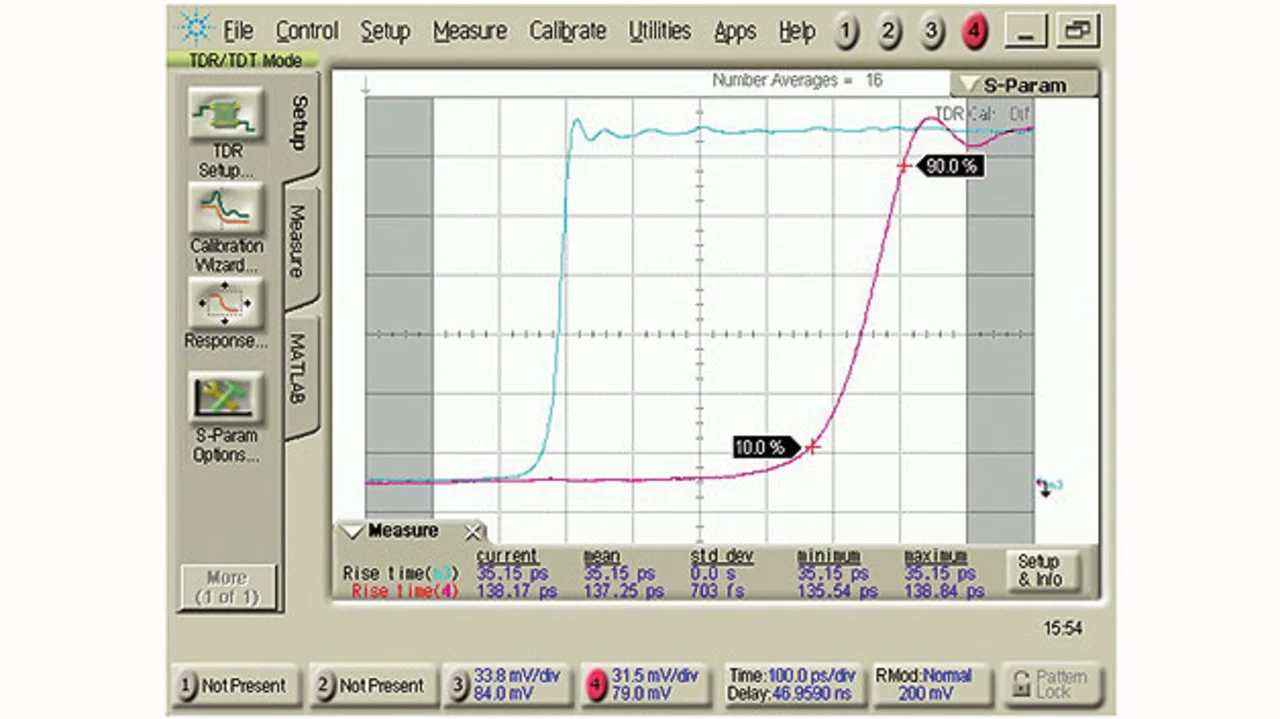
Eine andere, verwandte Methode zur Charakterisierung eines Übertragungskanals besteht darin, einen sehr schnellen Spannungssprung auf den Kanal zu geben und mit einem breitbandigen Oszilloskop zu beobachten, was am anderen Ende herauskommt. Der Vergleich von Eingangssignal und Ausgangssignal zeigt, ob und wie der Kanal digitale Bits beschädigt. Man bezeichnet diese Technik als Zeitbereich-Transmissionsmessung (TDT, Time-Domain Transmission). Bild 5 zeigt eine solche Messung am gleichen Kanal wie in Bild 4. Die blaue Kurve ist das Eingangssignal, die rote zeigt den Spannungssprung, wie er am Ende der Leiterbahn ankommt. (Der Zeitversatz zwischen beiden Kurven wurde verringert, damit man sie leichter vergleichen kann.). Das Bild zeigt zwar nicht die Impuls-antwort des Kanals, sondern die Sprungantwort, die Ergebnisse sind aber ähnlich. Bei einem idealen Übertragungskanal wäre der Sprung am Ausgang deckungsgleich mit dem Sprung am Eingang, er wäre nur entsprechend der Laufzeit im Kanal verzögert. Aber wie bei der Impulsantwort erfahren auch hier die hohen Frequenzen eine Dämpfung, welche die Flankensteilheit verringert. Warum? Das liegt daran, dass für eine steile Flanke hohe Frequenzen nötig sind und diese bei der Übertragung abgeschwächt werden.
Man kann eine TDT-Messung in den Frequenzbereich umrechnen und bekommt dann den Frequenzgang des Kanals. Man kann eine solche mathematische Funktion in ein Oszilloskop einbauen, es liefert dann ein ähnliches Ergebnis wie ein Netzwerkanalysator. Sowohl der Netzwerkanalysator als auch das TDT-Oszilloskop können Messergebnisse sowohl im Zeitbereich als auch im Frequenzbereich liefern, entweder mittels direkter Messung oder mittels Umrechnung. Ein Hochfrequenzingenieur weiß, wie schwierig es ist, die Signalenergie vollständig über einen Kanal vom Sender zum Empfänger zu bringen. Gelingt dies aber nicht vollständig, muss die Restenergie irgendwo hin. Normalerweise wird sie am Empfängereingang reflektiert und läuft dann die Leitung in umgekehrter Richtung zurück. Daraus resultieren zwei Probleme: Wenn am Empfänger weniger Pegel ankommt, steigt die Wahrscheinlichkeit für Empfängerfehler, also die BER. Das zweite Problem besteht darin, dass die reflektierte Energie zum Sender zurückkehrt. Wenn sie dort dann nicht absorbiert wird (etwa weil der Sender dafür nicht ausgelegt wurde), wird das Restsignal dort wieder reflektiert und läuft ein zweites Mal Richtung Empfänger. Der Empfänger sieht nun die Überlagerung von zwei Signalen, die oft einander widersprechen. Ist das Hauptsignal eine Null, wird es durch eine re-reflektierte Geister-Eins verschlechtert; ist es eine Eins, wird eine rereflektierte Geister-Null auch diesen Pegel verschlechtern. In beiden Fällen steigt die Wahrscheinlichkeit für Bitfehler.
- Richtig messen im Zeit- und Frequenzbereich
- Die Bitfehlerrate steigt bei Signalverzerrungen
- Reflexionen informieren über die Anpassung