HF-Messtechnik
Richtig messen im Zeit- und Frequenzbereich
Ingenieure beobachten Signale normalerweise im Zeitbereich. Man kann Signale aber auch als Funktion der Frequenz charakterisieren. Deshalb hier einige Tipps, wie man Signalmessungen im Zeit- und im Frequenzbereich interpretieren sollte.
Je mehr die Digitaltechnik in den Gbit/s-Bereich vorstößt, desto mehr erkennen Digitaltechnik-Ingenieure, dass Messungen im Frequenzbereich wertvolle Einsichten in das Verhalten eines Systems im Zeitbereich eröffnen. HF-/Mikrowelleningenieure andererseits werden mehr und mehr zu Dienstleistern für Digitalanwendungen und müssen dort für Signalintegrität sorgen. Dafür müssen sie Messungen im Zeitbereich beherrschen.
Wichtige Informationen im Zeit- und Frequenzbereich
Wie passt ein HF-Ingenieur besser in die digitale Welt? Wie wird ein Digitalingenieur produktiver, wenn seine Bits im Mikrowellenbereich schwirren? Eine wichtige Fertigkeit lässt beide die Schranke zwischen diesen Welten überwinden und auch im jeweils anderen Bereich erfolgreich sein – nämlich wenn sie lernen, sowohl im Zeitbereich als auch im Frequenzbereich zu denken. Betrachtet man einen digitalen Bitstrom auf einem Oszilloskop und hat eine Vorstellung davon, wie das Spektrum dieses Bitstroms aussieht, gibt dies einen wichtigen Einblick in die Integrität (oder Nicht-Integrität) dieses Signals. Misst man den Frequenzgang oder die Bandbreite eines Kommunikationskanals und hat dabei im Hinterkopf, wie der Bitstrom im Zeitbereich wohl davon beeinflusst wird, kann man erkennen, ob dieser Kanal funktioniert oder nicht.
Jobangebote+ passend zum Thema
Verschiedene Signale im Zeitbereich und ihre Entsprechung im Frequenzbereich.
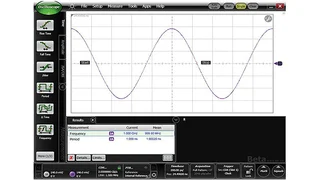
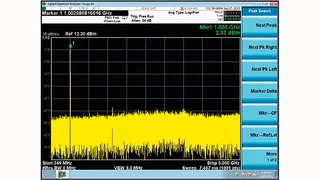
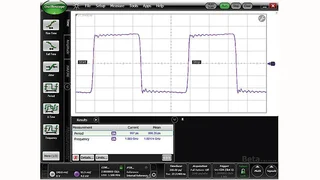
Man kann ein elektrisches Signal als Diagramm – Spannung über der Zeit – darstellen; so betrachtet man ein Signal auf einem Oszilloskop. Man kann das gleiche Signal aber auch als Spektrum – Pegel über Frequenz – anzeigen lassen; so erscheint es auf einem Spektrumanalysator. Mathematisch kann man mittels einer Fourier-Transformation Zeit in Frequenz umrechnen; dieses Verfahren überträgt ein Signal oder eine Funktion vom Zeitbereich in den Frequenzbereich. Es zeigt, welche Teilfrequenzen in einer zeitlichen Messkurve stecken. Einfache Beispiele hierfür sind ein Sinus- und ein Rechtecksignal. Bild 1a zeigt eine Sinuskurve mit einer Periodendauer von 1 ns. Welche Frequenzen stecken in diesem Signal? Dieses Beispiel ist ganz einfach: Das Signal enthält nur eine einzige Frequenz von 1 GHz (siehe Bild 1b). Und wie sieht das mit einem Rechtecksignal mit 1 ns Periodendauer aus? Man würde erwarten, dass es auch eine Frequenz von 1 GHz enthält. Das stimmt auch, aber daneben enthält es noch andere Frequenzen, nämlich 3 GHz, 5 GHz, 7 GHz und so weiter (Bilder 1c und 1d). Das Signal ist zusammengesetzt aus dem Grundton (Kehrwert der Periodendauer) und seinen ungeraden Harmonischen. Mit wachsender Frequenz der Harmonischen sinkt deren Amplitude. Wird die Kurvenform eines Signals im Zeitbereich komplizierter, wird auch das zugehörige Spektrum im Frequenzbereich komplizierter. Das Spektrum eines Digitalsignals mit 2 Gbit/s folgt einer Funktion sin(x)/x. Im Gegensatz zu den obigen Beispielen hat das Signal keinerlei Spektralgehalt bei 2 GHz und den Harmonischen von 2 GHz (Bild 1e und f). Ein Rechtecksignal von 1 GHz entspricht nämlich einem 2-Gbit/s-Signal mit dem Signalinhalt 1-0-1-0-1-0, und beide weisen keine Teilfrequenzen bei geradzahligen Vielfachen von 2 GHz auf.
Wenn das Spektrum eines Signals bekannt ist, also seine Frequenzkomponenten, kann man daraus seine Signalform im Zeitbereich rekonstruieren, also die Kurve Amplitude gegen Zeit. Hierzu benutzt man die inverse Fourier-Transformation. Das funktioniert bei allen Beispielen aus Bild 1; für eine genaue Rekonstruktion braucht man allerdings noch Informationen über die Phasenlage (das ist in Bild 1 nicht dargestellt).
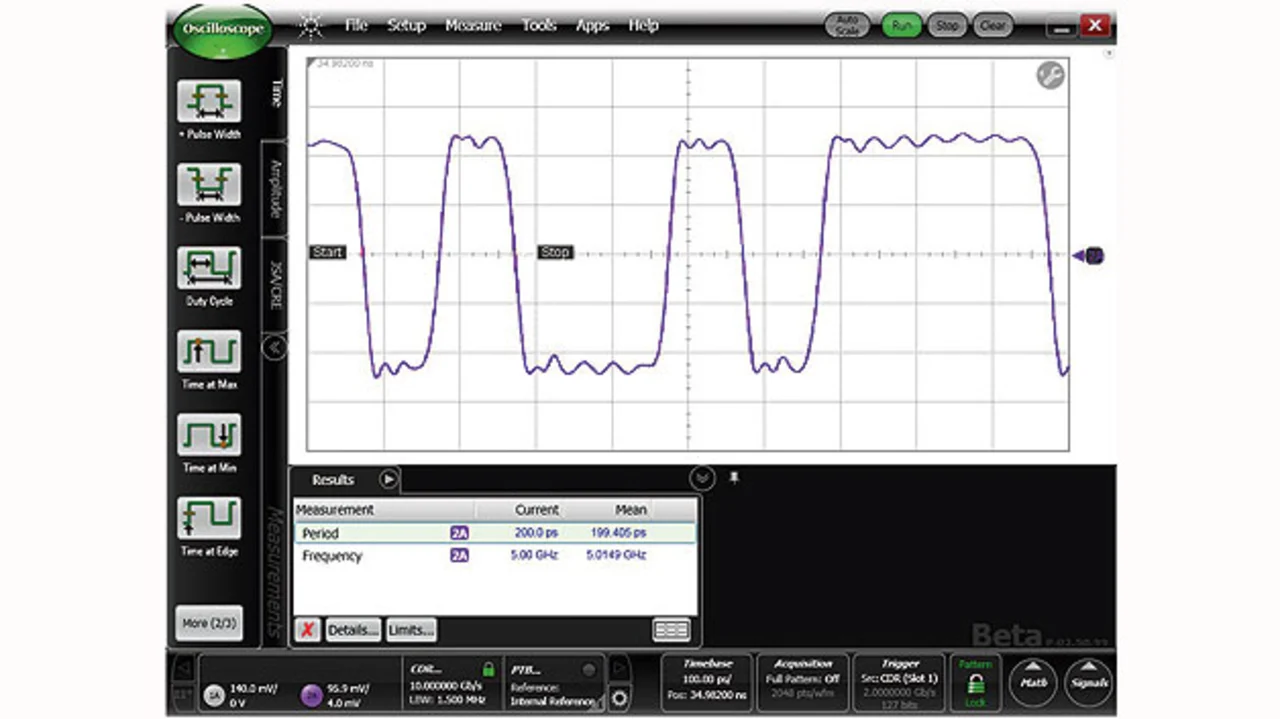
Betrachtet man Digitaldaten auf einem Oszilloskop, würde man eine Folge praktisch rechteckiger Impulse erwarten (die für Einsen stehen) und die Abwesenheit von Impulsen, was für logische Nullen steht. Bei einem schnellen Digitalsignal sieht man das so aber nicht. Die Einsen sind dort längst nicht so rechteckig wie erwartet, und die Nullen sind keine glatten Linien auf Nullniveau. Stattdessen sieht man erheblich geneigte Flanken, die einen Gutteil der Bitzeit in Anspruch nehmen. Wechselt ein Signal von 0 auf 1, schwingt es möglicherweise über, bevor es sich auf dem Nennpegel beruhigt (Bild 2).
Mittels Filtertheorie kann man erklären, warum diese Kurvenformen längst nicht ideal sind. Entwickelt man ein Filter, geht es primär darum, einen bestimmten Frequenzbereich durchzulassen und einen anderen Frequenzbereich zu sperren. Aus dem oben dargestellten Zusammenhang der Kurvenform eines Signals mit seinen Frequenzkomponenten folgt, dass sich die Kurvenform eines Signals vermutlich ändert, wenn es ein Filter durchläuft. Immer, wenn sich das Spektrum eines Signals ändert, ändert sich auch die Kurvenform im Zeitbereich. Was passiert wohl, wenn man das 1-GHz-Rechtecksignal aus Bild 1d durch ein Tiefpassfilter schickt, das Frequenzen bis 2 GHz durchlässt und Frequenzen über 2 GHz sperrt?
Als einzige Frequenzkomponente würde 1 GHz durchgelassen, und aus dem Rechtecksignal würde ein Sinussignal werden. Was würde passieren, wenn das Filter alles bis 4 GHz durchlassen und Frequenzen über 4 GHz sperren würde? Nun würde das Signal hinter dem Filter eine Komponente mit 1 GHz aufweisen und eine mit 3 GHz. Dieses Signal wäre dann zwar keine Sinuskurve, aber auch kein 1-GHz-Rechtecksignal mehr.
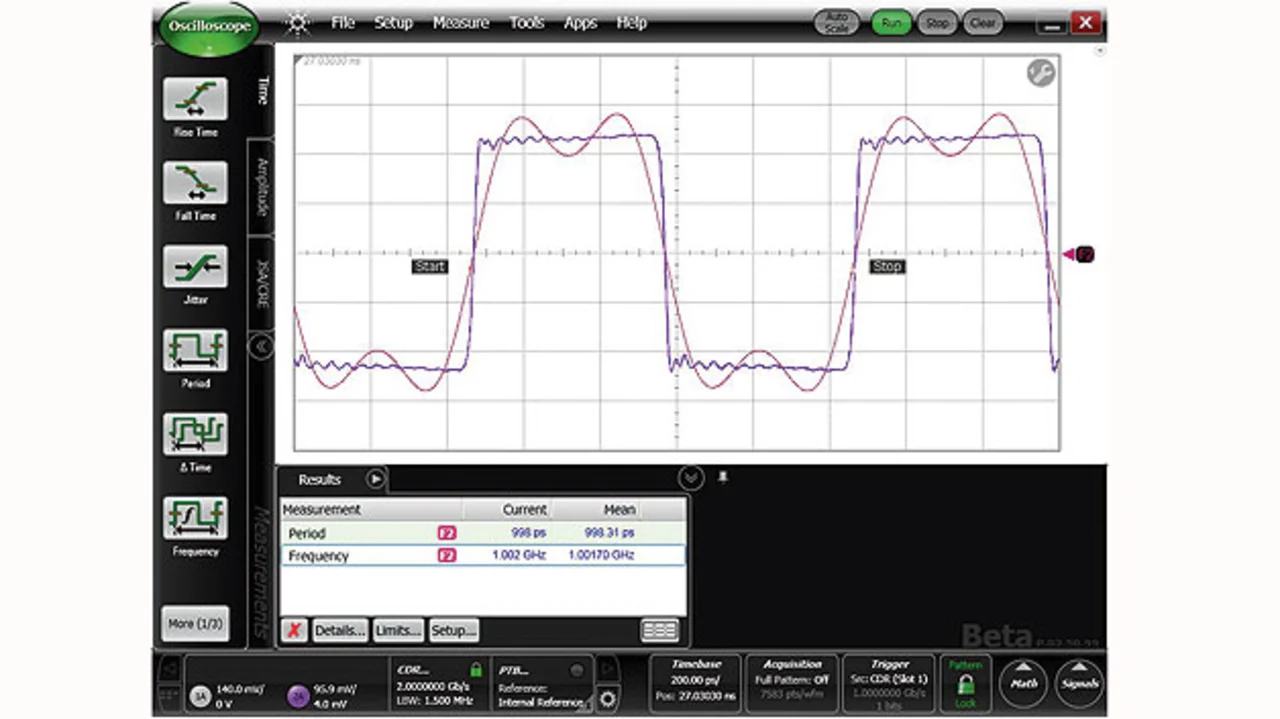
Bild 3 zeigt, was das Tiefpassfilter aus dem Rechtecksignal macht: Die Flanken sind flacher, „Böden“ und „Dächer“ des Rechtecksignals sind nicht mehr eben. Das Signal sieht jetzt aus, als sei eine langsame Sinuskurve (ein 1-GHz-Ton) mit einer schnelleren (einem 3-GHz-Ton) überlagert. Das Filter arbeitet also wie erwartet.
- Richtig messen im Zeit- und Frequenzbereich
- Die Bitfehlerrate steigt bei Signalverzerrungen
- Reflexionen informieren über die Anpassung