Messgenauigkeit in der Leistungsanalyse
Wie genau ist »sehr genau«?
Wer Leistung präzise erfassen will, braucht mehr als nur ein Messgerät mit herausragenden Teilspezifikationen, Mess- und Analysemöglichkeiten. Entscheidend ist auch das Verständnis für die Einflussgrößen auf die Messunsicherheit. Worauf kommt es an? Und wie vermeidet man typische Genauigkeitsfallen?
Wer mit einem Präzisionsmessgerät arbeitet, möchte meist auch wissen, wie genau er damit messen kann. Die zu erwartende Genauigkeit spielt bereits bei der Auswahl eines geeigneten Messgeräts eine große Rolle. Um die Messgenauigkeit zu quantifizieren, müssen die Einflussgrößen bekannt sein und der Bezug zum Messwert hergestellt werden. Das Ergebnis ist die Messunsicherheit – entweder in der physikalischen Einheit des Messwerts oder auch in Prozent vom Messwert. Sie besitzt hohe Aussagekraft und kennzeichnet den Wertebereich für den wahren Wert der Messgröße.
Der Rechenweg zur Messunsicherheit stellt allerdings häufig eine Herausforderung dar. Denn unterschiedliche Gerätekonzepte verschiedener Hersteller erfordern auch unterschiedliche Berechnungen.
Welcher Messbereich bietet die höchste Genauigkeit?
Schon zu Zeiten rein analoger Messtechnik galt: Zu kleine Messwerte lassen sich in einem großen Messbereich nicht ausreichend differenzieren, die Messung wird ungenau. Zu große Messwerte wiederum übersteuern den Messbereich, bringen ein Zeigerinstrument an den Anschlag. Hier gibt es Parallelen zu modernen, digitalen Messgeräten. Allerdings haben Spannungen und Ströme in heutigen Anwendungen häufig hohe Crestfaktoren.
Jobangebote+ passend zum Thema
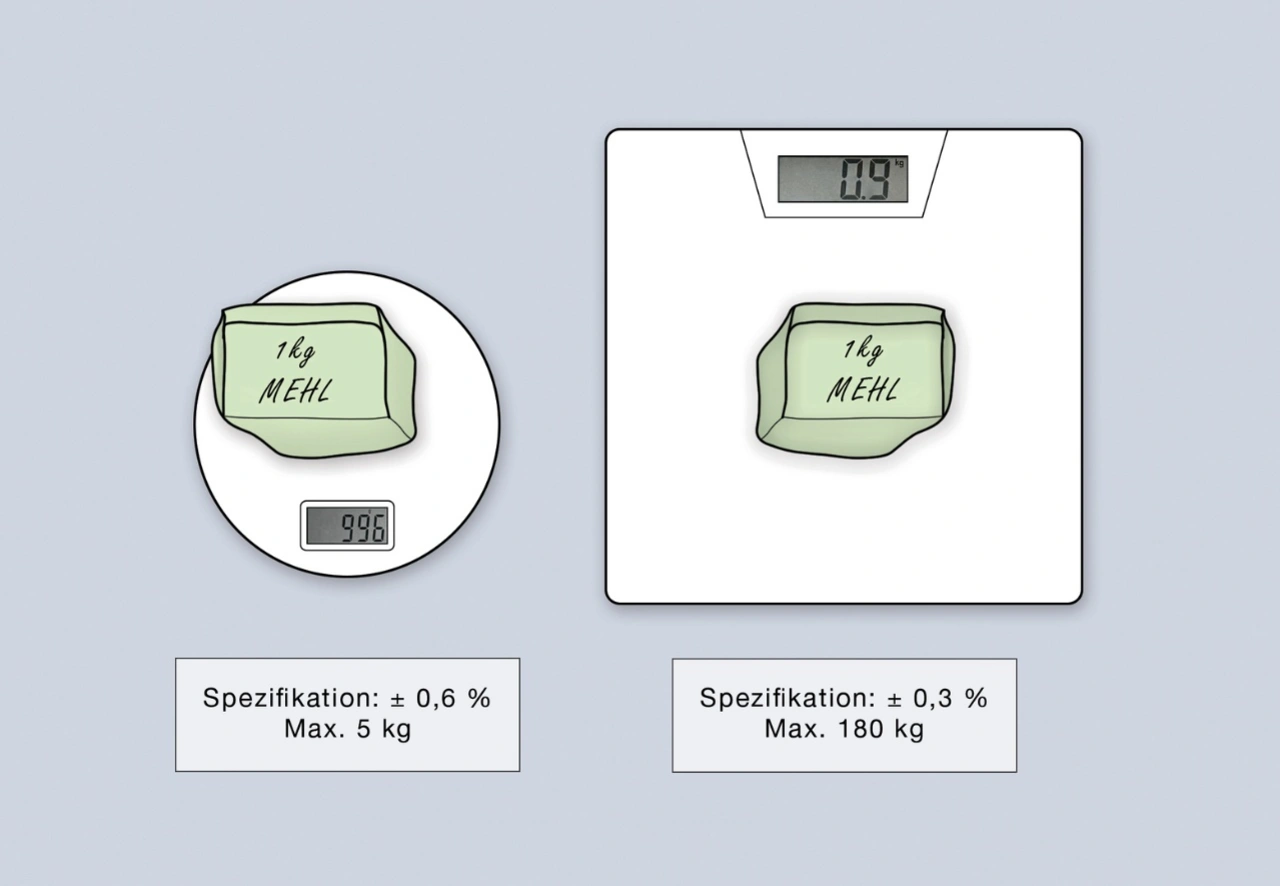
Moderne Messgeräte müssen deshalb sowohl für die zu erwarteten Effektivwerte als auch für die Spitzenwerte der Wechselgrößen geeignet sein. Und auch ein eventueller DC-Anteil ist genau zu messen. Zu hohe Spannungen und Ströme steuern analoge Eingangsschaltungen in den nichtlinearen Bereich. Signalspitzen, die den A/D-Wandler übersteuern, werden abgeschnitten. Sind die Eingangsgrößen jedoch zu klein, kommen störende Einflüsse wie etwa das Quantisierungsrauschen zum Tragen. Auch sie reduzieren die Messgenauigkeit.
Deshalb gilt der Grundsatz, dass sich die Messgenauigkeit mit kleiner werdender Bereichsaussteuerung reduziert, auch bei digital arbeitenden Messgeräten (siehe Bild 1).
Leistungsmessung: Doppelte Relevanz von Bereichseigenschaften
Gehen wir noch einen Schritt weiter und übertragen diese Erkenntnis auf die Leistungsmessung: Dort hat man die Möglichkeit, gleich zweimal günstig oder ungünstig auszusteuern. Weil der Leistungsbereich das Produkt aus Spannungs- und Strombereich ist, führt eine schlechte Aussteuerung sowohl des Spannungs- als auch des Strommessbereichs zu einer sehr schlechten Aussteuerung des Leistungsbereichs. Und das hat entsprechende Konsequenzen für die Genauigkeit der Leistungsmessung.
Bild 2 zeigt das Spezifikationssystem des Präzisions-Leistungsanalysators Yokogawa WT5000 am Beispiel der Messbereiche 300 V, 1 A. Prinzipiell gelten die nachfolgend beschriebenen Zusammenhänge jedoch für alle Bereiche und Bereichskombinationen.
Je nach Messaufgabe stellt man die gewünschten Messbereiche des WT5000 ein oder überlässt dies der automatischen Bereichswahl. Sie berücksichtigt sowohl zulässige Effektiv- als auch zulässige Spitzenwerte. Die Genauigkeit ist für Effektivwerte bis 130 % des Messbereichs spezifiziert. Im 1000-V-Bereich sind sogar 150 % zulässig, sodass Gleichspannungen bis 1500 V gemessen werden können.
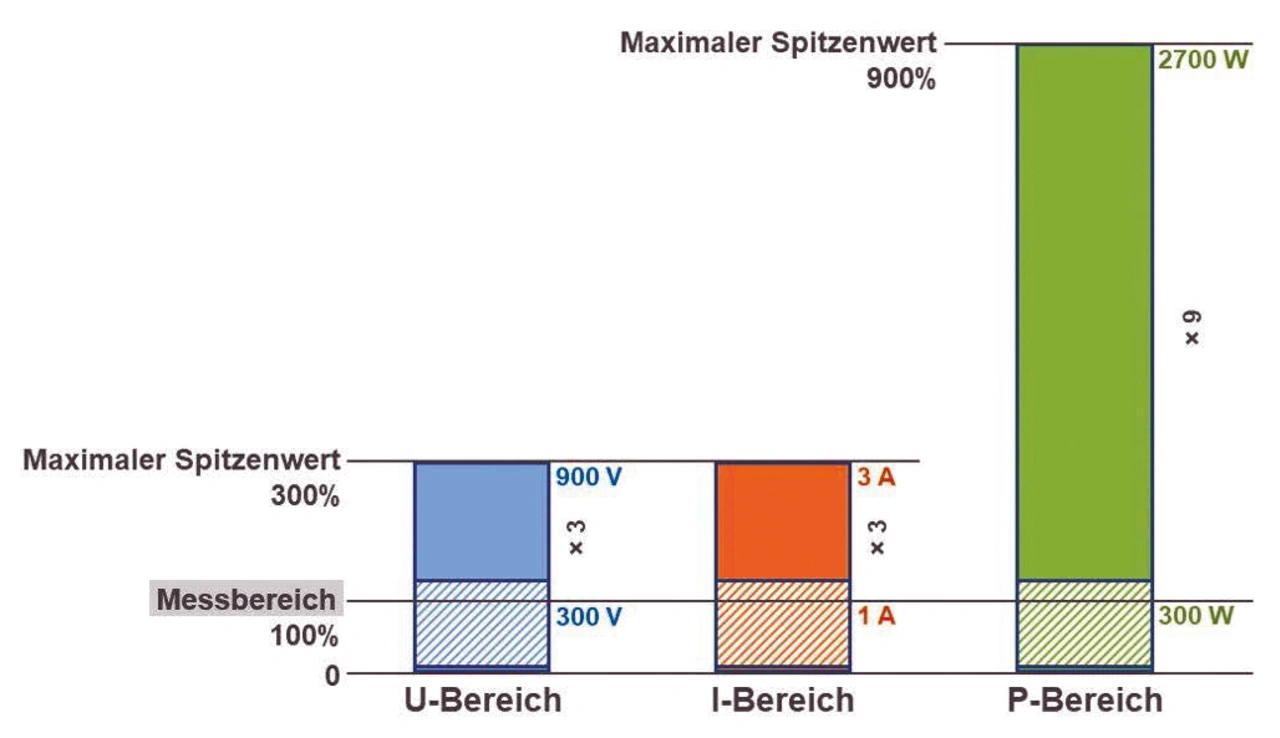
Besonderes Augenmerk gilt aber auch den Spitzenwerten von Wechselspannung und Wechselstrom. Damit sie die Effektivwerte deutlich überschreiten können, dürfen sie 300 % des jeweiligen Messbereichs betragen. Der Bereichs-Crestfaktor (max. Spitzenwert zum Messbereich) des WT5000 ist somit 3. Die untere Grenze für Effektivwerte von Spannungen und Strömen ist für AC 1 % des Messbereichs. Der größtmögliche Signal-Crestfaktor (max. Spitzenwert zum kleinstmöglichen Effektivwert) beträgt deshalb 300.
Bild 2 zeigt beispielhaft einen Leistungsmessbereich von 300 V × 1 A = 300 W. Weil Leistungsmesswerte ebenfalls bis 130 % des Leistungsmessbereichs zulässig sind, ist der größte zulässige Leistungsmesswert 390 W. Die Spitzenwerte (Leistungs-Peaks) dürfen aufgrund der Bereichs-Crestfaktoren der Spannungs- und Strombereiche sogar 2700 W betragen.
Für Genauigkeitsberechnungen sind diese zulässigen Spitzenwerte nicht relevant. Denn Genauigkeitsspezifikationen gelten für sinusförmige Spannungen und Ströme, die einen Signal-Crestfaktor von nur √2 aufweisen. Sind jedoch zusätzliche Frequenzen im Spiel, erhöhen sich die Spitzenwerte – und mit ihnen auch die Signal-Crestfaktoren.
Die Berechnung der Crestfaktoren ist wie folgt:
- Signal-Crestfaktor einer Spannung oder eines Stroms: Spitzenwert dividiert durch den Effektivwert
- Bereichs-Crestfaktor eines Spannungs- oder Strombereichs: Maximaler Spitzenwert dividiert durch den Nennwert des Bereichs
Wie entsteht Wirkleistung? Welchen Einfluss haben hohe Spitzenwerte von Spannung und Strom?
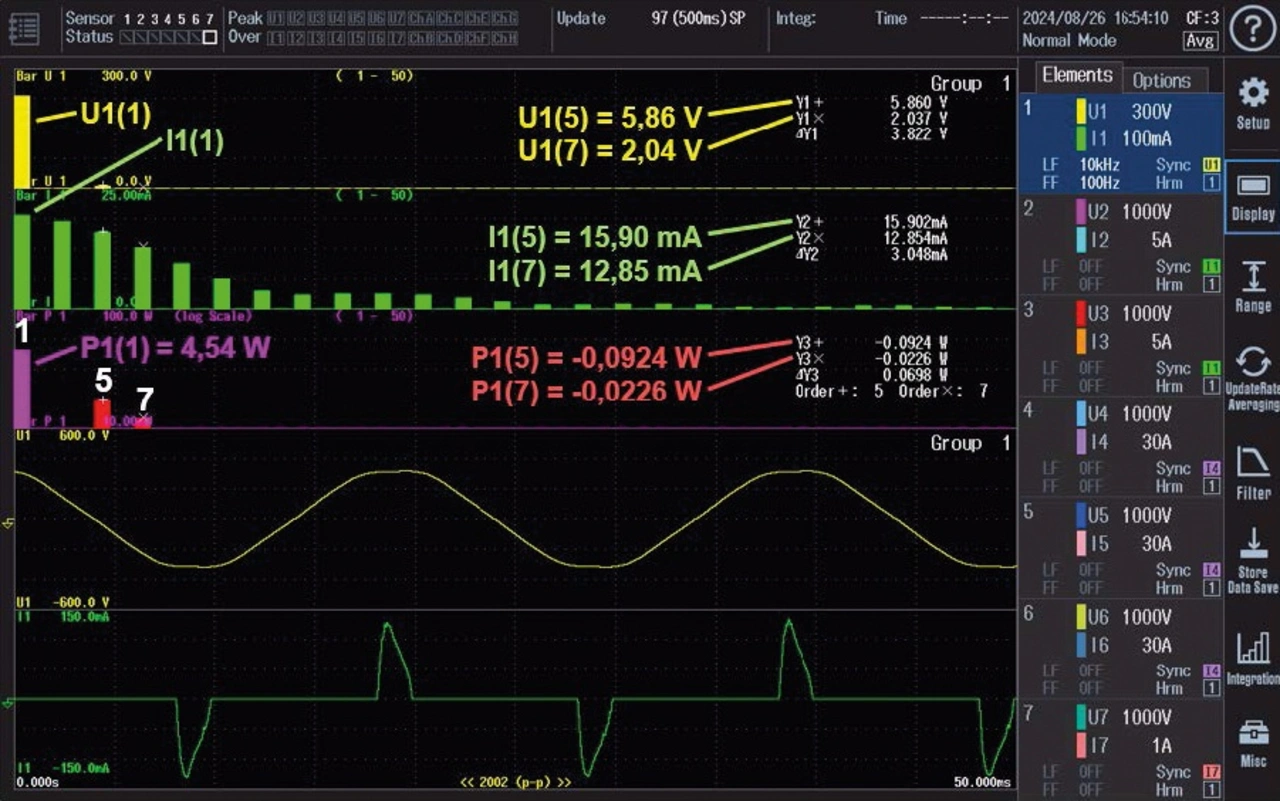
Um diese Fragen zu beantworten, schauen wir auf Bild 3. Es zeigt die Kurvenformen von Spannung und Strom sowie das Frequenzspektrum am Eingang eines USB-Netzteils.
Im Leistungsspektrum ist Wirkleistung bei den Ordnungszahlen 1, 5 und 7 zu sehen. Bei Ordnungszahl 1 (also 50 Hz) sind es 4,54 W. Hier befinden sich erwartungsgemäß die größten Effektivwerte von Spannung und Strom. Darüber hinaus gibt es kleine Spannungen bei Ordnungszahlen 5 und 7, die mit den Cursoren »+« und »×« markiert sind. Im Zusammenspiel mit den Strömen bei identischen Ordnungszahlen 5 und 7 leisten sie einen geringen Beitrag zur Gesamtleistung. Er lässt sich in gewohnter Art und Weise für jede Ordnungszahl k berechnen, hier für Leistungselement Nummer 1:
P1(k) = U1(k) × I1(k) × cosΦ1(k)
Bei jeder Ordnungszahl k bestehen sinusförmige Verhältnisse, und die Amplituden von U1(k) sowie I1(k) werden durch ihre Effektivwerte eindeutig beschrieben. Größe und Richtung der Wirkleistungsbeiträge P1(k) sind darüber hinaus vom jeweiligen Phasenwinkel Φ1(k) beziehungsweise dem Leistungsfaktor cosΦ1(k) abhängig.
Diese Erkenntnisse lassen sich wie folgt zusammenfassen: Auch bei Frequenzgemischen sind die Effektivwerte für das Vorhandensein von Wirkleistung maßgeblich. Oberschwingungen im Stromspektrum erhöhen die Spitzenwerte des Stromverlaufs. Wenn es für die Oberschwingungen auch ein gleichfrequentes Pendant auf der Spannungsseite gibt, dann leisten sie auch einen Beitrag zur Wirkleistung.
Grundsätzlich sind auch die Spitzenwerte bei der Bereichswahl zu berücksichtigen, denn durch ein Abschneiden der Spitzen (Clipping) würde der digitalisierte Kurvenverlauf nicht mehr der ursprünglichen Kurvenform entsprechen. Das hätte Einfluss auf das Frequenzspektrum, auf die Effektivwerte von Spannung und Strom sowie die gemessene Wirkleistung.
Wie wird die Leistungsmessgenauigkeit spezifiziert?
Aus physikalischer Sicht gibt es vielfältige Einflussgrößen. Das gilt insbesondere in der Präzisions-Leistungsmesstechnik. Die kommt zum Einsatz, wenn die Anforderungen an die Genauigkeit sehr hoch sind und auch geringste Abweichungen eine Rolle spielen. Um die Einflüsse zu beschreiben, ordnet man sie nach Möglichkeit dem Messbereich oder dem Messwert zu.
Ein Beispiel: Ein A/D-Wandler wird keine 300 V direkt verarbeiten. Gehen wir deshalb davon aus, dass ein Spannungsteiler die zu messenden 300 V für den Eingang des A/D-Wandlers reduziert. Auch bei höchster Präzision wird das Teilerverhältnis minimal vom idealen Teilerverhältnis abweichen und so einen Beitrag zur Unsicherheit des Spannungsmesswerts leisten. Weil dies gleichermaßen kleine und große Messwerte betrifft quantifiziert man diesen Effekt mit »% vom Messwert«.
Ein anderes Beispiel: Minimale Rauschanteile (thermisches Rauschen, Halbleiterrauschen, Quantisierungsrauschen) sind immer vorhanden und überlagern die zu messende Größe. Geht man von einem konstanten Rauschanteil aus, macht es Sinn, diesen in »% vom Messbereich« zu spezifizieren. Das bringt zum Ausdruck, dass das Rauschen mit kleiner werdender Bereichsaussteuerung an Bedeutung gewinnt.
Messunsicherheitsbeiträge, die sich entweder dem Messwert oder dem Messbereich zuordnen lassen, werden somit in nachfolgender Formel zusammengefasst:
Messunsicherheit = ±(x % vom Messwert + y % vom Messbereich)
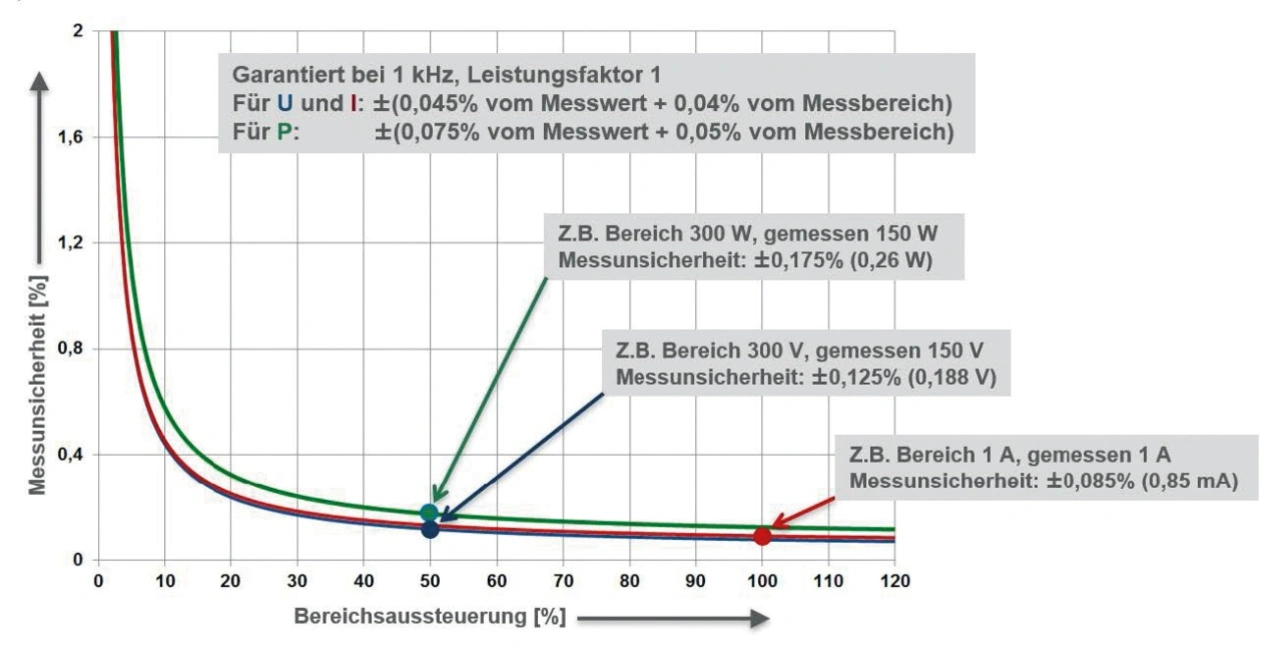
Bild 4 zeigt, wie sich die Größe des Messwerts (dargestellt in % des Messbereichs) auf die Messunsicherheit auswirkt. Sie basiert auf den Garantiewerten des WT5000 für 1 kHz.
Die hohe Messgenauigkeit ändert sich über einen weiten Bereich der Aussteuerung nur wenig. Dafür sorgt der geringe Beitrag »y % vom Messbereich«. Nur wenn dieser Anteil klein ist, sind auch genaue Messungen bei kleinen Bereichsaussteuerungen möglich. Typischerweise werden diese Garantiewerte deutlich übertroffen, sodass auch bei Bereichsaussteuerungen von 1 % hohe Genauigkeiten erzielt werden können.
Nennwert- oder Spitzenwert-basierende Bereiche
Zu Zeiten rein analoger Messtechnik war die Definition der Bereiche sehr einfach und eindeutig. Wenn der 250-V-Bereich eines Spannungsmessgerätes eingestellt wurde, betrug auch der Skalenendwert 250 V und man konnte Effektivwerte bis 250 V messen. Bei modernen, digitalen Messgeräten sind jedoch bis zu vier Bereichsangaben zu differenzieren. Es gibt:
- den eingestellten Messbereich (also den Nennwert)
- den Bereich, innerhalb dessen die Genauigkeitsspezifikationen gelten (z.B. Effektivwerte von 1 % bis 130 % des eingestellten Messbereichs)
- den Bereich, innerhalb dessen noch Messwerte angezeigt werden (z. B. Effektivwerte bis 140 % des eingestellten Messbereichs)
- die Spitzenaussteuerbarkeit des Bereichs. Das ist die Obergrenze, bei der Signalspitzen noch nicht abgeschnitten werden. Andere gängige Begriffe hierfür sind »Messbereichsendwert«, »Maximum Peak Value« und »Full Scale«.
Es gibt allerdings auch digitale Messgeräte mit nur einer Bereichsangabe. Dann sind Messbereich und die Obergrenze für Signalspitzen identisch. Infolgedessen ist der maximal messbare Effektivwert eines Sinus mit seinem Crestfaktor von √2 etwa 30 % kleiner als der eingestellte Messbereich.
Weitere Gerätekonzepte differenzieren zwischen Messbereich und Spitzenaussteuerbarkeit, nehmen jedoch mit »y % vom Messbereichsendwert« auf die erlaubten Obergrenzen für Signalspitzen Bezug. Hohe Bereichs-Crestfaktoren der Spannungs- und Strombereiche stehen in diesen Fällen für kleine Prozentwerte. Auch für Leistungsbereiche ist ein Bezug auf Messbereichsendwerte gängige Praxis. Dann multiplizieren sich die Effekte hoher Bereichs-Crestfaktoren der Spannungs- und Strombereiche.
Fallbeispiele im Vergleich: Drei Geräte, drei Genauigkeiten
Hier drei Beispiele für die Berechnung der Genauigkeit einer Leistungsmessung bei 150 W, 1 kHz, 200 V, 750 mA, Leistungsfaktor 1:
A) Präzisions-Leistungsanalysator Yokogawa WT5000
Im Präzisions-Leistungsanalysator Yokogawa WT5000 wird ein Spannungsbereich von 300 V und ein Strombereich von 1 A eingestellt. Die zugehörigen Messbereichsendwerte sind 900 V und 3 A. Daraus ergibt sich ein Leistungsbereich mit einem Nennwert von 300 W und einem Messbereichsendwert von 2700 W.
Die Genauigkeit der Leistungsmessung ist spezifiziert mit ±(0,075 % vom Messwert + 0,05 % vom Messbereich). Somit ist die Messunsicherheit: ±0,26 W oder ±0,175 % vom Messwert.
B) Leistungsanalysator (Messbereich = Obergrenze für Signalspitzen)
Der Leistungsanalysator verfügt über einen Spannungsbereich von 500 V und einen Strombereich von 3 A. Die Bereichsangaben sind gleichzeitig auch die Messbereichsendwerte. Daraus ergibt sich ein Leistungsbereich von 500 V × 3 A = 1500 W, der sowohl den Nennwert als auch den Messbereichsendwert darstellt.
Die Genauigkeit der Leistungsmessung sei spezifiziert mit ±(0,075 % vom Messwert + 0,05 % vom Messbereich). Somit ist die Messunsicherheit: ±0,86 W oder ±0,575 % vom Messwert.
Der Vergleich mit A:
- Die Spezifikation ±(0,075 % vom Messwert + 0,05 % vom Messbereich) ist identisch
- Leistungsanalysator B) kann größere AC Leistungen (500 V/√2 × 3 A/√2 = 750 W) messen, jedoch keine so großen Leistungsspitzen wie A).
- In dieser Messaufgabe ist die Messunsicherheit des Leistungsanalysators B) 3,3 mal so groß wie bei A)
C) Präzisions-Leistungsanalysator mit Messbereichsendwertdefinition
Das Messgerät verfügt über einen Spannungsbereich von 250 V und einen Strombereich von 1,2 A. Die zugehörigen Messbereichsendwerte sind 400 V und 3,75 A. Daraus ergibt sich ein Leistungsbereich mit einem Nennwert von 300 W und einem Messbereichsendwert von 1500 W.
Die Genauigkeit der Leistungsmessung sei spezifiziert mit ±(0,024 % vom Messwert + 0,03 % vom Messbereichsendwert). Somit ist die Messunsicherheit: ±0,49 W oder ±0,324 % vom Messwert.
Der Vergleich mit A):
- Die Nennwerte der Leistungsbereiche sind in beiden Fällen identisch.
- Die Spitzenaussteuerbarkeit des Leistungsbereichs ist bei C) deutlich kleiner als bei A).
- Die Messunsicherheit ist bei C) 1,9 mal so groß wie bei A).
- Der Bereichseinfluss ist aufgrund des viel größeren Bezugswertes (1500 W anstatt 300 W) trotz kleinem Prozentwert groß und dominiert die Messunsicherheit.
Die Ergebnisse der Vergleiche auf den Punkt gebracht:
- Genauigkeitsspezifikationen kann man erst beurteilen, wenn man das dahinterstehende Spezifikationssystem kennt und entsprechend rechnet. Erst der Bezug auf den Messwert hat Aussagekraft.
- Genauigkeitsspezifikationen gelten für sinusförmige Spannungen und Ströme, deren Crest-Faktor mit √2 klein ist. Weitaus häufiger sind jedoch Frequenzgemische zu messen. Deshalb ist ergänzend zu bewerten, welche Dynamik die Messbereiche sowohl für Effektivwerte als auch für Spitzenwerte bieten.
- Wenn hohe Effektiv- oder Spitzenwerte eine Umschaltung in den nächstgrößeren Bereich erfordern, so fällt das Ergebnis der Messunsicherheitsberechnung zwangsläufig ungünstiger aus. Deshalb ist auch von Bedeutung, ob ein Leistungsanalysator die zur Messaufgabe passenden Messbereiche bietet.
| Absolut () | Relativ, bezogen auf den Messwert | |
|---|---|---|
| (a) Messwertkomponente | x % vom Messwert | x % |
| (b) Messbereichskomponente | y % vom Messbereich x cosϕ | (y Messbereich/Messwert x cosϕ) % |
| (c) Einfluss des Leistungsfaktors | z % vom Messwert x tanϕ | (z x tanϕ) % |
Tabelle 1: Die Umrechnung der Messbereichskomponente (kursiv) stellt den prozentualen Bezug zum Messwert her
Meist unterschätzt: Der Einfluss des Leistungsfaktors auf die Messgenauigkeit
Bisher wurde die Leistungsmessgenauigkeit bei Leistungsfaktor 1 betrachtet. Die Komponente »y % vom Messbereich« lässt die Messunsicherheit mit kleiner werdenden Messwerten prozentual ansteigen. Doch wie sind die Zusammenhänge, wenn Spannungen und Ströme ihre Bereiche hervorragend aussteuern, die Leistung jedoch aufgrund des Leistungsfaktors klein wird?
Dann geraten Bereichseinflüsse wie das Quantisierungsrauschen in den Hintergrund. Der Zusammenhang lässt sich sehr einfach abbilden, indem die Bereichskomponente um den Leistungsfaktor ergänzt wird. Aus »y % vom Messbereich« wird somit »y % vom Messbereich × cosΦ«. Und in gleichem Maße, wie der Leistungsfaktor den Wirkleistungsmesswert reduziert, verlieren die Bereichseinflüsse an Bedeutung.
Stattdessen kommt jedoch der nachfolgend beschriebene Einfluss durch eventuelle Phasenwinkelabweichungen zum Tragen.
Die Formel P = U × I × cosΦ = S × cosΦ zeigt, dass die Wirkleistung P bei konstanter Scheinleistung vom Leistungsfaktor cosΦ abhängig ist. Ändert sich der Phasenwinkel Φ aufgrund von Phasendifferenzen zwischen Spannungs- und Strompfad eines Leistungsanalysators, ändert sich auch der Leistungsmesswert.
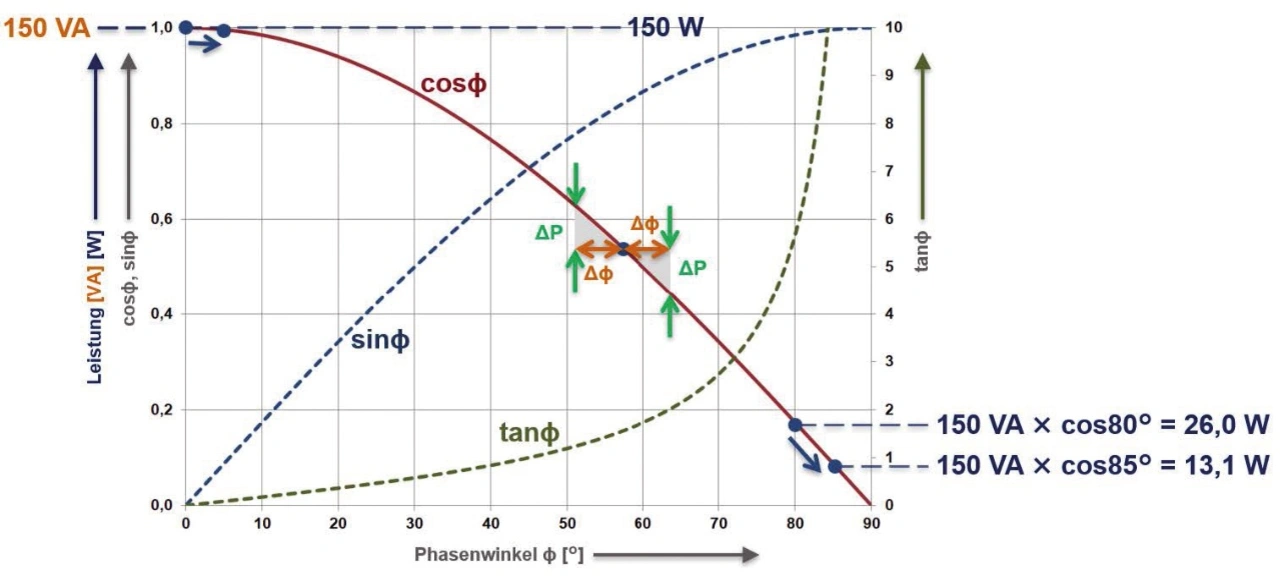
Bild 5 beschreibt diese Zusammenhänge. Die rote Funktion stellt den Kosinus von 0 bis 90° dar. Bei einem Phasenwinkel von 0° ist der Kosinus 1 und die Wirkleistung so groß wie die Scheinleistung. Je weiter sich der Phasenwinkel in Richtung 90° bewegt, desto kleiner wird der Kosinus und damit auch die Wirkleistung. Darüber hinaus ändert sich aber auch die Steilheit des Kosinus. Deshalb hat eine Änderung des Phasenwinkels nahe 90° einen viel größeren Einfluss als bei Phasenwinkeln nahe 0°. Entscheidend für die Abweichung eines Leistungsmesswerts ist somit nicht nur die Phasenwinkeländerung, sondern auch der Phasenwinkel (oder Leistungsfaktor) im aktuellen Betriebspunkt des Messobjekts. Aus diesem Grund wird dieser Zusammenhang bei Präzisions-Leistungsanalysatoren wie WT5000 als »Einfluss des Leistungsfaktors« beschrieben.
In Bild 5 ist die Wirkleistung bei einem Phasenwinkel von 0° (Leistungsfaktor 1) 150 W. Darauf hätte sogar eine Winkeländerung von 5° kaum Einfluss. Geschieht diese Winkeländerung jedoch bei einem Phasenwinkel von 80° (Leistungsfaktor 0,174), so ist der Einfluss auf den nun ohnehin kleinen Leistungsmesswert von 26 W enorm.
Sind so große Winkelabweichungen überhaupt möglich? Es kommt auf die Frequenz an. Bei 50 Hz: Nein. Bei 250 kHz: Ja. Ein ganz einfaches Rechenexempel verdeutlicht dies: Ein Laufzeitunterschied von nur 56 ns zwischen Spannungs- und Strompfad würde den Phasenwinkel bei 250 kHz um 5° verändern. Bei 50 Hz wären es nur 0,001°. Und die wären auch bei einem Phasenwinkel von 80° unbedeutend.
Grundsätzlich ist mit zunehmenden Frequenzen auch mit zunehmenden Phasenwinkelabweichungen zu rechnen, während die bei hohen Frequenzen meist kleiner werdenden Leistungsfaktoren den Einfluss des Leistungsfaktors zusätzlich begünstigen. Trotz der Paarung von Spannungs- und Stromeingängen ist es auch bei Präzisions-Leistungsanalysatoren nicht möglich, ihn zu eliminieren.
Wie lässt sich der Einfluss des Leistungsfaktors auf die Messgenauigkeit mathematisch fassen?
In Bild 5 ist die maximal mögliche Phasenwinkelabweichung ΔΦ zwischen Spannungs- und Strompfad eines Leistungsanalysators bei einem Phasenwinkel von Φ = 57,3° eingezeichnet. Sie ist eine Eigenschaft des Leistungsanalysators und somit unabhängig davon, bei welchem Phasenwinkel (Leistungsfaktor) gerade gemessen wird. Die daraus resultierende Wirkleistungsänderung ΔP ist es allerdings nicht. Wird der Phasenwinkel Φ kleiner, so wird auch ΔP kleiner. Wird der Phasenwinkel größer, so gilt das auch für ΔP. Dieser Zusammenhang wird durch die blau gestrichelte Sinus-Funktion exakt abgebildet. Bei 90° entspricht ΔP dem gerade noch zulässigen, geringen Leistungsmesswert bei Leistungsfaktor 0.
In einem weiteren Schritt bietet es sich an, die Wirkleistungsänderung ΔP in Bezug zur Wirkleistung P zu setzen. Mit sinΦ als Maß für ΔP und cosΦ als Maß für P wird deutlich, dass der Einfluss des Leistungsfaktors mit der Tangens-Funktion beschrieben werden kann. Denn sinΦ dividiert durch cosΦ ergibt tanΦ. Deshalb stellt die grün gestrichelte Tangens-Funktion im Bild 5 den Zusammenhang zwischen dem Leistungsfaktor und dessen maximal möglichen Einfluss auf den Wirkleistungsmesswert aufgrund von Phasenwinkelabweichungen dar. Der dramatische Anstieg des Tangens bei Phasenwinkeln oberhalb 80° verdeutlicht, warum Leistungsmessungen an stark induktiven oder kapazitiven Verbrauchern besonders herausfordernd sind. Je weiter sich der Phasenwinkel auf 90° zubewegt, desto stärker fallen auch kleinste Phasenwinkelabweichung ins Gewicht.
Die Berechnung der Leistungsmessgenauigkeit ist bei Yokogawa-Leistungsanalysatoren für alle Kombinationen aus Spannungs- und Strombereichen gleich. Tabelle 1 fasst die beschriebenen Einflüsse zusammen. Die Werte für x, y und z sind frequenzabhängig und können den Gerätespezifikationen entnommen werden. Darüber hinaus gibt es weitere Einflüsse auf die Messgenauigkeit, die hier nur erwähnt werden sollen. Darunter fallen die Betriebsbedingungen (Temperatur, Luftfeuchte), die Eigenerwärmung des Shunts aufgrund des Stromflusses, Amplituden- und Phasenänderungen durch externe Stromwandler.

Was ist die Grundgenauigkeit eines Leistungsanalysators?
Für den Begriff »Grundgenauigkeit« gibt es keine allgemeingültige, anerkannte Definition. Treffender wäre deshalb die Frage, was darunter verstanden wird.
Aus Anwendersicht besteht der naheliegende Wunsch einer einfachen Klassifizierung der Messgenauigkeiten unterschiedlicher Leistungsanalysatoren. Im Umkehrschluss haben Messgerätehersteller ein Interesse daran, sich mit einer Grundgenauigkeitsangabe positiv zu positionieren. Ein Vergleich der Grundgenauigkeiten verschiedener Leistungsanalysatoren zeigt jedoch, dass sie für eine belastbare Klassifizierung ungeeignet sind.
Eine Einordnung
Leistungsanalysatoren sind meist für Netzfrequenzen optimiert. Weil die Hauptaufgabe eines Leistungsanalysators die Wirkleistungsmessung ist, sollte sie bei der Spezifikation einer Grundgenauigkeit im Vordergrund stehen. Insofern kann eine Grundgenauigkeitsangabe für die bestmögliche Leistungsmessgenauigkeit bei Netzfrequenz stehen.
Es sind allerdings auch Grundgenauigkeitsangaben zu finden, die sich bei genauer Betrachtung auf die Messung von Spannung oder Strom beziehen.
Wird die Grundgenauigkeit als ein einzelner Prozentwert ohne weitere Erklärung dargestellt, so kann damit »x % vom Messwert«, »y % vom Messbereich« oder die Summe aus beiden gemeint sein. Sofern Unklarheit darüber besteht, hilft meist ein kurzer Blick in die ausführliche Herstellerspezifikation.
Die einfache Summe »x % + y %« kommt der bestmöglichen Messgenauigkeit am nächsten. Voraussetzung dafür ist allerdings, dass die Bezugsgrößen »Messwert« und »Messbereich« gleich groß sind. Das ist beispielsweise bei Yokogawa-Leistungsanalysatoren der Fall, wenn 300 W im Leistungsbereich 300 W gemessen werden. Dann ist die Bereichsaussteuerung 100 %.
Wäre der Bezug für »y %« jedoch der Messbereichsendwert von 1500 W aus Beispiel »C) Präzisions-Leistungsanalysator mit Messbereichsendwertdefinition«, so könnte die Bedingung gleicher Bezugsgrößen nie erfüllt werden. Denn hier sind Leistungsspitzen bis 1500 W zulässig, maximale Leistungsmesswerte aufgrund des Leistungsbereichs mit dem Nennwert 300 W jedoch deutlich kleiner. Aufgrund der unterschiedlichen Bezugsgrößen wäre die einfache Summenbildung »x % + y %« mathematisch inkorrekt und hätte gar keine Aussagekraft.
Der korrekte Bezug auf einen Messwert bei 100 % Bereichsaussteuerung (also 300 W) ließe sich jedoch auch hier einfach herstellen. Dazu wäre die Bereichskomponente »y %« lediglich mit dem Faktor »(Messbereichsendwert/Messbereich) = 5« zu multiplizieren.
Auch in diesem Fall könnte ein kurzer Blick in die Herstellerspezifikation eventuelle Unklarheiten sehr einfach ausräumen.
Fazit: Genau messen beginnt mit genauem Hinschauen
Doch auch die »bestmögliche Messgenauigkeit« bei 100 % Aussteuerung eines Leistungsbereichs ist nur bedingt praxisgerecht, denn eine hohe Messgenauigkeit bei 100 % Bereichsaussteuerung ist nicht besonders herausfordernd. Und für genaue Leistungsmessungen bei kleinen Bereichsaussteuerungen ist von entscheidender Bedeutung, wie sich die Prozentwerte auf die Messwert- und Bereichskomponente verteilen.
Das lässt sich anschaulich anhand der Messaufgabe an einem Antriebssystem aufzeigen. Aufgrund der Spitzenwerte der pulsweiten modulierten Ausgangsspannung eines Umrichters ist der erforderliche Spannungsmessbereich in der Regel groß. Das gilt auch dann, wenn der Umrichter für den aktuellen Arbeitspunkt nur eine kleine Spannungskomponente bei Betriebsfrequenz liefert. Weil die vom Motor aufgenommene Wirkleistung hauptsächlich durch Spannung und Strom bei Betriebsfrequenz gebildet wird, ist die Aussteuerung des Leistungsbereichs gering. Anforderungen an hohe Messgenauigkeiten lassen sich hier nur erfüllen, wenn Leistungsanalysatoren auch bei kleinen Bereichsausteuerungen belastbare Leistungsmesswerte liefern. Bei Yokogawa WT5000 ist das bei Bereichsaussteuerungen ab 1 % garantiert.