Wie gut sind SPICE-Modelle für OPVs?
Ausgangsimpedanz im Leerlauf unter der Lupe
Haben sie je hinterfragt, ob das SPICE-Modell des gewählten Operationsverstärkers auch mit den Datenblatt-Spezifikationen übereinstimmt? Teil fünf der Serie widmet sich den Kleinsignal-Eigenschaften von SPICE-Modellen und wie OPV-Modelle dahingehend getestet werden können.
Instabiles Verhalten von Verstärkerstufen kann sich durch Überschwinger ebenso äußern wie durch kurzzeitiges Schwingen, dauerhafte Oszillationen oder anderes bizarres Verhalten. Verhält sich eine Verstärkerschaltung instabil, kann es äußerst schwierig werden, die Ursache zu beheben.
Glücklicherweise gibt es mit dem SPICE-Modell ein wertvolles Hilfsmittel im Kampf gegen Stabilitätsprobleme von Operationsverstärkern. Ein gutes Modell kann zusammen mit den in der Simulation verfügbaren, leistungsfähigen Analysewerkzeugen dabei helfen, das Verhalten von Operationsverstärkerschaltungen vorherzusagen und sie zu stabilisieren, bevor sie im realen Einsatz Probleme verursachen.
Es gibt zwar eine Vielzahl verschiedener Stabilitäts-Kompensationsmethoden, doch würde eine fundierte Abhandlung hierzu den Rahmen dieses Beitrags sprengen. Stattdessen will ich mich auf die Beantwortung der Frage beschränken, wie sich verifizieren lässt, dass das SPICE-Modell eines Operationsverstärkers präzise genug für die Verwendung in der Stabilitätsanalyse ist. Hierzu wird das Verhalten des Modells mit dem Datenblatt verglichen. Wenn Sie sich genauer mit der Theorie der Stabilität von Operationsverstärkern und den entsprechenden Kompensationstechniken befassen möchten, empfehle ich als Start die Videoserie [22].
Jobangebote+ passend zum Thema
Leerlauf-Ausgangsimpedanz
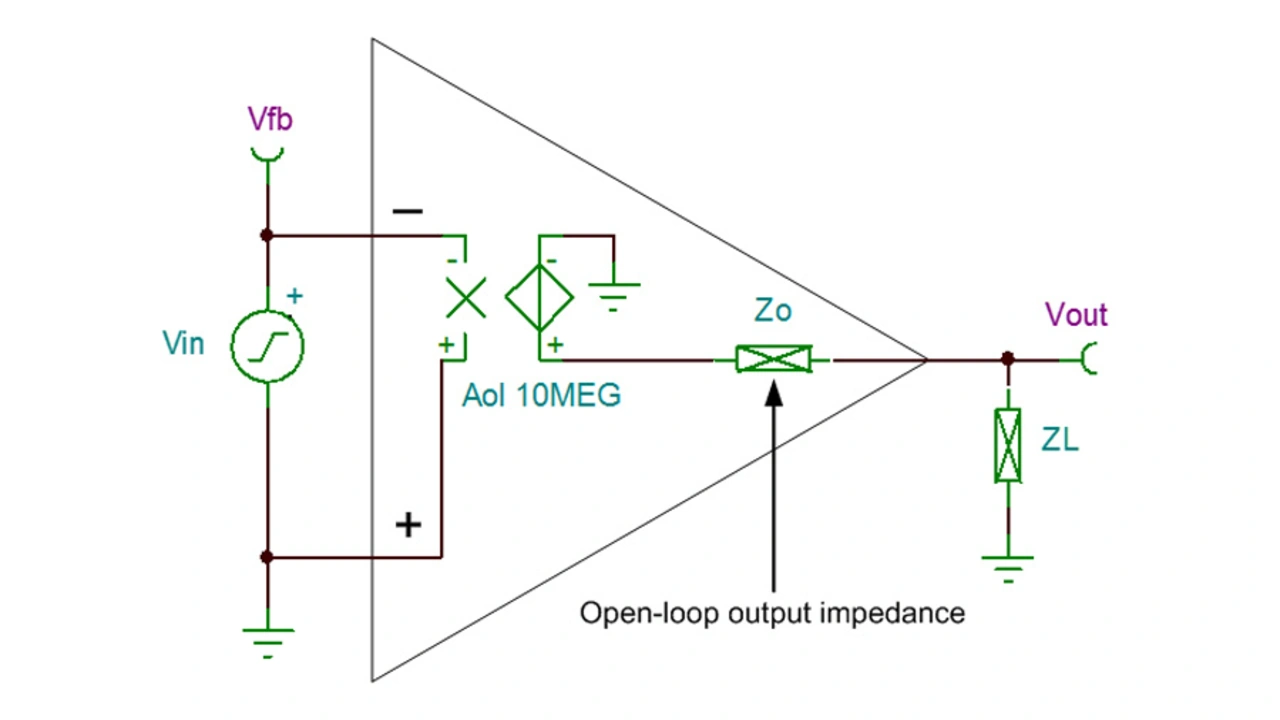
Die kritischste Spezifikation, die vor einer Stabilitätsanalyse auf Genauigkeit zu prüfen ist, ist die Leerlauf-Ausgangsimpedanz (ZA0) des Operationsverstärkers.
Man kann sich ZA0 ganz einfach als komplexe Impedanz im Kleinsignalpfad des Operationsverstärkers vorstellen, die sich zwischen der Verstärkerstufe und dem Ausgangsanschluss befindet.
Diese Impedanz interagiert sowohl mit der Verstärkerstufe des Operationsverstärkers als auch mit der Last und der Rückkopplung. Zusammen entscheiden diese Komponenten über das dynamische Verhalten der Schaltung. Bild 24 zeigt in vereinfachter Form ZA0 in einer Operationsverstärkerschaltung ohne Rückkopplung.
Wenn ein Operationsverstärker-Hersteller die Leerlauf-Ausgangsimpedanz ZA0 nicht korrekt modelliert, ist das gesamte dynamische Kleinsignal-Verhalten des Operationsverstärkermodells falsch, sodass es nicht für Stabilitätsanalysen herangezogen werden kann.
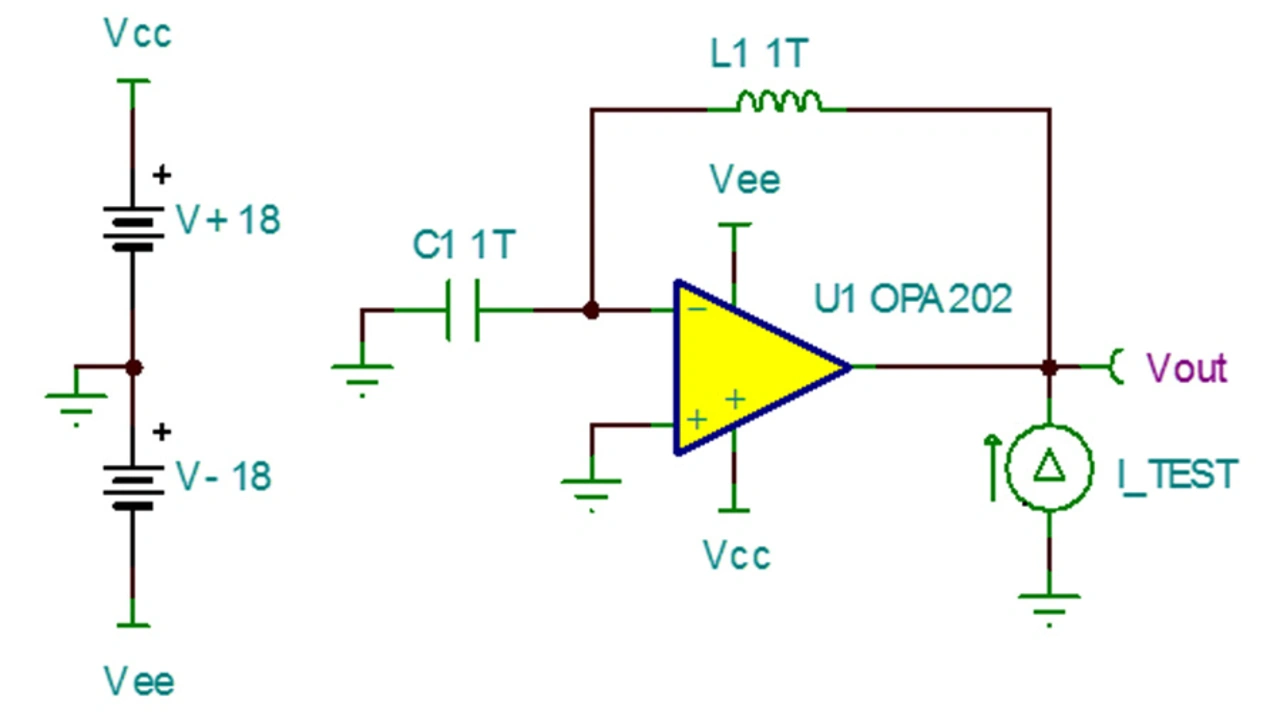
Glücklicherweise lässt sich einfach verifizieren, ob der ZA0-Wert eines Modells der Datenblattangabe entspricht. Die empfohlene Schaltung hierfür ist in Bild 25 dargestellt.
In dieser Prüfschaltung schließt die Induktivität L1 bei DC die Rückkoppelschleife, wogegen bei AC eine Analyse im Leerlauf möglich ist. Der Kondensator C1 verbindet den invertierenden Eingang bei AC mit der Masse, damit dieser nicht potenzialfrei ist.
Die AC-Stromquelle ITest steuert den Operationsverstärkerausgang an, und durch Messen der resultierenden Spannung am Ausgang lässt sich nach dem ohmschen Gesetz die Ausgangsimpedanz berechnen.
Um ZA0 grafisch aufzuzeichnen, wird eine AC-Übertragungsfunktion über den gewünschten Frequenzbereich durchlaufen und die Ausgangsspannung UA aufgezeichnet. Nicht besonders viele Simulatoren geben die Ergebnisse standardmäßig in Dezibel aus. Wird das Messergebnis mit logarithmischem Maßstab aufgetragen, entspricht UA der Angabe in Ω.
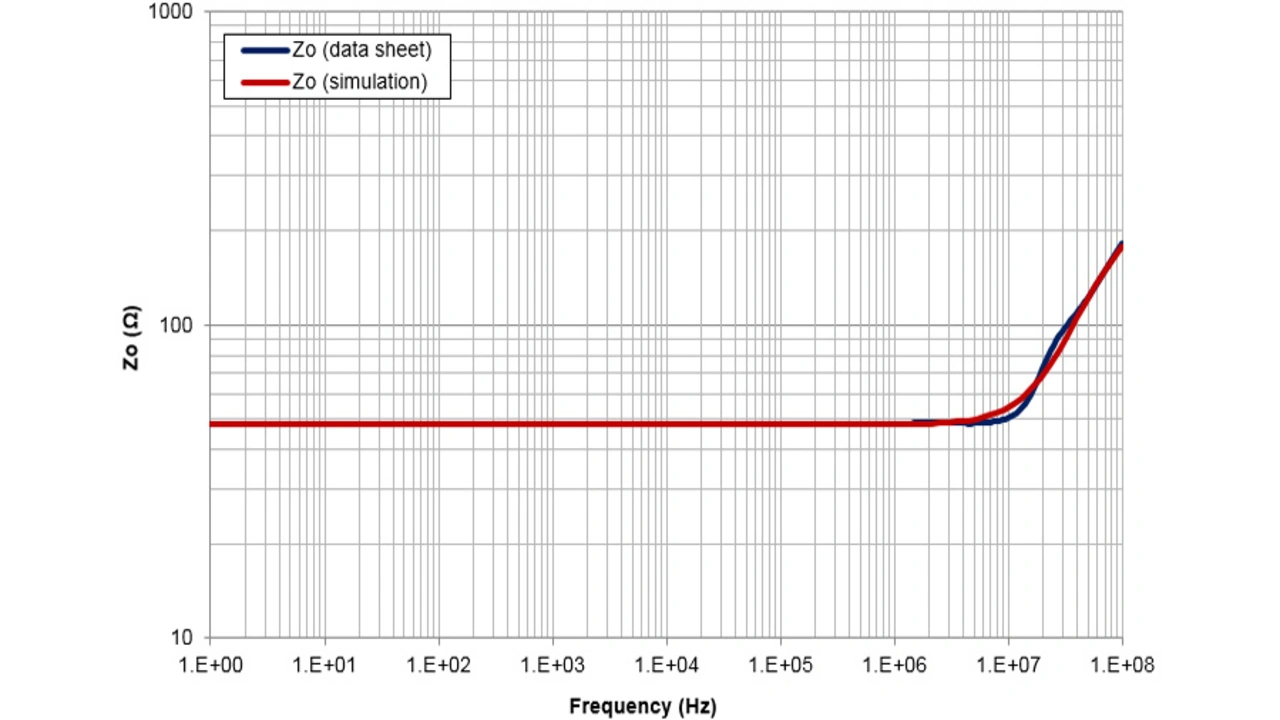
Nachfolgend wird der ZA0-Wert des OPA202 [23], eines neuen Präzisions-Bipolarverstärkers von Texas Instruments, getestet.
Der modellierte ZA-Wert des Operationsverstärkers entspricht im vorliegenden Fall ziemlich gut der Angabe im Datenblatt überein (Bild 26). Bis etwa 1 MHz hat die Ausgangsimpedanz einen sehr flachen (resistiven) Verlauf, wie es für klassische Operationsverstärker üblich ist.
Mit der Erkenntnis, dass der ZA-Wert des Modells korrekt ist, kann es nun an die Prüfung des übrigen Kleinsignalverhaltens gehen.
Kleinsignal-Überschwinger
Eine der einfachsten Möglichkeiten, die Stabilität eines Operationsverstärkers zu überprüfen – ob in der Simulation oder in der Realität –, besteht darin, das prozentuale Überschwingen am Ausgang als Reaktion auf eine sprunghafte Änderung des Eingangssignals oder ein Rechtecksignal am Eingang zu messen.
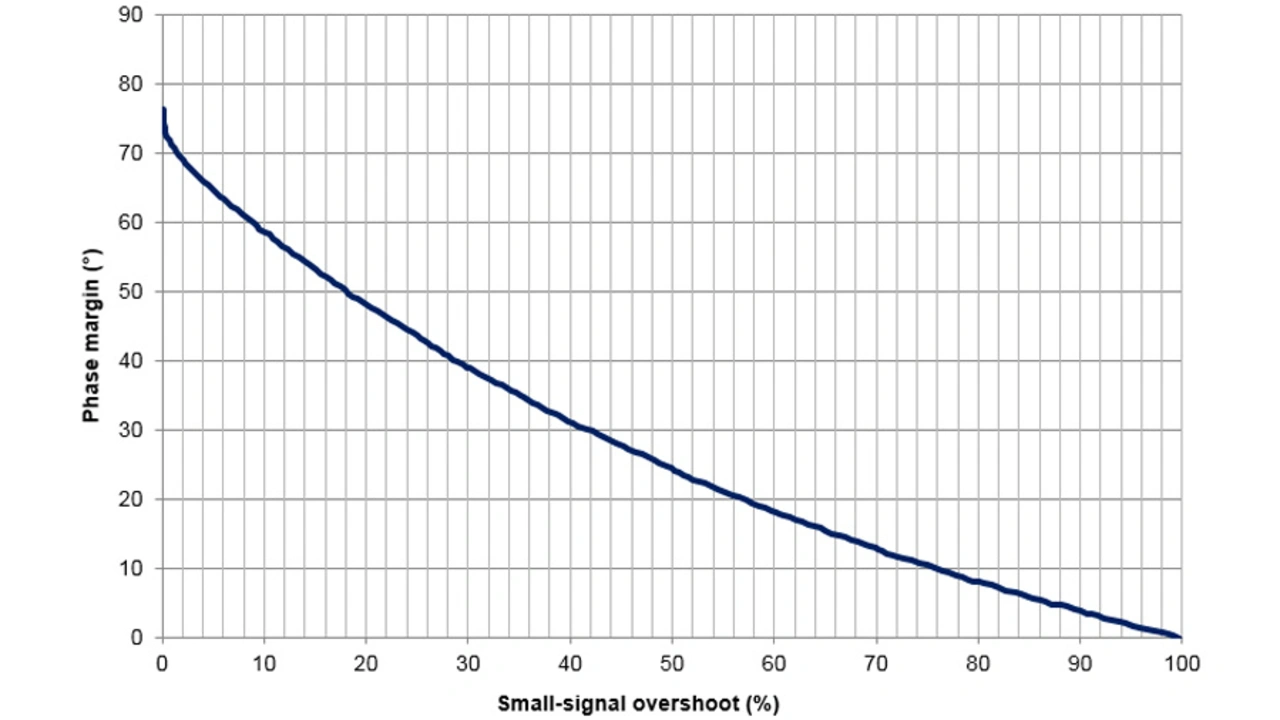
Unter der Annahme, dass die Operationsverstärkerschaltung ein System zweiter Ordnung ist, kann das Überschwingen mit der Phasenreserve – und folglich mit der Stabilität – in Zusammenhang gebracht werden, wegen der mathematischen Beziehung zwischen beiden über den Dämpfungsfaktor.
Bild 27 verdeutlicht diese Beziehung anhand eines von 0 bis 100 % zunehmenden Überschwingens. Kleinsignal-Überschwinger lassen sich sowohl in invertierenden als auch in nicht-invertierenden Verstärkerschaltungen prüfen.
Als Beispiel für die weitere Untersuchung dient ein invertierender Verstärker (Bild 28).
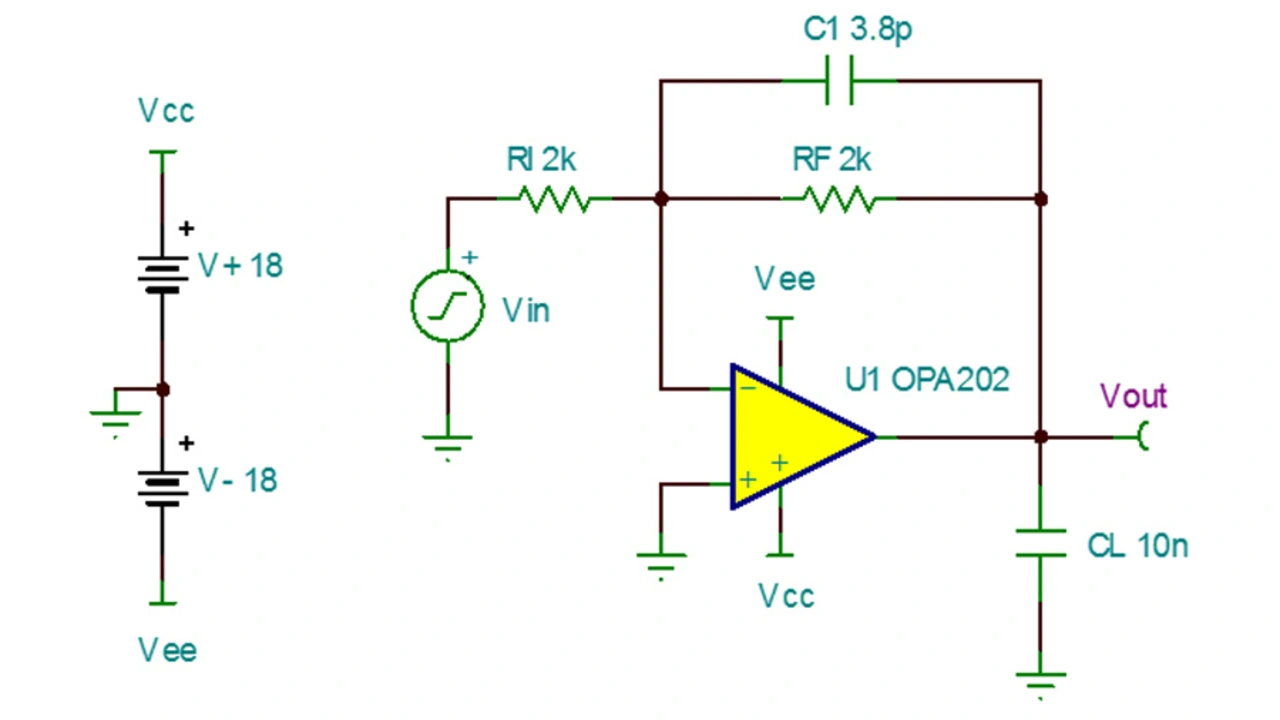
RF und RI wurden, entsprechend des typischen Lastwiderstands des Operationsverstärkers, mit 2 kΩ dimensioniert. Sie sorgen für eine Schleifenverstärkung von –1 V/V. C1 dient der Kompensation der Eingangskapazität des Operationsverstärkers und wird mit einem Kapazitätswert entsprechend der Summe aus CGl + CDiff gewählt.
Als Lastkapazität CL wird ein Wert von 10 nF angenommen. Am Eingang wird für UE ein Rechtecksignal mit 5 mVSS und 10 kHz genutzt, um sicherzustellen, dass nur das Kleinsignalverhalten des Operationsverstärkers zum Tragen kommt.
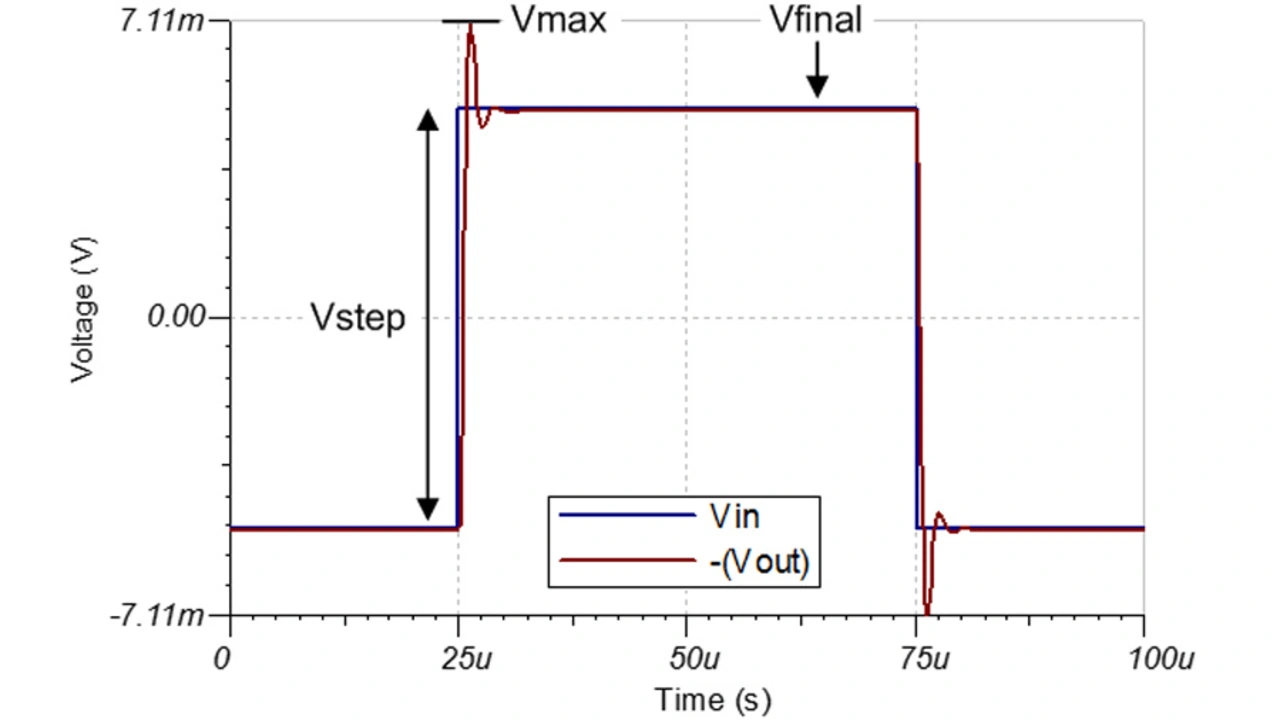
Mit dieser Schaltung werden jetzt die Kleinsignal-Überschwinger des OPA202 gemessen. Hierzu wird zunächst eine Transientenanalyse über eine Periode (100 µs) durchgeführt, um die Spannungen am Eingang (UE) und am Ausgang –UA grafisch aufzuzeichnen.
Da hier die Grundschaltung eines invertierenden Verstärkers gewählt wurde, empfiehlt es sich das Ausgangssignal zu invertieren, um es leichter mit dem Eingangssignal vergleichen zu können.
Die Gleichungen 1 und 2 dienen zum Berechnen des prozentualen Überschwingens:
Darin steht UA max für die maximale Ausgangsspannung, UA final ist die finale Ausgangsspannung nach erfolgtem Einschwingvorgang und UA gesamt ist die Gesamt-Sprungamplitude am Ausgang.
Aus Bild 29 lässt sich ablesen, dass ein Überschwingen von 21,1 % einer Phasenreserve von etwa 47 ° entspricht.
Eine allgemeine Stabilitätsempfehlung lautet, dass eine Verstärkerschaltung eine Phasenreserve von mindestens 45 ° haben sollte. Diese Vorgabe ist hier also gerade eben erfüllt.
Durchaus bemerkenswert ist die Tatsache, dass der OPA202 auch an einer Lastkapazität von 10 nF noch stabil arbeitet.
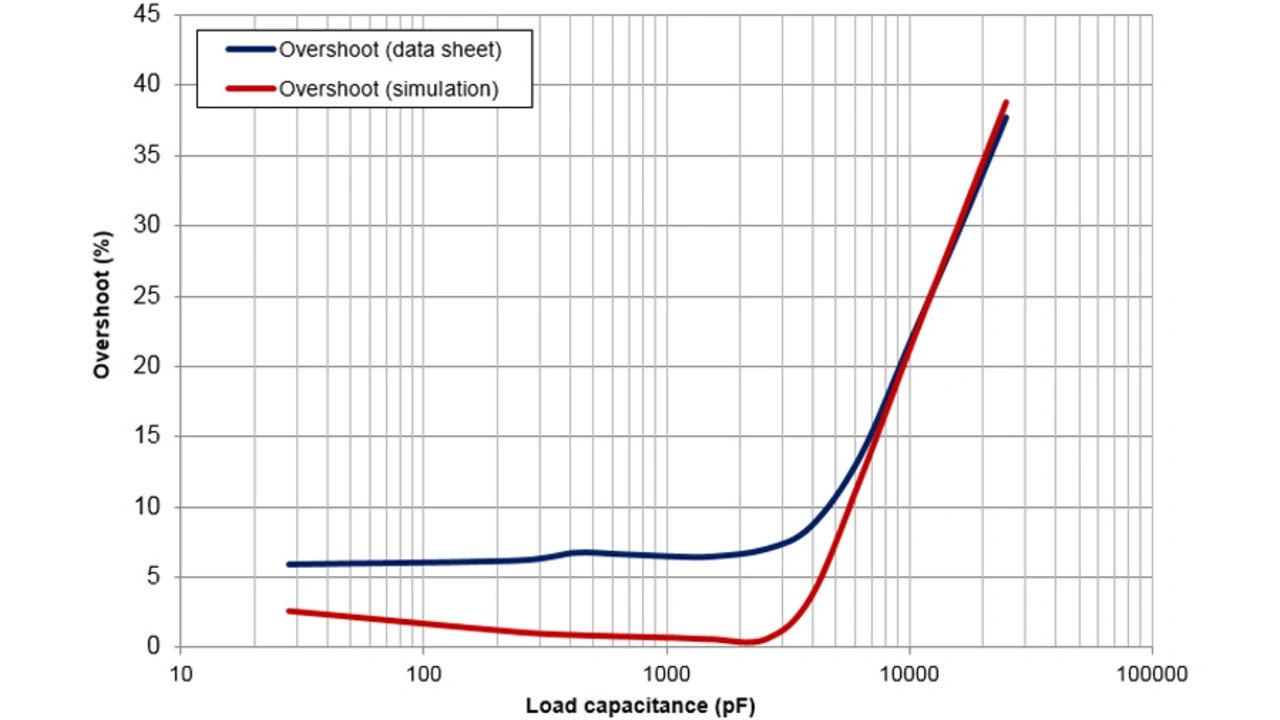
Dieser Test kann mit unterschiedlichen Lastkapazitäten wiederholt werden, um festzustellen, wie gut ein Modell mit den Lastkapazitäts-Spezifikationen im Datenblatt übereinstimmt (Bild 30).
Im Bereich von etwa 30 pF bis 25 nF, deckt sich das Überschwingen des SPICE-Modells des OPA202 gut mit der Kurve aus dem Datenblatt – besonders bei höheren Lastkapazitäten. Dies lässt darauf schließen, dass die Kleinsignal-Eigenschaften des SPICE-Modells sehr gut denen des realen ICs entsprechen und dass jegliche in der Simulation vorgenommene Stabilitäts-Kompensation auch in der realen Schaltung funktioniert.
Literatur
[22] Wells, C.: Op Amps: Stability 1. Texas Instruments, TI Precision Labs, März 2015, https://training.ti.com/ti-precision-labs-op-amps-stability-1?cu=14685.
[23] OPA202 Precision, Low-Noise, Heavy Capacitive Drive, 36-V Operational Amplifier, Texas Instruments, Datenblatt, September 2018, www.ti.com/lit/ds/symlink/opa202.pdf.
[24] Kay, A.; Green, T.: Analog Engineer’s Pocket Reference. Texas Instruments, 4. Auflage, April 2015, www.ti.com/general/docs/litabsmultiplefilelist.tsp?literatureNumber=slyw038b.
[25] Trump, B.: SPICEing Op Amp Stability. Texas Instruments, TI E2E Community, 10. September 2012, www.ti.com/lit/slyw038.
[26] Wells, C.; Oljaca, M.: Modeling the output impedance of an op amp for stability analysis. Texas Instruments, Analog Applications Journal, 2016, 3Q, www.ti.com/lit/an/slyt677/slyt677.pdf.
[27] Mancini, R.: Op amp stability and input capacitance. Texas Instruments, Analog Applications Journal, 2004, 1Q, www.ti.com/lit/an/slyt087/slyt087.pdf.
Der Autor

Ian Williams, B. Sc.
ist Applikationsingenieur und SPICE-Modellentwickler für Präzisionsverstärker bei Texas Instruments in Tucson, Arizona, USA. Er erhielt seinen Bachelor in Elektrotechnik von der Universität von Texas in Dallas.
asktexas@ti.com