Startseite > Automotive > Assistenzsysteme > Bausteine für die neuen ADAS

Radarsignale erfassen und bearbeiten

Bausteine für die neuen ADAS

4. September 2015, 13:35 Uhr | Von Peter Aberl

▶ Diesen Artikel anhören

Fortsetzung des Artikels von Teil 1

Signalerfassung und -verarbeitung

Für die Analyse der Differenzfrequenz sind ein leistungsfähiger A/D-Wandler (ADC) und ein digitaler Signalprozessor (DSP) erforderlich. Bevor der ADC das Eingangssignal abtastet und das herabgemischte analoge Basisbandsignal digitalisiert, muss das Signal ein Anti-Aliasing-Filter und einen rauscharmen Verstärker durchlaufen. Sinnvoll wäre auch ein Equalizer zur Kompensation entfernungsabhängiger Signalverluste. Die Erfassung und Analyse des digitalisierten Signals übernimmt der DSP, der die Entfernungs-, Geschwindigkeits- und Winkelinformationen aus den Daten extrahiert. Dies geschieht mit den in Bild 2 skizzierten Schritten.

Jobangebote+ passend zum Thema

Regional Key Account (m/w/d) für Elektronische Bauteile

KOA Europe GmbH, Dägeling

Alle Jobangebote im Elektroniknet Karrierebereich anzeigen

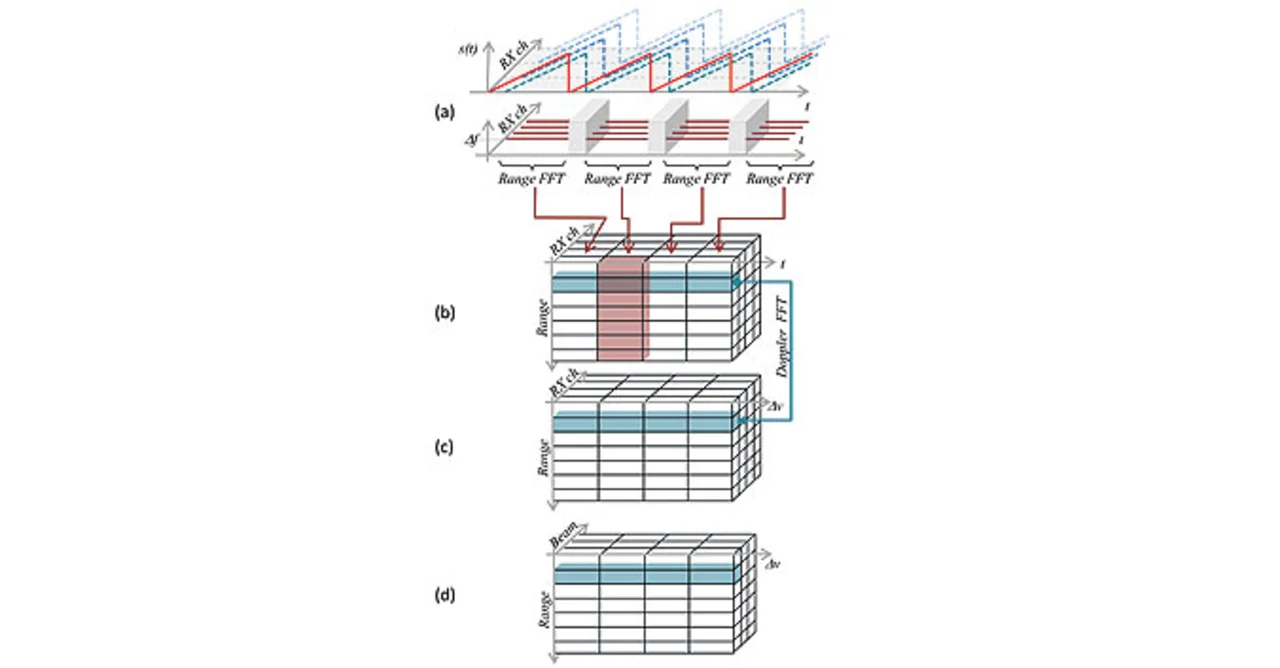
Die Verarbeitung des Radarsignals erfolgt mit zwei orthogonalen FFTs sowie durch digitales Beamforming und einen Zieldetektor. Die erste FFT-Stufe ermittelt die Entfernung der Objekte, die eine Signalreflexion verursacht haben. Diese wird als „Range FFT“ bzw. „Entfernungs-FFT“ bezeichnet (Bild 2b). Wie bereits erwähnt, ist die Frequenzverschiebung direkt proportional zur Signallaufzeit und damit zur Distanz, in der sich das Objekt befindet. Wenn die Range FFTs aller Chirps und aller Empfangskanäle berechnet sind, lässt sich die relative Geschwindigkeit Δv der Objekte ermitteln, indem man die Ergebnisse der Range-FFT-Funktion mit der orthogonalen Doppler-FFT-Funktion verarbeitet. Dies geschieht, indem man gleiche Entfernungsresultate aller Range-FFTs aus einem Empfangskanal als Eingangsdaten für die Doppler-FFT-Funktion verwendet (dargestellt als horizontale blauen Balken in Bild 2b und 2c).

Dank der Verwendung des Fast-Chirp-Verfahrens sind die Bins gleicher Entfernung jeweils um eine Chirp-Periode voneinander entfernt. Die relative Geschwindigkeit der Objekte führt zu einer Phasenverschiebung zwischen dem Range Bin, einem Häufigkeitszähler für einen bestimmten Entfernungsbereich, von Chirp (n) und dem Range Bin von Chirp (n+1), die ein Maß für die Doppler-Frequenz ist. Dieser Vorgang wird für alle Range Bins und alle Empfangskanäle wiederholt. Als Resultat nach der Range-FFT- und der Doppler-FFT-Funktion steht für jeden Empfangskanal eine zweidimensionale Range-Doppler-Matrix zur Verfügung, bei deren Elementen es sich um komplexe Werte mit einem Real- und einem Imaginärteil handelt.

In einem dritten Schritt lässt sich der Azimutwinkel der Objekte ermitteln. Hierzu erfolgt ein digitales Beamforming (DBF) der Range-Doppler-Matrizen für die verschiedenen Empfangskanäle. Eine ebenso einfache wie effiziente Art des digitalen Beamforming besteht darin, die Elemente der Range-Doppler-Matrix mit einer vorgegebenen Phasenverschiebung zu versehen, um die Signallaufzeiten n · τ (Bild 3) zu kompensieren.

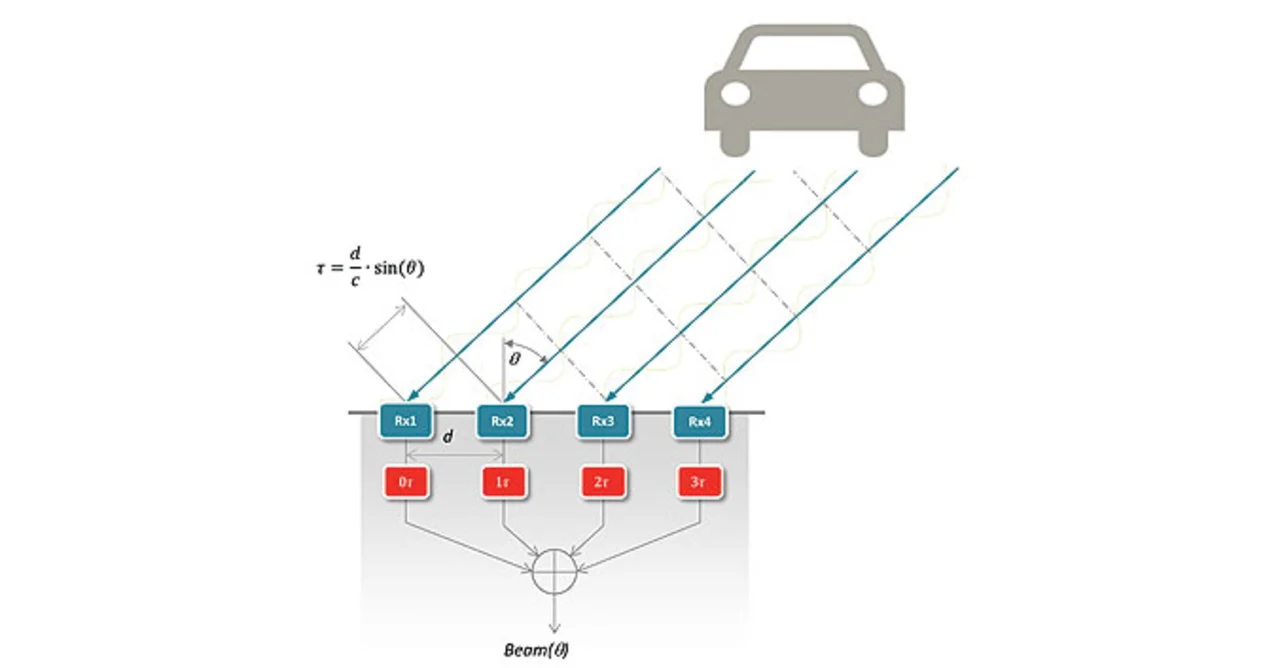
Die Phasenverschiebungswerte sind von den Eigenschaften und Abmessungen der physischen Antennenflächen, vom Empfangskanal und vom Zielwinkel abhängig. Dieses auch als „statisches DBF“ bezeichnete Verfahren lässt sich einfach umsetzen, indem man komplexe Multiplikationen der einzelnen Elemente der Range-Doppler-Matrix mit den zuvor bestimmten Phasenverschiebungen ausführt, gefolgt von einer Summierung über alle Empfangskanäle hinweg. Die gerade beschriebene Prozedur muss für jeden digitalen Strahl wiederholt werden. Das Resultat ist eine dreidimensionale komplexe Range-Doppler-Azimut-Matrix, wie sie in Bild 2d zu sehen ist.

Bevor es mit dem finalen Schritt zur Verarbeitung der Radarsignale weitergehen kann, muss die komplexe Matrix in eine Matrix mit Absolutwerten verwandelt werden, die absolute Leistungswerte wiedergeben. Die Elemente der Matrix werden von Störungen durch Mehrwegempfang, Hintergrundrauschen und Interferenzen aus anderen Quellen in der Nähe überlagert. Da die Störgrößen räumlich und zeitlich stark variieren können, wird ein adaptives Filter benötigt, das mit diesen wechselnden Bedingungen zurechtkommt und dabei die wahrscheinlichsten Ziele finden kann. Ein zuverlässiges Filter ist der sogenannte OS-CFAR-Detektor. OS-CFAR steht für Order Statistic Constant False Alarm Rate.

Mit dem Ziel, eine konstante Fehlalarm-Rate zu erreichen, wird die Ansprechschwelle in einem CFAR-Detektor ein Element nach dem anderen anhand der geschätzten Störleistung eingestellt. Letztere wird bestimmt, indem man eine Gruppe von Referenzelementen in der Umgebung des untersuchten Elements (Element Under Investigation, EUI) verarbeitet. Die umgebenden Elemente werden zunächst nach ihren Absolutwerten sortiert. Dann ist der Wert des sortierten Elements mit dem Rang R das Referenzelement, das mit dem EUI verglichen wird. Ist das EUI geringer als das Referenzelement, so wird das EUI auf 0 gesetzt. Im anderen Fall wird das EUI zu einem Ziel. Je höher der Rang R gesetzt wird, umso restriktiver wird das Filter bei der Detektierung von Zielen. Darüber hinaus kann ein Offsetwert zu dem Referenzelement mit dem Rang R addiert werden, um den Detektor robuster zu machen.

Der OS-CFAR-Detektor wird auf jedes Element des Entfernungs-Doppler-Azimut-Array angewendet. Ausgegeben wird eine dünn besetzte dreidimensionale Ziel-Matrix, die an einen applikationsspezifischen Tracking-Algorithmus übergeben wird. Dieser Tracker nutzt die Ziel-Matrix als Referenz zum Korrelieren der Zielinformationen mit existierenden Tracks, d.h. Objekten. Außerdem übernimmt der Tracker das Entfernen alter und das Erstellen neuer Tracks.