Sigma-Delta-Modulator
PLDs als A/D-Wandler
Fortsetzung des Artikels von Teil 1
Digitaler Tiefpassfilter
Die wesentliche Aufgabe des Digitalfilters ist, das Quantisierungsrauschen zu dämpfen, bevor die Abtastfrequenz abgesenkt wird und sich dieses Rauschen in die Nutzbandbreite hinein faltet. Da das Quantisierungsrauschen bei einem ∑Δ-Modulator erster Ordnung mit etwa 20 dB pro Dekade ab fO ansteigt, genügt für einfache Anwendungen auch ein digitaler Tiefpass erster Ordnung. Eine weitere Funktion dieses Filters ist es, die Wortbreite von einem Bit auf N Bits zu erhöhen, weshalb er oftmals auch als Konvertierungsfilter bezeichnet wird. Hierzu eignen sich verschiedene Filtertypen [6].
Ein rücksetzbarer Vorwärts-Rückwärts-Zähler mit N Bits (Bild 3) stellt einen minimalen Aufwand für einen solchen Filter dar. Dieser besitzt eine Übertragungsfunktion nahezu wie ein SINC-Filter erster Ordnung mit M = 2N-1 Stufen, da er 2N-1-1 Ausgangsbits des ∑Δ-Modulators mittelt, anstatt 2N-1 wie beim entsprechenden SINC-Filter. Durch das Rücksetzen des Zählers nach 2N-1 Abtastungen, ergibt sich eine zweite Zeitbasis, wodurch die z-Transformation nicht mehr geschlossen angewendet werden kann [7]. Das einen Takt lange Rücksetzen des Zählers hat den Vorteil, dass dieser ausgangsseitig maximal den Wert +(2N-1-1) und minimal den Wert –(2N-1-1) annehmen kann. Dadurch ist die Wortlänge des Zählers sehr gut ausgeschöpft und der zu vermeidende Zweierkomplementüberlauf sicher unterbunden.
Für N = 8 Bit ist daher ein Filter mit 26 Makrozellen des verwendeten PLDs zu realisieren. Der SINC-Filter erster Ordnung mit Differenzierer und Integrierer konnte dagegen mit allen zur Verfügung stehenden 144 Makrozellen nur für M = 112 erstellt werden. Durch Vertauschen der Reihenfolge auf Integrierer und Differenzierer ließ sich dieser Filter mit 50 Makrozellen aufbauen. Ein leckender Akkumulator mit k = 0,99609375 (m = 8) und 8 Bit Ausgangswortbreite war mit 61 Makrozellen zu realisieren.
Testaufbau
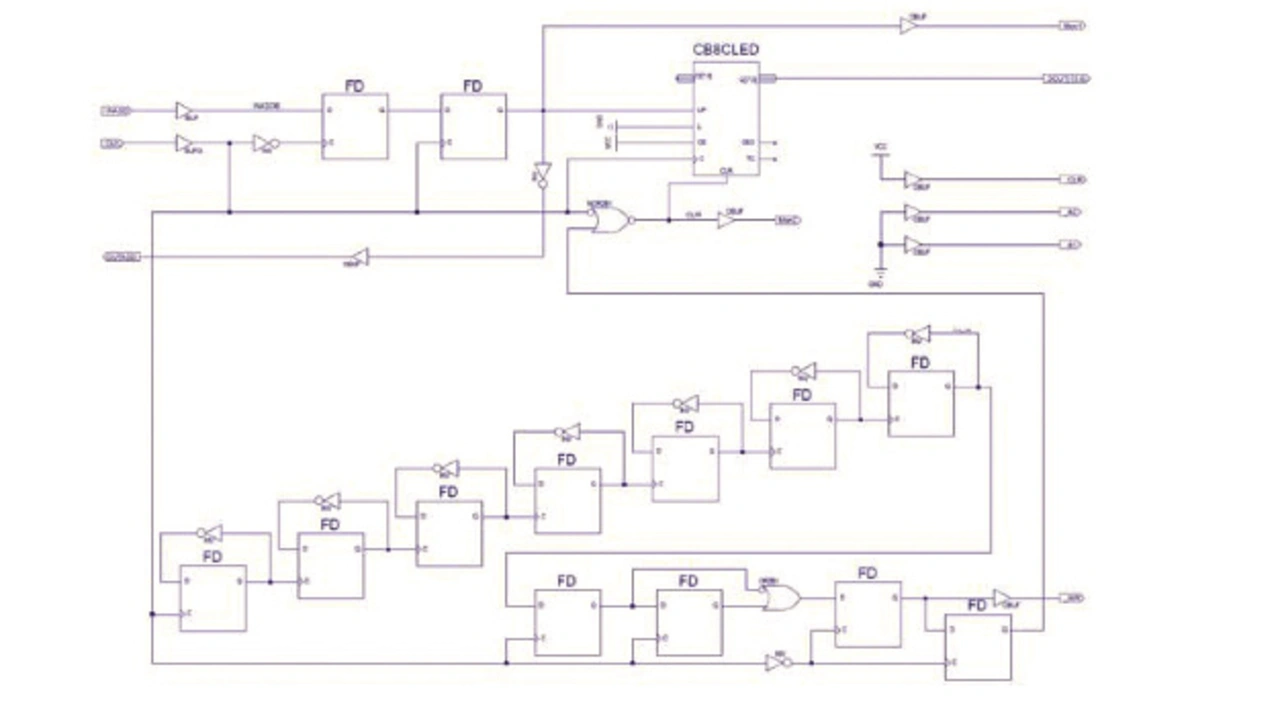
In Bild 3 ist das Blockschaltbild zum Testaufbau des ∑Δ-ADC zu sehen. Der ∑Δ-Modulator besteht hier aus zwei D-Flipflops, die mit verschiedenen Flanken der Abtastfrequenz fS von 12 MHz getriggert werden, um metastabile Zustände zu unterdrücken. Die aus Kombination R1, R2 und C1 des Modulators wurde zu mit einer oberen Grenzfrequenz fO von 14,4 kHz gewählt. Der Ausgang des ∑Δ-Modulators ist auf den Kontrollanschluss Mon1 geführt. Um zu zeigen, dass in der Ausgangspulsfolge des Modulators tatsächlich auch das analoge Eingangssignal enthalten ist, wird hier ein analoger Tiefpass zweiter Ordnung mit einer Eckfrequenz fg von 15,4 kHz angeschlossen. An dessen Kontrollausgang ANA kann das Analogsignal nachvollzogen werden. Mit der PLD-Versorgungsspannung UCC von 3,3 V kann der Spitze-Spitze-Wert der analogen Eingangsspannung maximal in etwa diesen Wert annehmen.
Der Ausgang des ∑Δ-Modulators wird auf den UP/DOWN-Eingang eines 8 Bit breiten Vorwärts-Rückwärts-Zählers geführt. Ein High auf dieser Signalleitung wird somit als +1, ein Low als –1 interpretiert. Der Ausgang des ∑Δ-ADCs Q(7:0) besitzt somit eine Zweierkomplementdarstellung. Der hier als digitales Tiefpassfilter fungierende Zähler wird alle 128 Abtasttakte zunächst ausgelesen und dann einen Takt lang zurückgesetzt. Dadurch kann der Zählerausgang maximal den Wert +127(dez) und minimal den Wert –127(dez) annehmen, was den 8-Bit-Wertebereich sehr gut ausschöpft und den Zweierkomplementüberlauf verhindert. Wird der Teiler immer ein Bit kleiner gewählt als der Vorwärts-Rückwärts-Zähler, so ergibt sich ein symmetrisches Ausgangssignal, das nicht überlaufen kann. Bei einem Zweierkomplementüber- oder -unterlauf springt das Signal bekanntlich vom Maximal- zum Minimalwert oder umgekehrt, was sehr unangenehme Oberwellen erzeugt.
Jobangebote+ passend zum Thema
Der Ausgang des ∑Δ-ADCs Q(7:0) wird an den High-Byte-Eingang eines 16 Bit breiten Zweierkomplement-D-A-Wandlers angeschlossen. Der Low-Byte-Eingang bleibt hier unbenutzt, ist aber zum PLD hin verdrahtet, um für größere Wortbreiten am ∑Δ-ADC vorbereitet zu sein. Die symmetrische Versorgungsspannung des D-A-Wandlers von +12 V und –12 V bedingt, dass der analoge Ausgang maximal fast +10 V und minimal –10 V werden kann [8]. Die maximale Wandlungsrate des D-A-Wandlers von 100 kHz ist mit 12 MHz/128 = 93,75 kHz nahezu ausgeschöpft.
Den Zähler in Bild 3 als reinen 8-Bit-Vorwärtszähler zu gestalten und den Ausgang des ∑Δ-Modulators als dessen Enable-Eingang zu benutzen ergibt anstatt einer Zweierkomplementdarstellung eine Binary-Offset-Wertigkeit. Allerdings muss dann der zugehörige Teiler auf 2N eingestellt sein [9].
In Bild 5 ist zu sehen, wie der ∑Δ-ADC im Inneren des PLDs aufgebaut ist. Auf Basis des programmierbaren Bausteins XC95144 von Xilinx wurden hierzu nur 26 der insgesamt 144 Makrozellen benötigt. Dies stellt zusammen mit den beiden externen Widerständen R1 und R2 sowie dem externen Kondensator C1 den kompletten 8-Bit-∑Δ-ADC dar. Zu beachten ist allerdings, dass die Ausgangsdaten nur zum Zeitpunkt der positiven WR-Flanke gültig sind. Ist das nicht akzeptabel, ist ein 8 Bit breites D-Register, das mit dieser Flanke getriggert wird, nachzuschalten. Bild 6 zeigt den Testaufbau für die folgenden Messungen im Zeitbereich.
In Bild 7 sind die Signale am Eingang und an den Ausgängen des ∑Δ-ADCs bei einer Signalfrequenz von 1 kHz zu sehen. Das analoge Eingangssignal (Ch1, gelb) befindet sich mit einer Amplitude von 2,8 V nahe der Vollaussteuerung. Im Digital-Ausgang des ∑Δ-Modulators (Ch2, cyan) kann man sehen, wie die Pulsdichte entsprechend der analogen Eingangsspannung variiert. Bei niedriger Eingangsspannung tendiert dieser Ausgang zu Low- und bei hoher Spannung zu High-Impulsen. Das Ausgangssignal ANA (Ch3, magenta) zeigt, dass das Eingangssignal ziemlich exakt unter anderem auch im digital Ausgang des ∑Δ-Modulators enthalten ist. Eine minimale Schwächung der Amplitude ist wohl auf den passiven RC-Tiefpass zweiten Grades zurückzuführen. Das analoge Ausgangssignal (Ch4, grün) zeigt mit einer symmetrischen Amplituden von circa ±8,4 V, dass auch hier nahezu Vollaussteuerung vorliegt und dass das digitale Eingangssignal Q(7:0) eine Zweierkomplementwertigkeit besitzt.
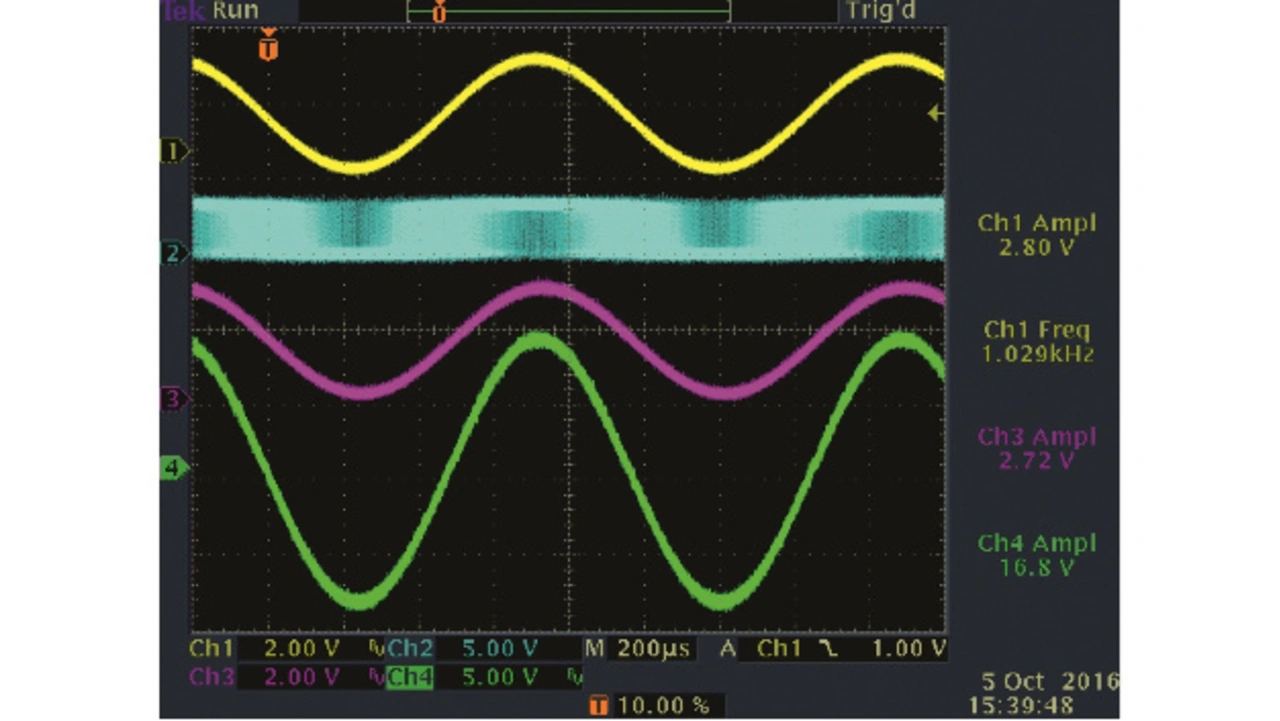
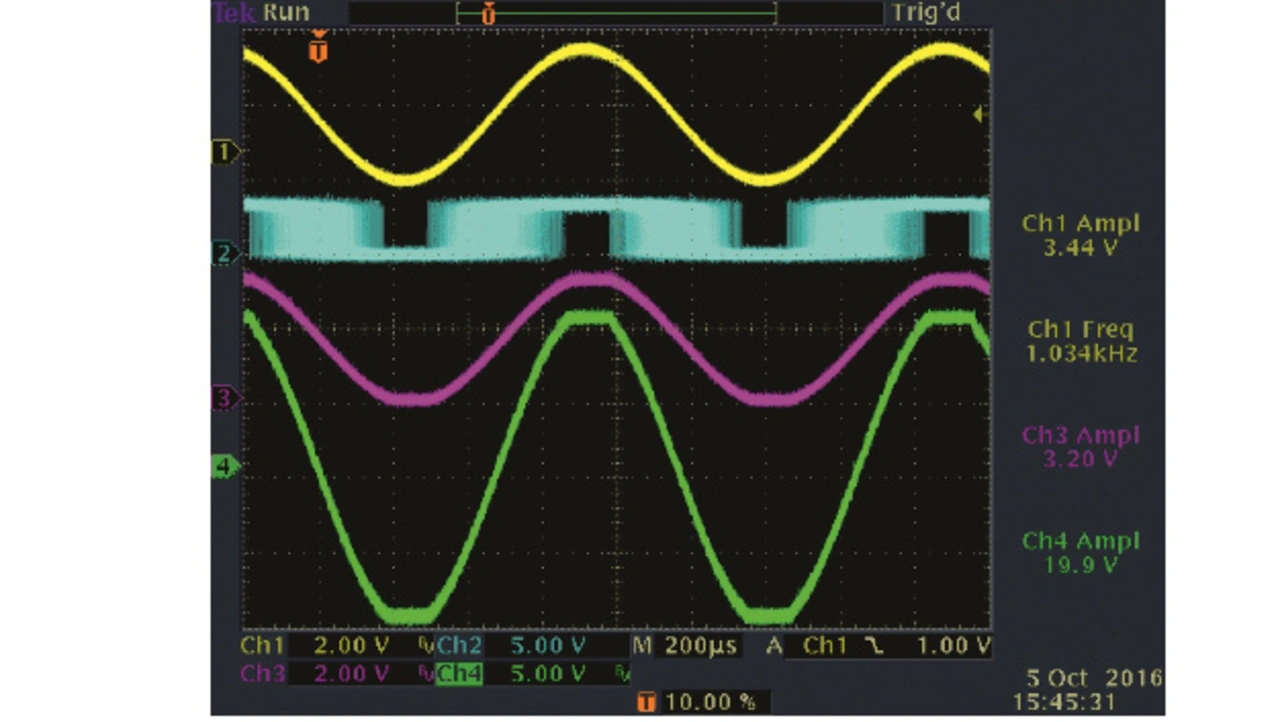
Bild 8 zeigt, wie sich dieser ∑Δ-A/D-Wandler bei Übersteuerung verhält. Eine Übersteuerung ist vor allem daran zu erkennen, dass der Ausgang des ∑Δ-Modulators (Mon1) eine Zeit lang nur noch High oder Low ausgibt.
Hierbei ist es vor allem wichtig, dass auch der analoge Ausgang auf seinem Maximalwert beziehungsweise Minimalwert stehen bleibt und eben nicht einen Zweierkomplementüberlauf zeigt. Ein exakt begrenztes Ausgangssignal bedeutet jedenfalls, dass die Wortlängen im digitalen Filter passen.
- PLDs als A/D-Wandler
- Digitaler Tiefpassfilter
- Frequenzgang
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Analoge Signalverarbeitung im μC
MSP430 mit programmierbaren Analogschaltungen
Signale von Differenzialtransformatoren
Rauscharmer digitaler AM-Demodulator
Interview mit Analog-Guru Bob Dobkin
»Wir haben von Digital sehr profitiert«
