Diagnose auf realer Zielhardware
Neuronale Netze entwickeln und testen
In Embedded-Anwendungen kommen immer häufiger neuronale Netze zum Einsatz. Wichtig ist, zu prüfen, ob das trainierte Netz auf der realen Hardware seine Aufgaben erfüllt. Aus dem Grund wurde an der TU Dresden ein Diagnosekonzept für KI-basierte Systeme auf Basis des Debuggers UDE von PLS entwickelt.
In immer mehr Bereichen der Technik greifen Entwickler auf Methoden aus dem Bereich der künstlichen Intelligenz (KI) zurück. Zu den prominentesten Anwendungen zählen dabei neuronale Netze. Sie bestehen aus zahlreichen Neuronen, die in Input, Output und Hidden Layern angeordnet sind. In Bild 1 ist ein neuronales Netz, bestehend aus einem Input und Output Layer sowie zwei Hidden Layern, dargestellt. In jedem Neuron werden einzelne (skalare) Werte a gespeichert.
Jobangebote+ passend zum Thema

Für jede Verbindung wird der Wert des Eingangsneurons ain mit einem trainierbaren Gewichtsparameter w multipliziert und danach ein ebenfalls trainierbarer Biasparameter b hinzuaddiert. Abschließend wird das Resultat über eine feste und vorab definierte Funktion g aktiviert. So entsteht die Formel:
Convolutional Neural Networks
Eine besondere Unterart von neuronalen Netzen sind die faltungsbasierten neuronalen Netze (CNN, Convolutional Neural Networks). Bei ihnen sind die Verbindungen zwischen zwei Layern über Faltungsoperationen mit Faltungsmatrizen W und anschließender elementweiser Addition mit einem Biasvektor B realisiert.
Das »Leben« eines neuronalen Netzes besteht im Allgemeinen aus den folgenden drei Phasen:
Training Phase
Mit großen Datenmengen werden alle trainierbaren Gewichts- und Biasparameter des Netzes durch Gradienten-basierte Trainingsalgorithmen angepasst. Parallel dazu wird anhand von Validationsdaten die Genauigkeit des Netzes bestimmt. Die einzelnen Elemente der Trainings- und Validationsdaten, bestehend aus Paaren von Eingangswerten sowie den zugehörigen Ausgangswerten, entsprechen den Strukturen der Input- und Output-Layer. Aufgrund der hohen Rechenintensität verwendet man für das Training von neuronalen Netzen in der Regel leistungsstarke Grafikkarten oder spezielle Cloud-Services.
Adaptation Phase
Nach der Trainingsphase können Entwickler neuronale Netze mithilfe von Optimierungsschritten wie Batchnorm Fusion oder Pruning beschleunigen. Mit geeigneten Quantisierungsverfahren werden zusätzlich die arithmetischen Operationen von Fließkomma- zu Ganzzahlformaten transformiert. Mit den Anpassungen reduziert sich die arithmetische Komplexität und ermöglicht das Ausführen von neuronalen Netzen für Embedded-Prozessoren mit akzeptabler Leistungsaufnahme und Latenz [1].
Prediction Phase
Die Prediction Phase beschreibt das Benutzen beziehungsweise Anwenden des fertig trainierten neuronalen Netzes. Typischerweise werden unbekannte Daten durch das neuronale Netz entsprechend interpretiert und ausgewertet. Ein exemplarischer Use Case ist das Erkennen von Personen in Bilddaten.
Mögliche Fehlerquellen
Gerade in sicherheitskritischen Applikationen, in denen innerhalb kurzer Zeit große Datenmengen auszuwerten und zu verarbeiten sind, bietet der Einsatz neuronaler Netze einige Vorteile. Allerdings lediglich dann, wenn es auf der realen Hardware wie gewünscht funktioniert. Zu einhundert Prozent abklären lässt sich das letztendlich nur mit einer ausführlichen Hardwarediagnose, denn leider gibt es eine ganze Reihe potenzieller Fehlerquellen. Sie lassen sich im Wesentlichen in folgende Kategorien unterteilen:
Konvertierungsfehler
Beim Konvertieren in der Adaptation Phase können fehlerhafte Quantisierungen zu arithmetischen Über- und Unterläufen führen und somit die Qualität der Prädiktionen mindern.
Portieren
Nach der Adaption können beim Portieren des quantisierten Modells Fehler wie das Überschreiten von Speicherlimitationen, fehlerhaftes Programmieren der Schnittstellen oder Ähnliches auftreten.
Fehlerhaftes Implementieren
Beim Implementieren von neuronalen Netzen existieren viele Fehlerquellen hinsichtlich Arithmetik, Ablaufsteuerung und Datenmanagement. Mit Frameworks wie dem »X-CUBE-AI« von STMicroelectronics stellen MCU-Hersteller bereits geprüften und funktionsfähigen Code bereit. Allerdings sind beim Anpassen oder Erweitern erneut ähnliche Fehlerquellen denkbar. Besonders bei sicherheitskritischen Anwendungen von neuronalen Netzen muss man sich deshalb unbedingt deren Korrektheit vergewissern.
Um künftig ein möglichst schnelles, hocheffizientes Überprüfen und Verifizieren all jener Faktoren zu ermöglichen, wurde an der TU Dresden in Zusammenarbeit mit PLS Programmierbare Logik & Systeme ein neues Diagnosekonzept für KI-basierte Systeme entwickelt. Es zielt ausschließlich auf die Verifikation der Hardware des neuronalen Netzes ab. Falsche Ergebnisse aufgrund von mangelhaftem Training, Unterdimensionierung oder unvollständiger Fallabdeckung in den Trainingsdaten sind nicht Gegenstand der Diagnose. Solche Themen sind vor dem Portieren des Netzes abzuklären.
Das Diagnosekonzept
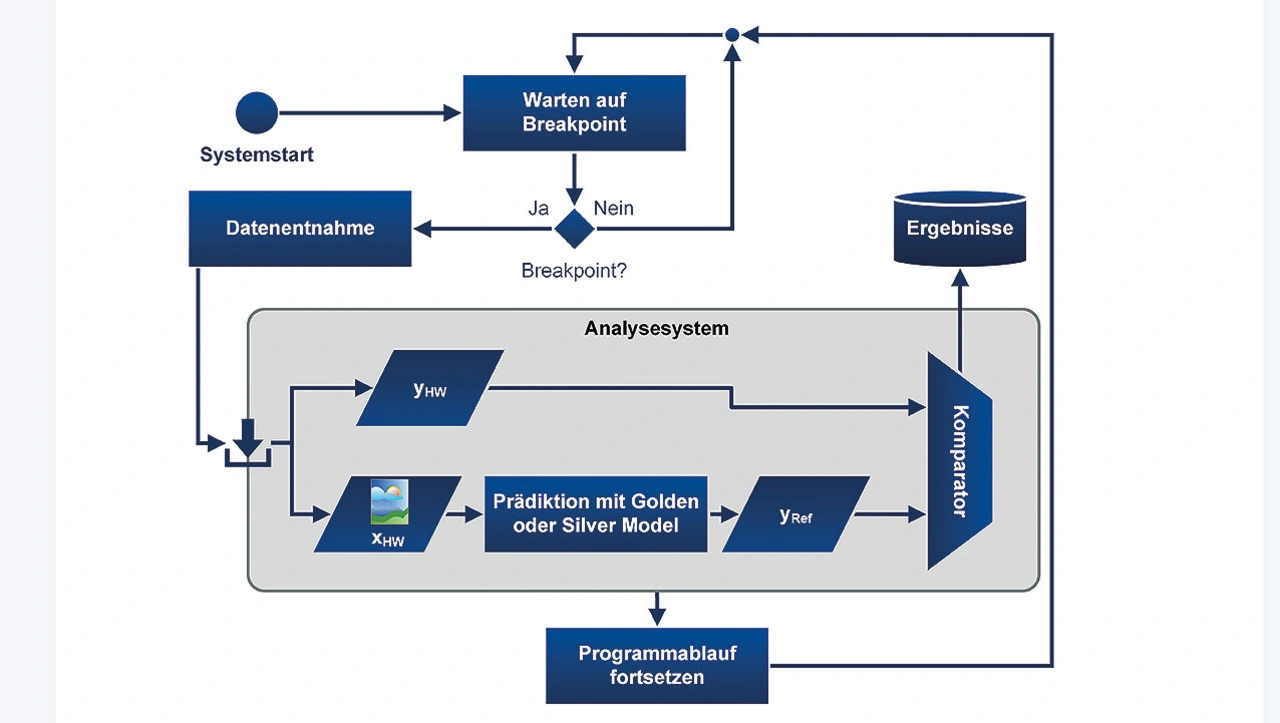
Die zentrale Komponente des Diagnosekonzeptes bildet ein neues Analysesystem, welches in Bild 2 schematisch dargestellt ist. Für die Analyse liest der Entwickler zunächst die Inputmatrix xHW und Outputmatrix yHW einer beliebigen Hardwarerealisierung eines neuronalen Netzes aus. Hierbei zeigt der Index »HW« an, dass die Matrizen von der Hardware stammen.
Je nach Anwendung variieren die Dimensionen der Matrizen. Beispielsweise kann die Inputmatrix x für Bildverarbeitung folgende Dimensionen aufweisen:
dim(x) = (1280,720,3) (Breite, Höhe, RGB-Farbtiefe). Ein neuronales Netz für Bildklassifikation ordnet der Inputmatrix x zum Beispiel die Klassen »cat« oder »dog« zu. Diese Ausgabe ist typischerweise durch eine zweielementige Outputmatrix y mit dim(y) = (2,1) zu codieren, bei der die Elemente der Klassenwahrscheinlichkeit für cat oder dog entsprechen.
Das Validieren der Outputmatrix yHW erfolgt über den Vergleich mit einem Referenzmodell, das mit dem gleichen Input xhw gefüttert wird und die Outputmatrix yRef liefert. Je nach Verfügbarkeit zieht man als Referenzmodell entweder ein Golden oder Silver Model heran.
Das Golden Model ist das Resultat des Trainings eines neuronalen Netzes und liegt als Model-Datei vor. Sie enthält Struktur, trainierte Parameter und weitere Metainformationen. Für die »Prediction«, also die spätere Anwendung des Netzes auf unbekannte Daten, wird in der Regel Fließkommaarithmetik verwendet. Das Silver Model entsteht über die sogenannte Adaptation aus dem Golden Model. Hierbei umfasst die Adaptation Optimierungs- und Quantisierungsschritte und überführt zudem die Fließkommaarithmetik in Ganzzahlarithmetik mit deutlich geringer Komplexität [2].
Im Allgemeinen treten aufgrund der Anpassungsschritte Optimierungs- und Quantisierungsverluste auf, die jedoch lediglich zu geringen Abweichungen zwischen yref von Golden und Silver Model führen. Trotzdem empfiehlt es sich, durch weitere Tests mit den Validationsdaten sicherzustellen, dass die Abweichungen in einem akzeptablen Rahmen liegen. Nach dem erfolgreichen Generieren des Silver Models ist es auf das Target Device portierbar. Sofern die Hardwareumsetzung des neuronalen Netzes korrekt implementiert ist, gelten folgende Zusammenhänge zwischen den Output-Matrizen:
Ersterer lässt sich über eine binäre Äquivalenzprüfung für yHW und yRef,Silver prüfen. Bei exaktem Übereinstimmen liefert diese »TRUE«, ansonsten »FALSE« zurück. Für den zweiten Zusammenhang werden die zu erwartenden Abweichungen durch eine Differenzmetrik, zum Beispiel dem mittleren quadratischen Fehler (Mean Squared Error, MSE), quantifiziert. Die jeweilige Prüfung, hier als Analysesystem bezeichnet, ist in eine Diagnoseschleife eingebettet, in der nach dem Systemstart fortlaufend an geeigneten Breakpoints die Input- und Outputmatrizen xHW, yHW der Hardware ausgelesen werden (Bild 2).
Nicht trivial ist das Festlegen der Breakpoints. So ist unbedingt zu gewährleisten, dass die ausgelesenen Input- und Outputmatrizen zusammengehören. In der Regel ist hier manuell und für jede Anwendung individuell vorzugehen.
Das Realisieren der Diagnoseumgebung auf dem Host-PC erfolgte als Python-Script. Für das Auslesen der Input- und Output-Matrizen xHW, y HW und die Ablaufsteuerung der Zielhardware greift das Script auf die Automatisierungsschnittstelle des Debuggers UDE (Universal Debug Engine) von PLS Programmierbare Logik und Systeme zurück. Alle nötigen Schritte der Diagnose wie Systemstart, Ablaufsteuerung und Datenentnahme sind somit besonders effizient realisierbar. Der Debugger UDE unterstützt nicht nur viele High-End-Microcontroller und Multicore-SoCs, die sich gut für KI-Anwendungen eignen. Mit den Zugangsgeräten der Universal-Access-Device-Familie gewährleistet sie auch eine schnelle und sichere Kommunikation mit dem jeweiligen Target-System.
- Neuronale Netze entwickeln und testen
- Der Praxistest