Impedanzspektren
Wenn ein Kondensator zur Spule wird
Kondensatoren verhalten sich kapazitiv – allerdings nur unter bestimmten Betriebsbedingungen und abhängig vom Frequenzbereich. Dieser Artikel beleuchtet die Impedanzspektren unterschiedlicher Kondensatortechnologien und zeigt, wann welches Verhalten zu erwarten ist.
Üblicherweise lassen sich die frequenzabhängigen elektrischen Eigenschaften von Kondensatoren mithilfe von Impedanz- und Kapazitätsspektren (oder dem S-Parameter) darstellen. Diese wiederum werden von einer Vielzahl von elektrochemischen, physikalischen und anderen technisch relevanten Parametern beeinflusst.
Allerdings ist es nötig, diese von stets vorhandenen Mess-Artefakten sowie von parasitären Effekten zu trennen. Da es manchmal nicht möglich ist, alle Daten im Datenblatt abzubilden, müssen Ingenieure unter Umständen auf gemessene Spektren zurückgreifen, um das geeignete Bauteil für den eigenen Schaltungsentwurf auszuwählen. Um eine bestmögliche Datengrundlage zu schaffen, hat Würth Elektronik eiSos das Online-Tool RedExpert implementiert, das Spektren, aber auch andere Messungen zur Verfügung stellt.
Im Folgenden werden die Charakteristiken solcher Spektren beschrieben und wie sich grundlegende elektrische Eigenschaften daraus ableiten lassen.
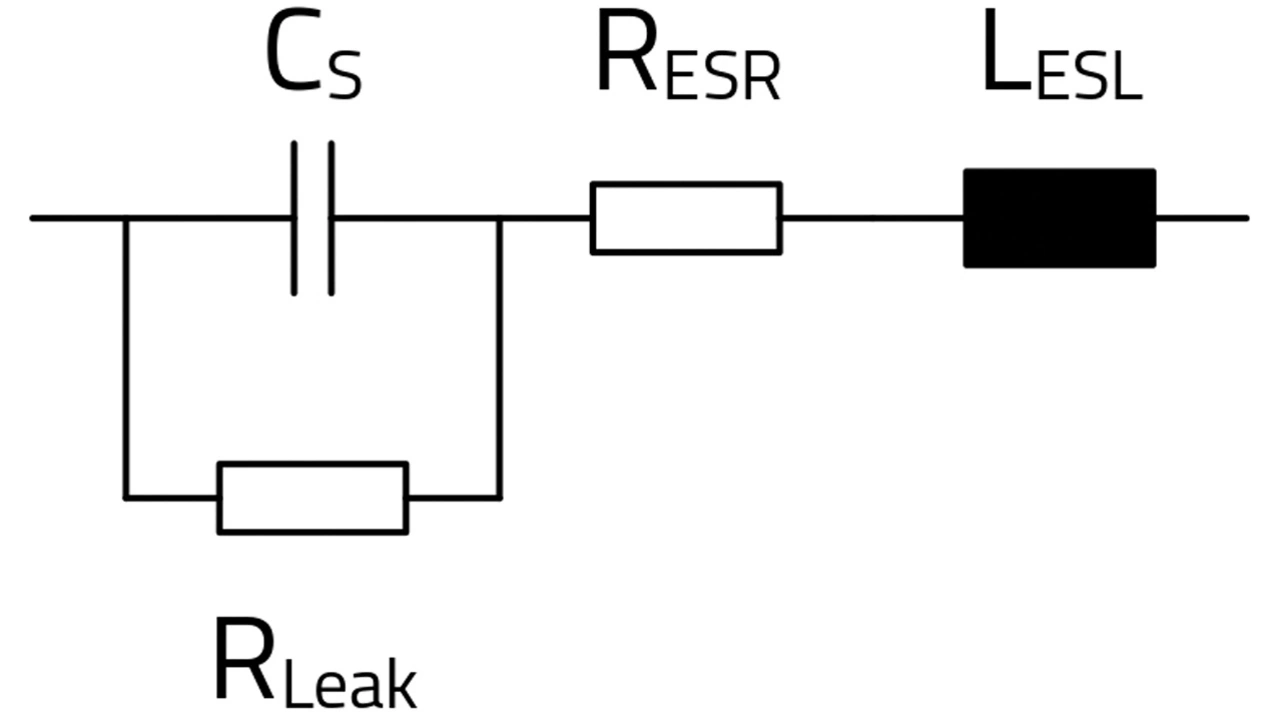
Ersatzschaltung von Kondensatoren
Mit der in Bild 1 gezeigten Schaltung ist es möglich, frequenzabhängige Impedanzspektren aller Kondensatortypen zu modellieren. CS steht dabei für die reine Kapazität, die für sich genommen bei keinem elektrischen Bauteil in seiner reinen Form existiert. Jeder reale Kondensator hat Verluste, die die Aufladung verlangsamen. Dieses Phänomen wird durch den rein ohmschen äquivalenten Serienwiderstand RESR (Equivalent Series Resistance) beschrieben. Der Widerstand des Verbrauchers und der Leitungen tragen ebenfalls zum ESR bei.
Die reine verlustfreie Kapazität CS ist durch das Differenzial folgender Gleichung definiert:
Dabei ist dQ die Ladungsänderung und du die Spannungsänderung am Kondensator.
Jeder Wechselstrom in einem Metallleiter induziert ein magnetisches Feld, das dem Strom entgegenwirkt. In diesem Modell wird diese Eigenschaft durch die äquivalente Serieninduktivität LESL (Equivalent Series Inductance, ESL) beschrieben. Manchmal wird sie auch als parasitäre Induktivität bezeichnet. Anders als CS und RESR ist der Wert der ESL nicht genau definiert und kann sich je nach Messsystem oder Anwendung ändern, da zusätzlich zu den metallischen Elektroden des Kondensators noch Mess- oder Zuleitungen angeschlossen werden.
CS, RESR sowie LESL sind die wichtigsten Parameter, um die Mehrzahl aller Spektren beschreiben zu können. Im einfachsten Ansatz sind sie Konstanten und ändern sich nicht mit der Frequenz. Dies ist für die Elektrotechnik ausreichend genau.
Der Langzeit-Ladungsverlust, auch Leckstrom genannt, lässt sich in guter Näherung durch den rein ohmschen Widerstand RLeak beschreiben. Normalerweise ist RLeak um einige Zehnerpotenzen größer als RESR und kann oft vernachlässigt werden. Wie später noch klar wird, ist seine Wirkung in den Spektren nur bei sehr niedrigen Frequenzen weit unterhalb von 1 Hz sichtbar. Den Leckstrom korrekt zu beschreiben ist jedoch eine physikalisch komplexe Angelegenheit, die von weiteren Parametern wie Vorpolungszeiten (Formierzeit) und Temperatur abhängen kann. Aus messtechnischen Gründen ist es daher häufig üblich, nicht RLeak, sondern den Wert des Leckstroms zusammen mit seinen Messbedingungen im Datenblatt anzugeben.
Die Ersatzschaltung in Bild 1 bietet auch die Möglichkeit, praktisch jede Abhängigkeit von Spannung, Umgebungsbedingungen (z. B. Temperatur) oder nichtlinearer Frequenz zu modellieren. In diesem Fall werden alle Modellparameter durch geeignete mathematische Funktionen ersetzt oder ganze Schaltungsabschnitte durch verzweigte Netzwerke ersetzt.
Impedanz- und Kapazitätsspektren
Der folgende Abschnitt definiert häufig verwendete Begriffe und Messgrößen wie Kapazität und Impedanz. Die Schaltung aus Bild 1 lässt sich als frequenzabhängige komplexe Impedanz Z, Kapazität C, Streuparameter (S-Parameter) S, Dielektrizitätskonstante ε oder jede andere messbare komplexe elektrische Größe beschreiben. Passive Bauelemente werden häufig durch ihre Kapazität und Impedanz charakterisiert. Deshalb liegt im Folgenden der Schwerpunkt auf diesen beiden Größen. Die Impedanz Z ist eine komplexe Größe mit Re(Z) und Im(Z) als Real- bzw. Imaginärteil:
Das Symbol j bezeichnet die imaginäre Einheit, definiert als j² = –1. Häufig wird diese komplexe Impedanz auch durch Betrag |Z| und den Phasenwinkel φ ausgedrückt:
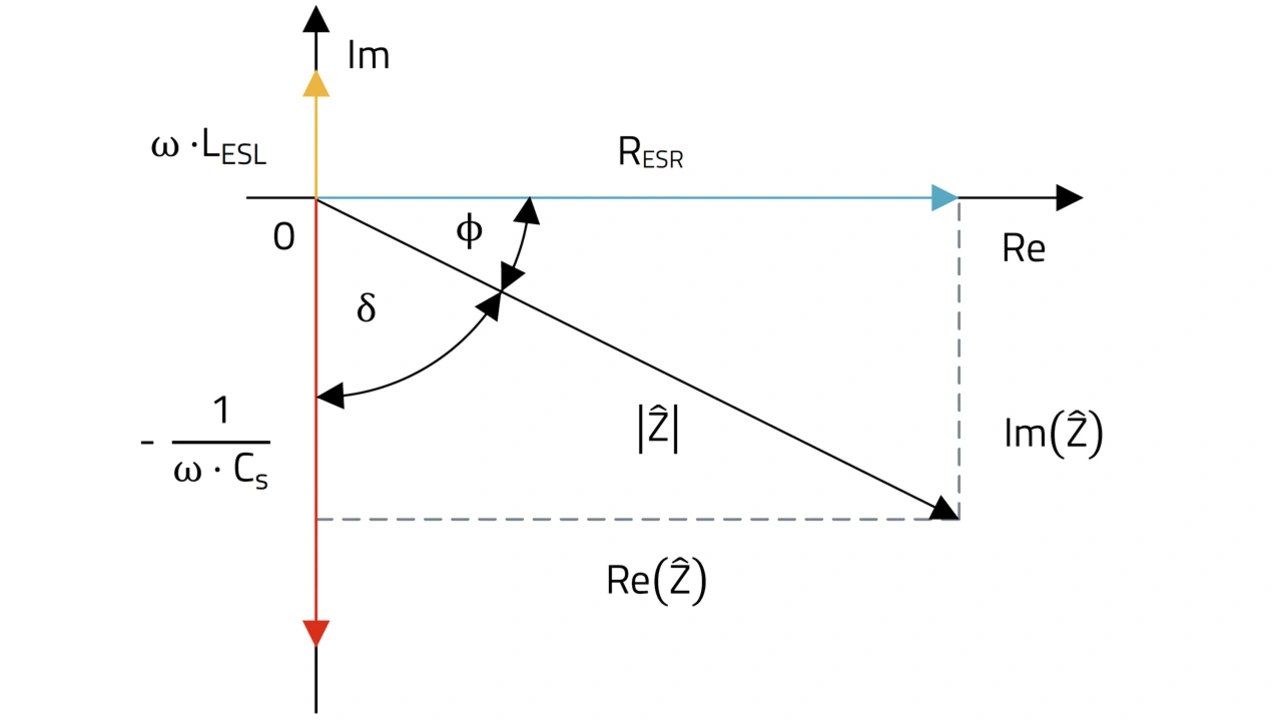
In einer komplexen Ebene (Bild 2) beschreibt φ den Winkel zwischen Re(Z) (Abszisse) und dem komplexen Vektor Z. Physikalisch gesehen stellt |Z| das Verhältnis der Amplituden von Spannung zu Strom dar, während φ die Phasendifferenz zwischen Spannung und Stromstärke bei einer bestimmten Frequenz angibt. Der Phasenwinkel φ ist mit dem Verlustwinkel δ verbunden:
In der Elektrotechnik ist es ebenfalls üblich, |Z| und ihren äquivalenten Serienwiderstand RESR = Re(Z) zu verwenden. Bei dem Beispiel in Bild 1 ist der äquivalente Serienwiderstand der Realteil der Impedanz. Um die Beziehung zwischen dem Modell und der komplexen Größe Z grafisch darzustellen, sind alle Modellparameter (mit Ausnahme von RLeak) auch in Bild 2 angegeben. Die ausführliche mathematische Beschreibung findet sich hier.
Die Impedanz lässt sich mit folgender Gleichung auch in eine komplexe Kapazität umschreiben:
Alle diese Größen wie Re(Z), Im(Z), |Z| oder φ lassen sich mit Impedanz- oder Netzwerkanalysatoren messen. Jedes elektronische Bauteil (nicht nur Kondensatoren) lässt sich durch einen Satz frequenzabhängiger Größen charakterisieren, wie Re(Z) und Im(Z) oder Re(C) und Im(C). Aber erst durch Ersatzschaltungen wie in Bild 1 lassen sich diese Messergebnisse auch interpretieren. Das Modell (auch als Standardmodell bezeichnet) liefert die mathematischen Mittel, um die elektrischen Parameter CS, RESR, LESL und RLeak zu bestimmen. Außerdem eignet sich das Modell dafür, die theoretischen Spektren zu berechnen.
Zwei Praxisbeispiele
Durch Veränderung von CS, RESR, LESL und RLeak lässt sich das grundlegende Frequenzverhalten für alle Kondensatoren berechnen. Dies wird im Folgenden beispielhaft für einen Folien- und einen Superkondensator gezeigt. Die Parameter für die beiden Beispiele sind in Tabelle 1 aufgeführt.
| Parameter | Folienkondensator WCAP-FTBE | Superkondensator WCAP-STSC |
|---|---|---|
| CS | 4,7 µF | 50 F |
| RESR | 5 mΩ | 15 mΩ |
| LESL | 5 nH | 5 nH |
| RLeak | 10 MΩ | 10 MΩ |
Tabelle 1: Für die Berechnung der Spektren verwendete Parameter für den Folienkondensator WCAP-FTBE und den Superkondensator WCAP-STSC
CS, RESR, LESL und RLeak werden als Konstanten und unabhängig von der Frequenz angenommen, was in den meisten Fällen gut mit den Messungen übereinstimmt. Allerdings ist insbesondere für RESR in der Messung eine Frequenzabhängigkeit festzustellen, wie in den folgenden Abschnitten erläutert wird. Wie oben erwähnt, lässt es sich auch umgekehrt betrachten. Es ist bereits mit diesem einzelnen Modell möglich, die Produktparameter aus einer gemessenen Kurve (Bild 3) abzuleiten
Bevor man sich mit gemessenen Graphen beschäftigt, lohnt es sich, einen Blick auf theoretische Graphen zu werfen. Diese haben den Vorteil, dass sie für einen beliebigen Frequenzbereich erstellt werden können, sodass sich alle Merkmale wie zum Beispiel charakteristische Frequenzen in einem Diagramm darstellen lassen.
Im Allgemeinen wird die Position der auffälligsten Stellen in den Spektren durch vier charakteristische Frequenzen beschrieben:
- charakteristische Frequenz des Dämpfungsglieds RESR und CS:
- charakteristische Frequenz des Resonanzkreises LESL und CS:
- charakteristische Frequenz des Dämpfungsglieds RLeak und CS:
- charakteristische Frequenz des Dämpfungsglieds RESR und LESL:
Diskussion der Kurvenverläufe
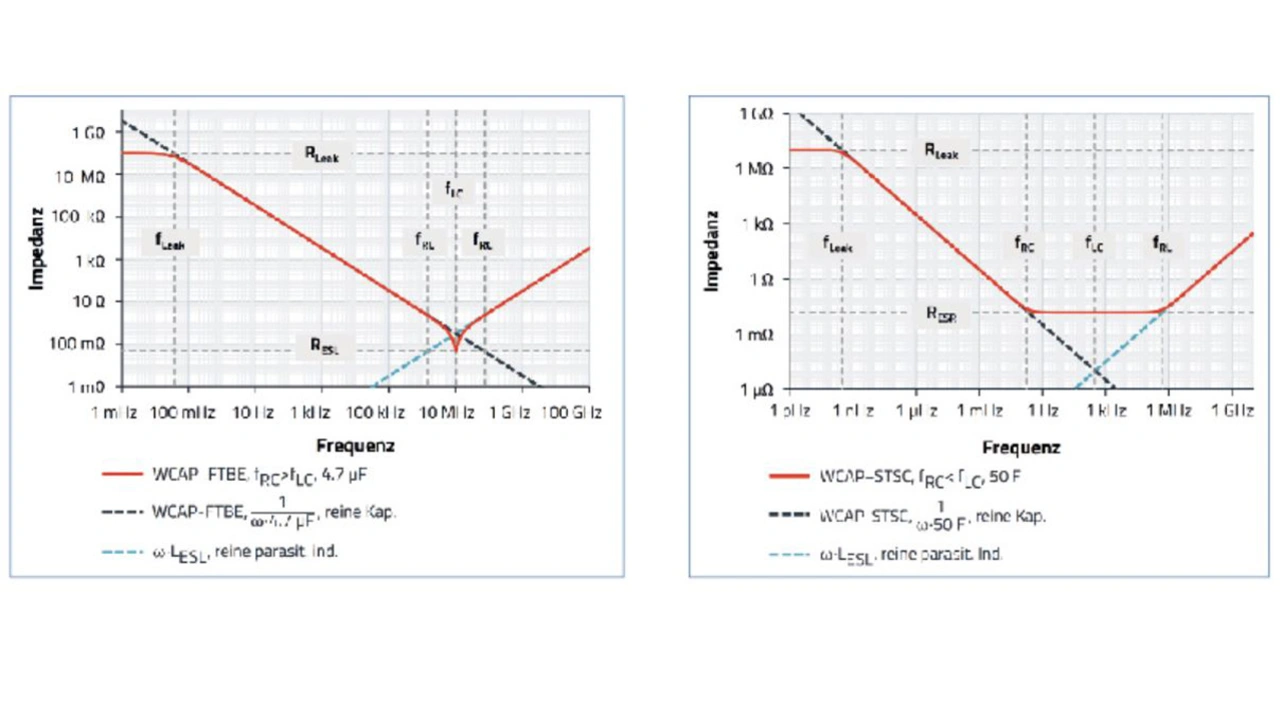
Die schwarzen und blauen gestrichelten Linien in beiden Diagrammen von Bild 3 kennzeichnen den rein kapazitiven und induktiven Teil. Die charakteristische Frequenz fRC des RC-Glieds ist die Frequenz, mit der der Kondensator geladen und entladen werden kann. Der Kehrwert der Frequenz ist im Grunde die Ladezeit bei idealer konstanter Ladespannung.
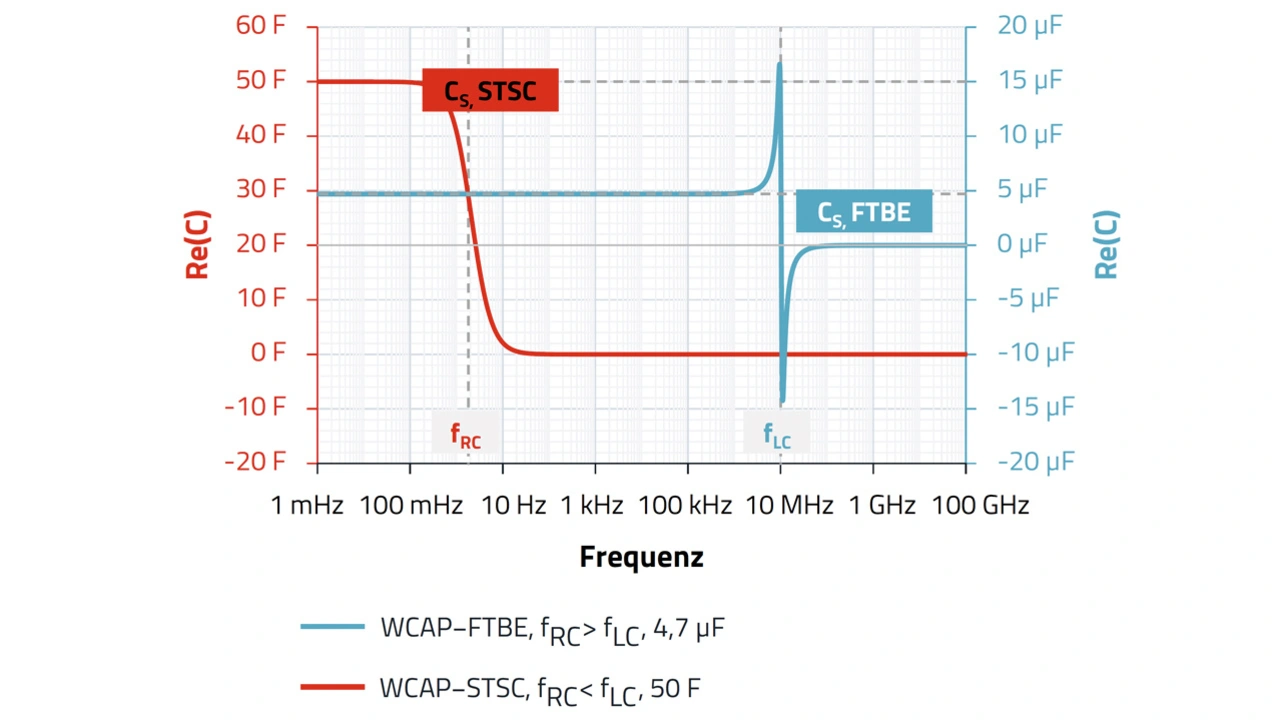
Für den Superkondensator mit 50 F und einem ESR von 15 mΩ beträgt die ideale Ladezeit etwa 5 s. Unterhalb der Frequenz von 0,2 Hz (5 s)-1 kann der Kondensator seine Kapazität nahezu voll ausnutzen (>99,3 Prozent). Oberhalb dieser Frequenz wird der Kondensator nicht mehr vollständig geladen (bezogen auf die maximale Spannung des Signals). Bei fRC zeigt der Superkondensator im Kapazitätsspektrum eine Schulter (rote Linie in Bild 4). Unterhalb dieser Frequenz lässt sich der Kapazitätswert aus dem Diagramm ableiten. Oberhalb von fRC zeigt das Impedanzspektrum ein Plateau mit RESR (Bild 3b).
Die charakteristische Frequenz des LC-Glieds fLC ist die Frequenz, bei der die parasitäre Induktivität und Kapazität in Resonanz sind. Unterhalb dieser Frequenz verhält sich der Kondensator kapazitiv, er kann also elektrische Ladung speichern, oberhalb dieser Frequenz verhält sich der Kondensator induktiv. Die Eigenresonanz führt beim Folienkondensator WCAP-FTBE zu einem scharfen Minimum im Impedanzspektrum (Bild 3a). An diesem Punkt lässt sich der RESR direkt ablesen. Kondensatoren sollten in Anwendungen nicht bei fLC oder oberhalb dieser Frequenz betrieben werden.
Das Kapazitätsspektrum des Folienkondensators FTBE zeigt in Bild 4 (blaue Kurve) einen Pol, der eine Form der Singularität darstellt. Es handelt sich dabei um ein echtes physikalisches Verhalten und nicht nur um ein Mess-Artefakt. Der Prüfling, der aus dem Kondensator und der parasitären Induktivität besteht, verhält sich wie ein Oszillator bzw. Schwingkreis. Im Bereich des stark asymptotischen vertikalen Anstieges bei positiven Kapazitätswerten trägt das Messsignal konstruktiv zu den Schwingungen des Resonators bei.
Das heißt, die Ladungsänderung dQ am Kondensator ist überproportional hoch, obwohl die Größe der angelegten Spannungsänderung du gleich bleibt. Da CS = dQ/du ist, wird eine starke Zunahme der Kapazität gemessen. Beim Maximum befindet sich das System in Resonanz mit der Messfrequenz. Erhöht man die Messfrequenz, wechselt die Kapazität (Singularität) bei fLC abrupt das Vorzeichen. Am negativen Ast des asymptotischen Kapazitätsverlaufes überlagert sich das Messsignal destruktiv mit den Schwingungen des Resonators. Der Strom fließt in Anteilen gegenläufig zur Messspannung. Dadurch führt die angelegte Spannungsänderung du dazu, dass die Ladungsänderung dQ im Kondensator effektiv abnimmt, was zu einer negativen Kapazität führt.
Unterhalb von fLeak, der charakteristischen Frequenz des Dämpfungsglieds RLeak/CS, verhält sich der Kondensator wie ein Widerstand mit dem Wert RLeak. Das heißt, dass bei sehr niedrigen Frequenzen die Leckströme größer sind als der AC-Ladestrom. Normalerweise ist dieser Effekt in den Spektren kaum sichtbar. Er erfordert entweder Messungen bei Frequenzen unter 1 Hz oder einen recht niedrigen Wert von RLeak.
Oberhalb von fRL, der charakteristischen Frequenz des Dämpfungsglieds RESR/L, verhält sich der Kondensator wie eine Induktivität mit dem Wert LESL (Bild 3b). Wenn fRC < fLC ist, beginnt die Impedanz mit der Frequenz wieder zu steigen. Oberhalb von fRL ist es äußerst schwierig, RESR-Werte aus gemessenen Impedanzspektren zu extrahieren.
Die gemessenen Werte der Impedanzspektren würden den Rahmen dieses Artikels sprengen und sind in der Applikationsschrift in Kapitel 2 im Detail beschrieben. Die Untersuchung dort umfasst darüber hinaus auch noch Vielschicht-Keramikkondensatoren (MLCCs) und Aluminium-Elektrolytkondensatoren.
Das könnte Sie auch interessieren
Induktive Bauelemente
Frequenzabhängige Verluste bestimmen
Polymer- und Hybridkondensatoren
Lebensverlängernde Bauteile
Versorgungslage bei passive Bauelementen
»Back to normal – aber nicht überall«
