Leistungswandler - Teil 1
Gekoppelte Induktivitäten und ihre Anwendungen
Fortsetzung des Artikels von Teil 1
Parasitäre Komponenten
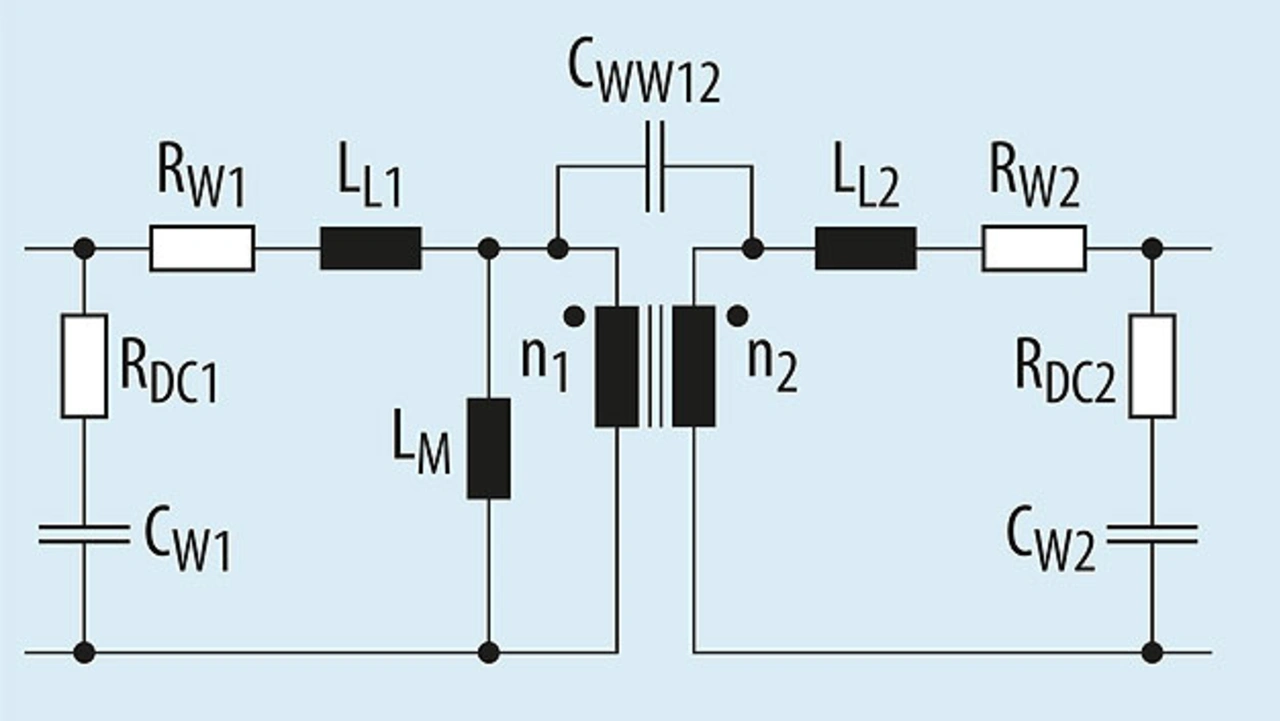
Es gibt eine Reihe von parasitären Effekten, die das Verhalten gekoppelter Induktivitäten beeinflussen. Diese parasitären Effekte sind als Komponenten im Ersatzschaltbild in Bild 5 dargestellt. Die Komponenten in Bild 5 repräsentieren folgende Effekte:
- Streuinduktivität (leakage inductance), LLx,
- Kupferwiderstand der Wicklungen, Rwx,
- Kapazität zwischen den Wicklungen, CWWxy,
- Kapazität zwischen den Windungen (Windung zu Windung), CWx mit RDCx (Verluste im Dielektrikum).
Ein Problem bei der Anwendung der gekoppelten Induktivitäten in Schaltnetzteilen, ist der Umgang mit der Streuflussenergie, die durch die Streuinduktivitäten LLx verursacht wird.
Die Folge davon ist eine Resonanz, die zwischen den parasitären Kapazitäten und der parasitären Induktivität verursacht wird. Durch die Resonanz entstehen hohe Schaltspannungsspitzen über den MOSFETs, die begrenzt werden müssen.
Die Streuinduktivität in gekoppelten Induktivitäten
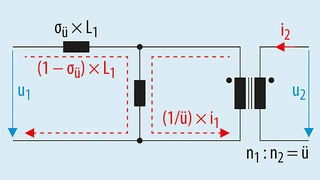
Bei einer gekoppelten Induktivität ist die Gesamtmenge des von einer Wicklung erzeugten magnetischen Flusses nicht vollständig mit der zweiten Wicklung gekoppelt. Jeder magnetische Flussanteil der Primärwicklung, der nicht mit der Sekundärwicklung gekoppelt ist, wirkt als induktive Impedanz in Reihe mit der Primärwicklung. Daher wird diese »Streuinduktivität« im Ersatzschaltbild in Bild 5 als zusätzliche Induktivitäten LL1 und LL2 dargestellt. In html?aid=164807" href="https://www.elektroniknet.de/elektronik/power/bilder/die-streuinduktivitaet-in-gekoppelten-induktivitaeten-bilder-6-9-8199.html?aid=164807">Bild 6 ist zur Verdeutlichung des Streueffektes das Schaltbild einer gekoppelten Induktivität ohne Verluste, jedoch mit Streuinduktivitäten dargestellt.
Der Streufaktor σü ist ein Maß für den Teil des Feldes, der nicht durch beide Wicklungen fließt. Der Streufaktor σü wird wie folgt beschrieben:
σü = 0 bedeutet, dass keine Streuinduktivität vorliegt, und im Fall von σü = 1, dass keine Kopplung zwischen den beiden Wicklungen besteht. Die Induktivität σü × L1 in Bild 6 wird als Streuinduktivität bezeichnet. (1 – σü) × L1 ist die Induktivität, die zur gewünschten Funktion beiträgt. Das Übersetzungsverhältnis der Wicklungen beträgt
Aus Gleichung 10 kann die Gegenkopplungsinduktivität abgeleitet werden:
Damit ergibt sich für die Sekundärinduktivität L2:
Die Streuinduktivität in gekoppelten Induktivitäten, Bilder 6-9
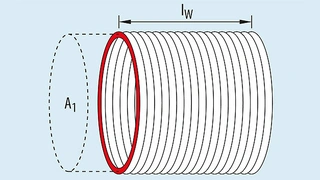
Um zu verstehen, wie die Streuinduktivität in der Praxis minimiert werden kann, müssen die Parameter, die sie beeinflussen, bekannt sein. Die Induktivität einer langen zylindrischen Spule (Bild 7) berechnet sich nach der Gleichung 13,
wobei lW die Länge der Spule ist (html?aid=164807" href="https://www.elektroniknet.de/elektronik/power/bilder/die-streuinduktivitaet-in-gekoppelten-induktivitaeten-bilder-6-9-8199-Bild-2.html?aid=164807">Bild 7).
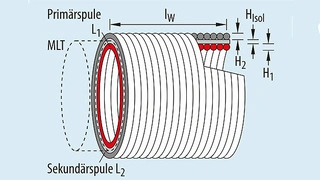
Wenn nun eine zweite Wicklung über die erste gewickelt wird, wie in Bild 8 gezeigt, hat die zweite Wicklung die Induktivität L2:
A1, A2 sind die Flächen jeder einzelnen Wicklung, Ad ist der Flächenunterschied zwischen den beiden Wicklungen. Der Unterschied der Induktivität zwischen den beiden Wicklungen beträgt somit
Die Differenz der einzelnen Spulenflächen kann berechnet werden mit:
MLT ist die durchschnittliche Wicklungslänge, HIsol ist der Abstand zwischen den Wicklungen (Isolierung), H1 und H2 sind die Dicken der Wicklungen 1 bzw. 2.
Die Streuinduktivität ist somit unabhängig vom Kernmaterial und von einem Luftspalt in einem Kern. Hauptfaktoren für die Streuinduktivität sind die geometrischen Unterschiede der beiden Wicklungen.
Zur Minimierung der Streuinduktivität der Spule in Bild 8 muss entweder die Länge der Spule L1 vergrößert werden, oder der Abstand zwischen den Wicklungen muss verringert werden. Daher muss die Fläche A1 der Fläche A2 entsprechen. Das kann z. B. durch bifilares Wickeln der beiden Spulen auf den gleichen Kern erreicht werden.
Bild 9 zeigt verschiedene mögliche Wicklungskonfigurationen. Bei der dargestellten Geometrie ist die am häufigsten verwendete Bauweise eine Sandwich-Konstruktion (Bild 9d), bei der die Sekundärwicklung zwischen der geteilten Primärwicklung gewickelt ist.
Inter-Windungs- und Wicklungskapazitäten
In Bild 5 sind die parasitären Kapazitäten dargestellt. Dazu zählen:
- die Kapazität zwischen den Wicklungen, CWWxy, und
- die Kapazität zwischen den Windungen (Windung zu Windung), CWx mit RDCx.
Die Koppelkapazität zwischen den beiden Wicklungen kann als Plattenkondensator zwischen den beiden Wicklungen betrachtet werden und wird als Wicklungskapazität bezeichnet. Sie kann reduziert werden, indem der Abstand zwischen den Wicklungslagen erhöht wird oder indem die Oberfläche der Wicklungen verringert wird.
Beide Maßnahmen führen jedoch direkt zu einer Erhöhung der Streuinduktivität. Die parasitäre Kapazität zwischen den Windungen stellt sich Windung für Windung ein. Die Kapazität nimmt mit jeder Windung zu. Sie kann durch verschiedene Wicklungstechniken und teilweise durch Verwendung eines Isolationsmaterials mit einer niedrigen Dielektrizitätskonstante für den Draht reduziert werden.
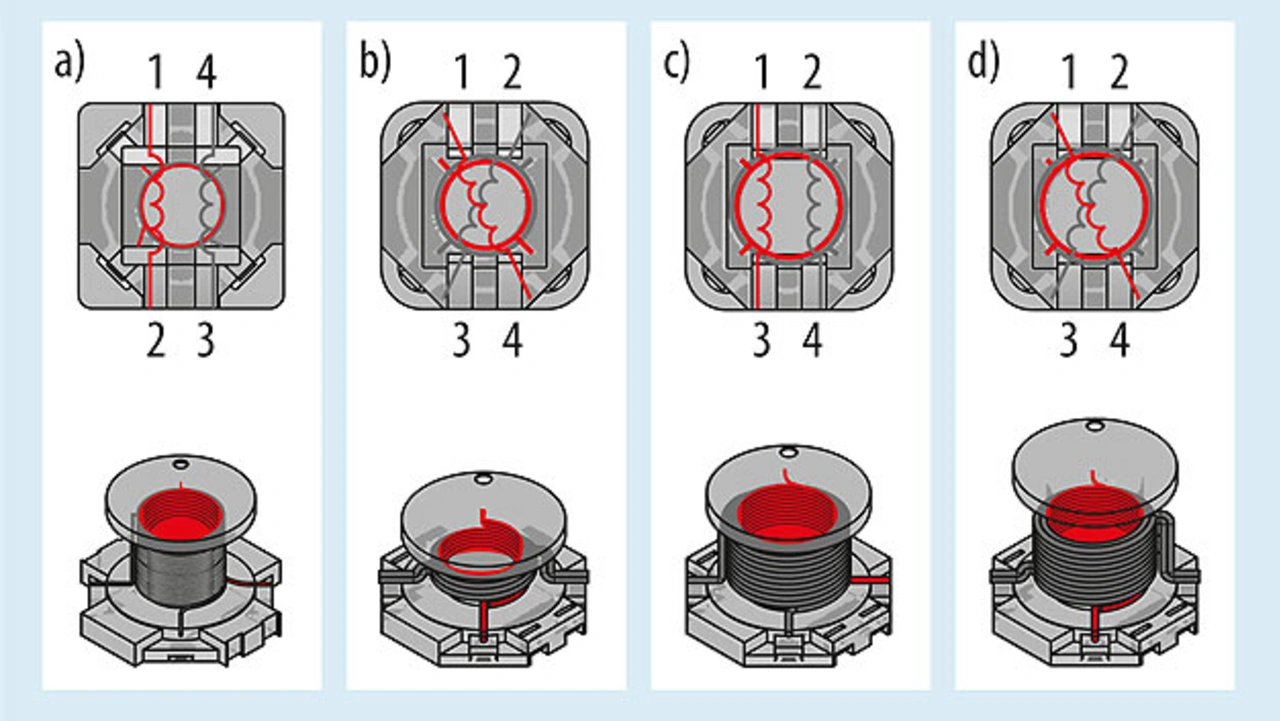
Einige mögliche Wicklungskonstruktionen, sind am Beispiel der gekoppelten Induktivität Würth »WE-DD« in Bild 10 dargestellt. Die bifilar gewickelten Induktivitäten, in den Bildern 10a und 10c dargestellt, haben kein exaktes 1:1-Längen- und damit Übersetzungsverhältnis, da eine zusätzliche 90-°-Umdrehung (eine 1/4-Umdrehung) zum Anschluss-Pin hinzugefügt werden muss.
Die bifilare Wicklung sorgt jedoch für eine enge gegenseitige Kopplung zwischen den Wicklungen, hat aber den Nachteil, dass die Kapazitäten zwischen den Windungen höher werden, was eine niedrigere Resonanzfrequenz zur Folge hat. Die Anschlussfolge in Bild 10a ist anders, da die Wicklungen im Bauelement anders angeordnet werden müssen, um die Längen der Wicklungen gleich und damit die Streuinduktivität gering zu halten.
Die Induktivitäten mit gekreuzten Wicklungen (Bild 10b und 10d) haben separate Schichten für jedes Wicklungspaket und somit ein genaues 1:1-Windungsverhältnis, was eine geringere Streuinduktivität ergibt. Aufgrund der getrennten Wicklungspakete ist die Kapazität zwischen den Wicklungen geringer, aber auch die gegenseitige Kopplung.
Die Bauformen gekoppelter Induktivitäten können je nach Anforderungen und Einsatzbereich sehr unterschiedlich ausfallen. In Bild 11 sind einige verfügbare gekoppelte Induktivitäten von Würth Elektronik dargestellt.
In weiteren Beiträgen werden die verschiedenen Schaltungen von DC/DC-Wandlern wie Abwärts-, Aufwärts-, Sperr-, SEPIC-, ZETA- und Cuk-Wandler – mit gekoppelten Induktivitäten – erläutert, und es werden Anwendungen der Wandlerschaltungen gezeigt.
Der Autor
Dr.-Ing. Heinz Zenkner
hat Elektrotechnik mit Schwerpunkt Hochfrequenztechnik studiert und im Fachbereich Hochfrequenztechnik promoviert. Er ist seit vielen Jahren öffentlich bestellter und vereidigter Sachverständiger für EMV.
Neben zahlreichen wissenschaftlichen Veröffentlichungen tritt Dr. Zenkner auch als Autor in einer Vielzahl von Werken zur EMV in Erscheinung. In seiner beruflichen Laufbahn hat er als Dozent an verschiedenen Universitäten gearbeitet und Seminare an der IHK geleitet.
Seit vielen Jahren beschäftigt er sich mit industrieller Elektronik, von der ersten Idee eines Produktes bis hin zur Serienproduktion.
emc.expert@we-online.com
- Gekoppelte Induktivitäten und ihre Anwendungen
- Parasitäre Komponenten
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
RIKEN Center for Emergent Matter Science
Induktivitäten betreten die Welt der Quantenmechanik
Aktion »Elektronik Leser testen«
Zehn Praxistester für Powermanagement-Baukästen gesucht!
Isolierende Datenkoppler im Vergleich
Bye Bye Optokoppler?
Würth Elektronik eiSos
Ferrite für die EMV
