Implementierung kaskadierter IIR/FIR-Filter
Matlab, der perfekter Helfer
Fortsetzung des Artikels von Teil 1
Z-Transformation des IIR-Filters in n-ter Ordnung
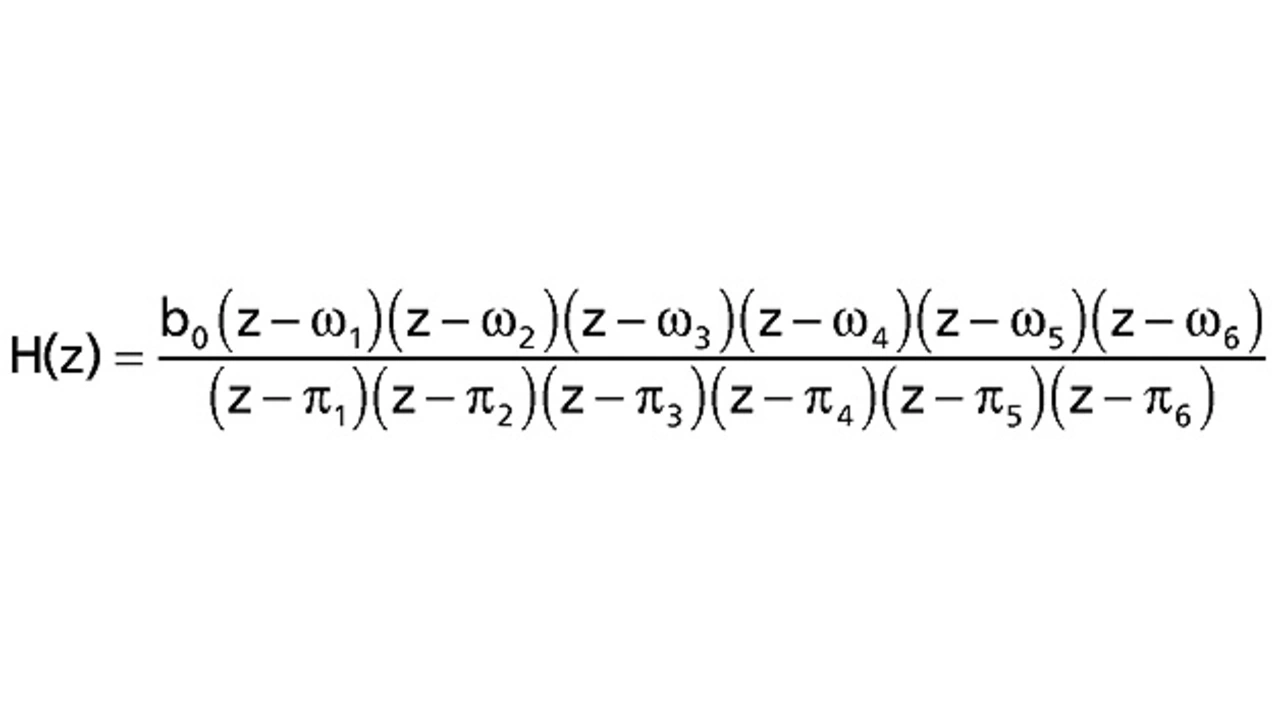
Die erweiterte Transferfunktion für ein IIR-Filter 6ter Ordnung ist in Gleichung (3) gegeben, wobei die Feed-Forward-Koeffizienten die Nullstellen (ω) und die Feedback-Koeffizienten die Pole (π) des Filters repräsentieren.
Jobangebote+ passend zum Thema
Die n+1 Koeffizienten des IIR-Filters n-ter Ordnung werden dann mit Hilfe der roots()-Funktion in Matlab in Faktoren mit Nullstellen und Polen zerlegt. Für das Beispiel-Filter ergeben sich die in Tabelle 3 zu sehenden Pole/Nullstellen.
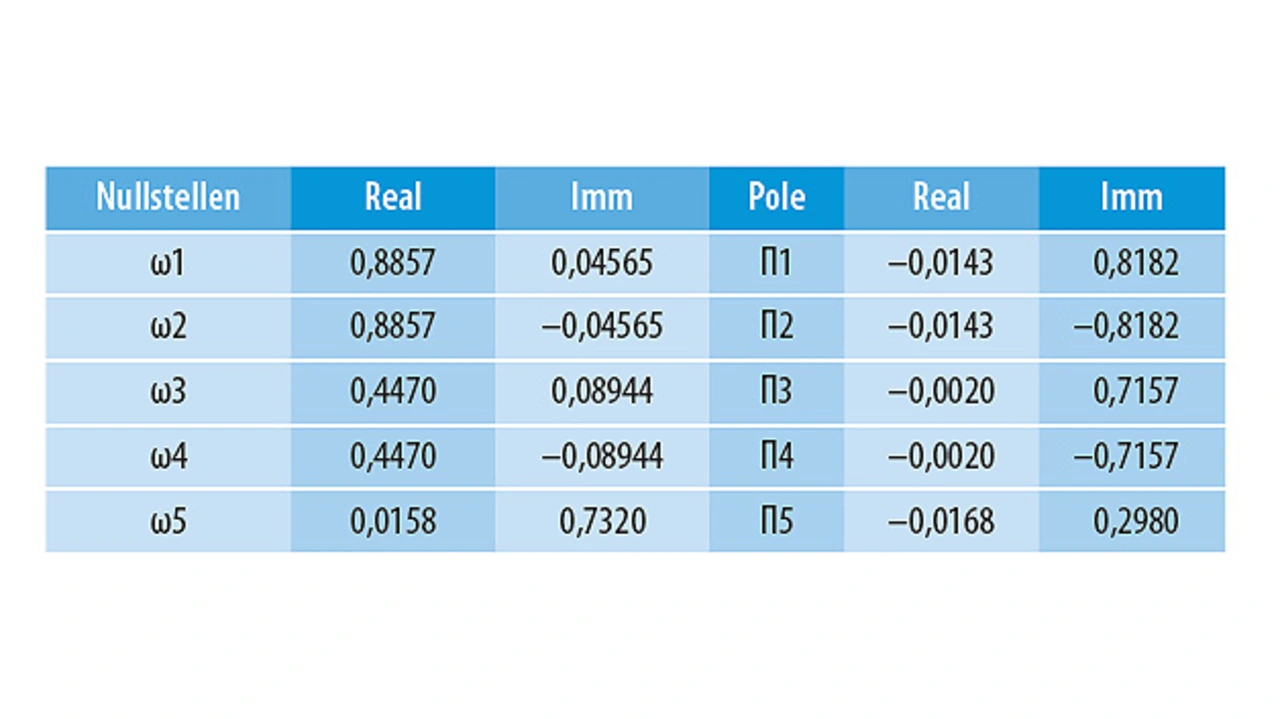
3. Verteilung der Nullstellen/Pole
Nun müssen die Nullstellen/Pole auf die zwei DecFilter-Instanzen verteilt werden. Im Beispiel gibt es drei konjugierte Paare komplexer Wurzeln für Pole und Nullstellen. Das Filter als IIR zweiter Ordnung wird implementiert, gefolgt von einem IIR vierter Ordnung. Auf zwei DecFilter-Blöcken sind folgende Kombinationen möglich: 2×4, 4×2 und 3×3. Die Verteilung der Pole und Nullstellen gestaltet sich ganz einfach: Man multipliziert die gewählten Faktoren aus Gleichung (3) und führt das getrennt für Pole und Nullstellen durch.
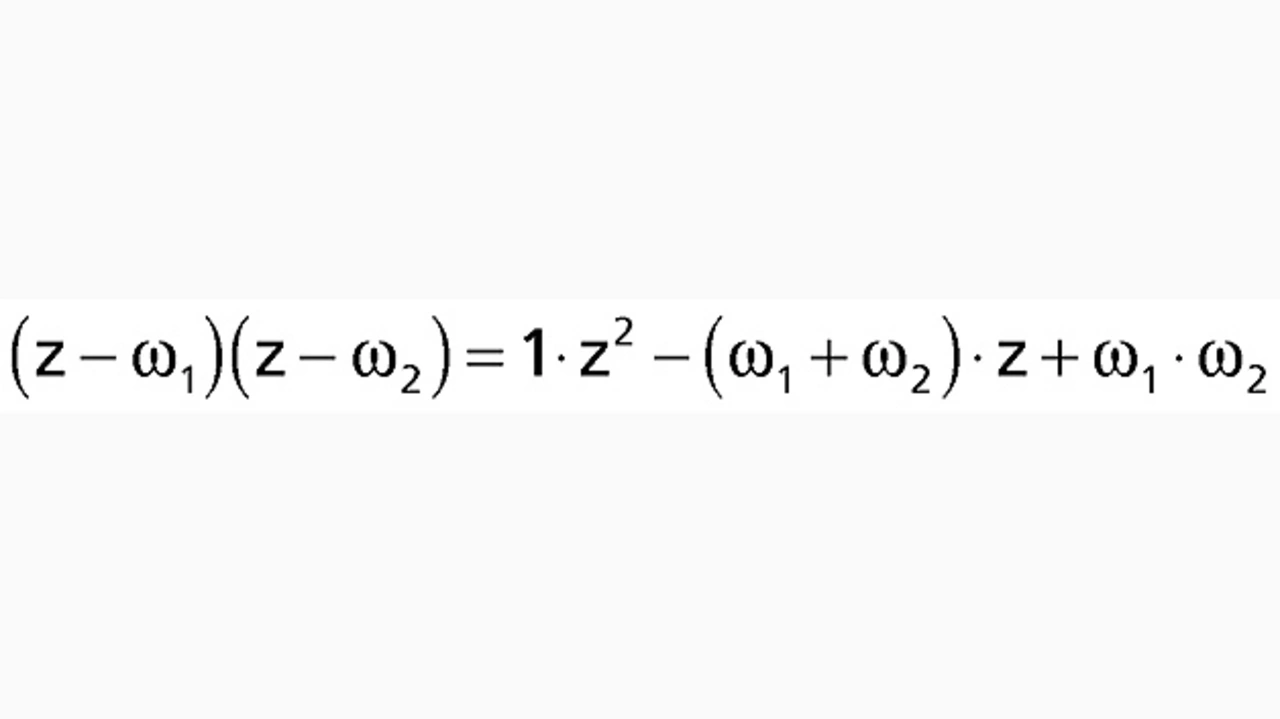
Für das Filter zweiter Ordnung werden ω1/ω2 und π1/π2 kombiniert, um die drei Nullstellen-Koeffizienten zu erhalten. Im beiliegenden Matlab-Beispiel wird das manuell erledigt (4).
Aus Gleichung (4) kommen die Koeffizienten für die erste Stufe:
Nicht immer gibt es ein gut definiertes Verfahren für die Kombination von Polen/Nullstellen, mit dem sich das gewünschte Ergebnis erreichen lässt. Für kleine Filter reicht es üblicherweise aus, gezielte Trial-and-Error-Versuche“ anzustellen, bis sich eine Lösung findet.
Für das IIR-Filter vierter Ordnung wird die gleiche Methode herangezogen, um zwei Sätze von Polynomen zwei 2ter Ordnung zu gewinnen. Dann kommt die Matlab-conv()-Funktion zum Einsatz, um per Polynom-Multiplikation das Polynom vierter Ordnung zu erhalten. Die Frequenzantworten der IIR-Filter zweiter Ordnung (erste Stufe) und vierter Ordnung (zweite Stufe) sind in Bild 3 a+b dargestellt.
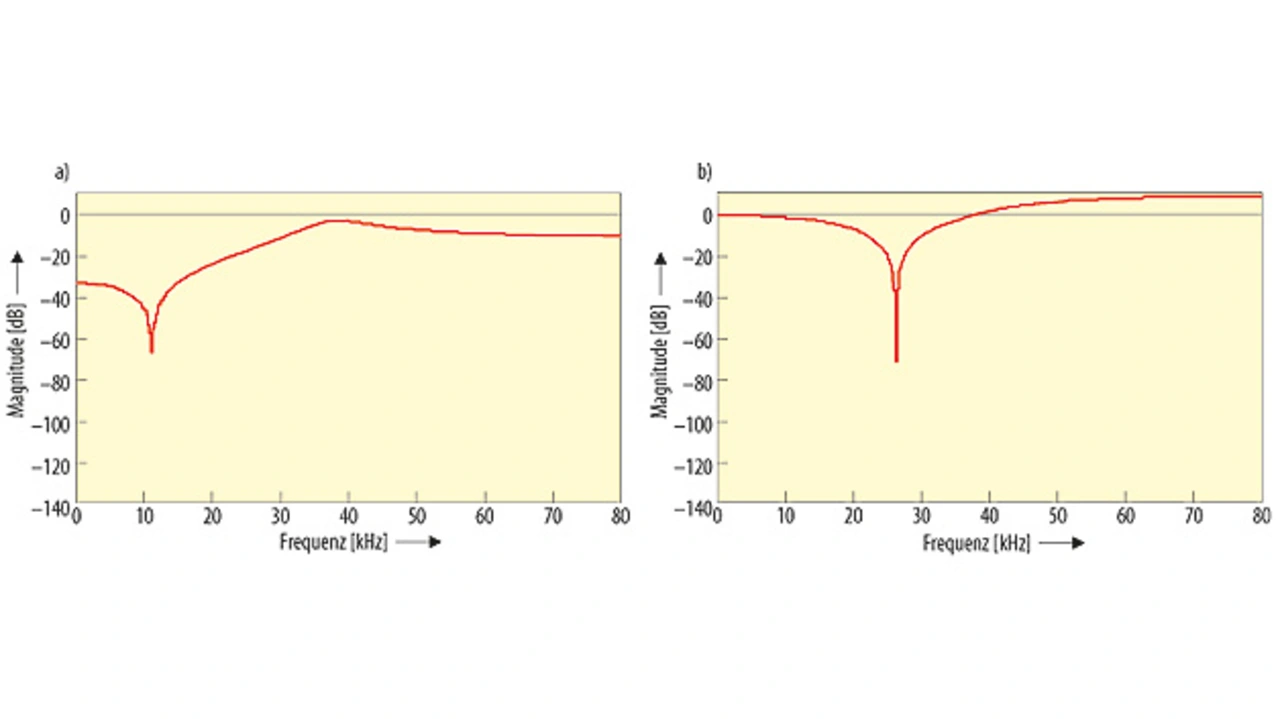
Wichtig ist es hier, auf die Reihenfolge zu achten, nach der die Teilfilter kaskadiert werden. Es muss beachtet werden, dass die Verstärkung der zweiten Stufe größer als eins ist. Würde diese Stufe vorne angeordnet werden, so würde die zweite Stufe überlaufen. Um das zu vermeiden, müssten die Filterkoeffizienten skaliert werden. Umgekehrt gilt: Dämpft die erste Stufe im Durchlassbereich um 10 dBb, dann wird das in der zweiten Stufe kompensiert, um im Durchlassbereich insgesamt eine Verstärkung von eins zu erreichen. Es muss darauf geachtet werden, in der oder den ersten Stufen eines kaskadierten Filters nicht zu stark zu dämpfen.
Bild 4 zeigt die kombinierte Frequenzantwort der zwei Filter. Man kann sehen, dass diese der Frequenzantwort des ursprünglichen Filters sechster Ordnung entspricht.
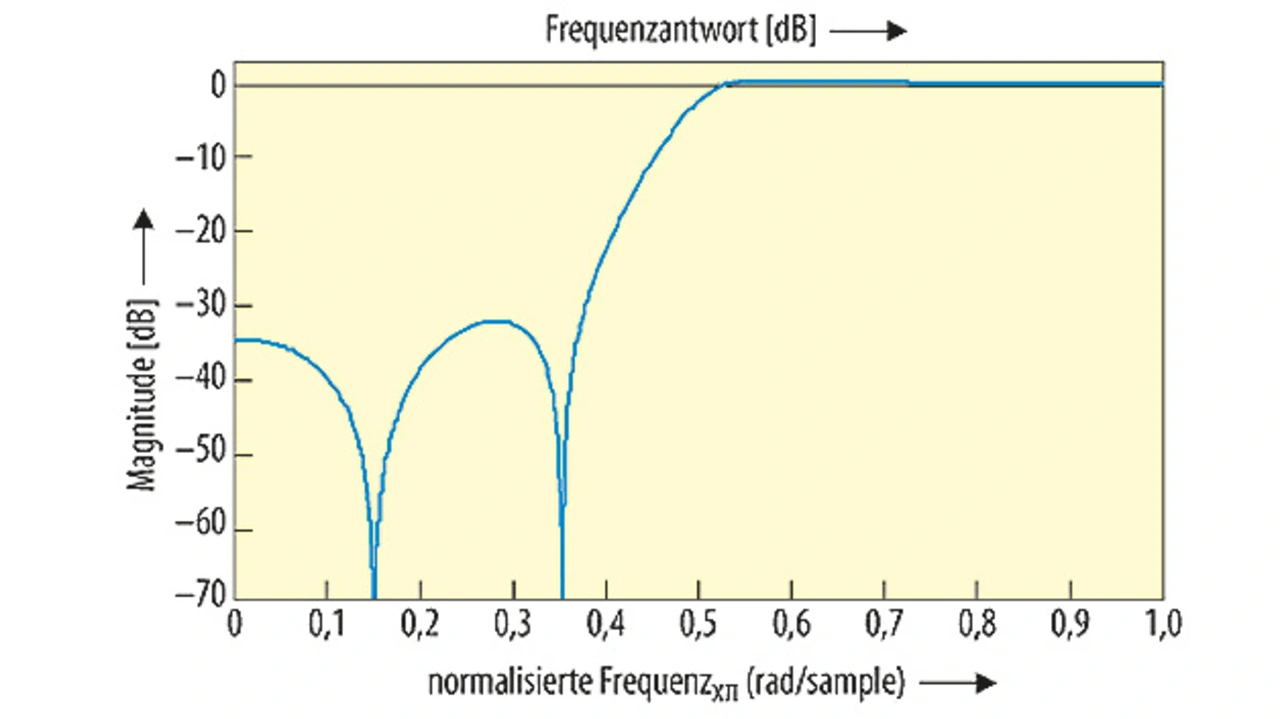
Im letzten Schritt wird die Stabilität der Filter analysiert und untersucht, ob diese gemäß der Spezifikation funktionieren. Für das vorgebene Beispiel wird das mit Hilfe der Matlab-Funktionen dfilt() (Ddiscrete-Ttime Filter) und fvtool() (Open Filter Visualization Tool) durchgeführt. Daraus ergibt sich ein Plot der Pole/Nullstellen, mit dessen Hilfe die Frequenzantwort und Stabilität des Filters geprüft werden können.
Nach der Implementierung in Hardware verhält sich das Filter möglicherweise aufgrund der Festkomma-Repräsentation anders als das Matlab-Filter. Erfüllt das Filter nach der Implementierung die Spezifikation nicht, so kann es notwendig werden, die Leistungsdaten des Filters zu verbessern, um die Unzulänglichkeiten der Implementierung auszugleichen.
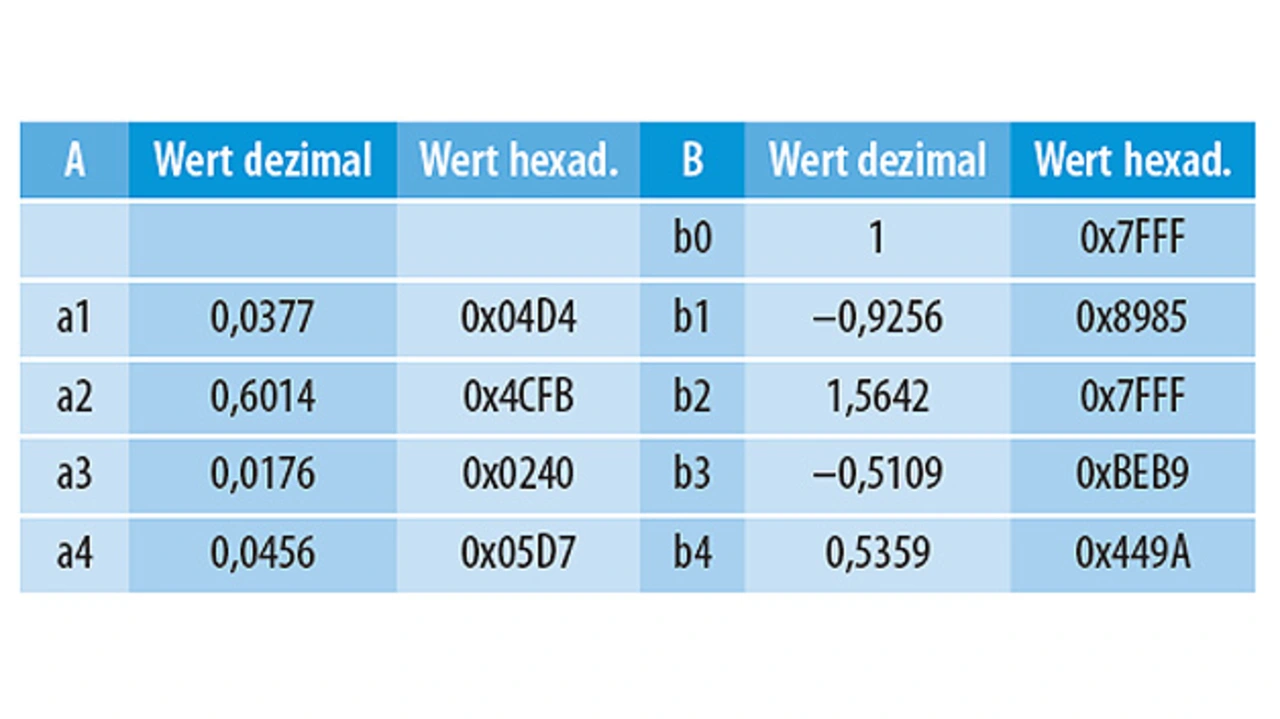
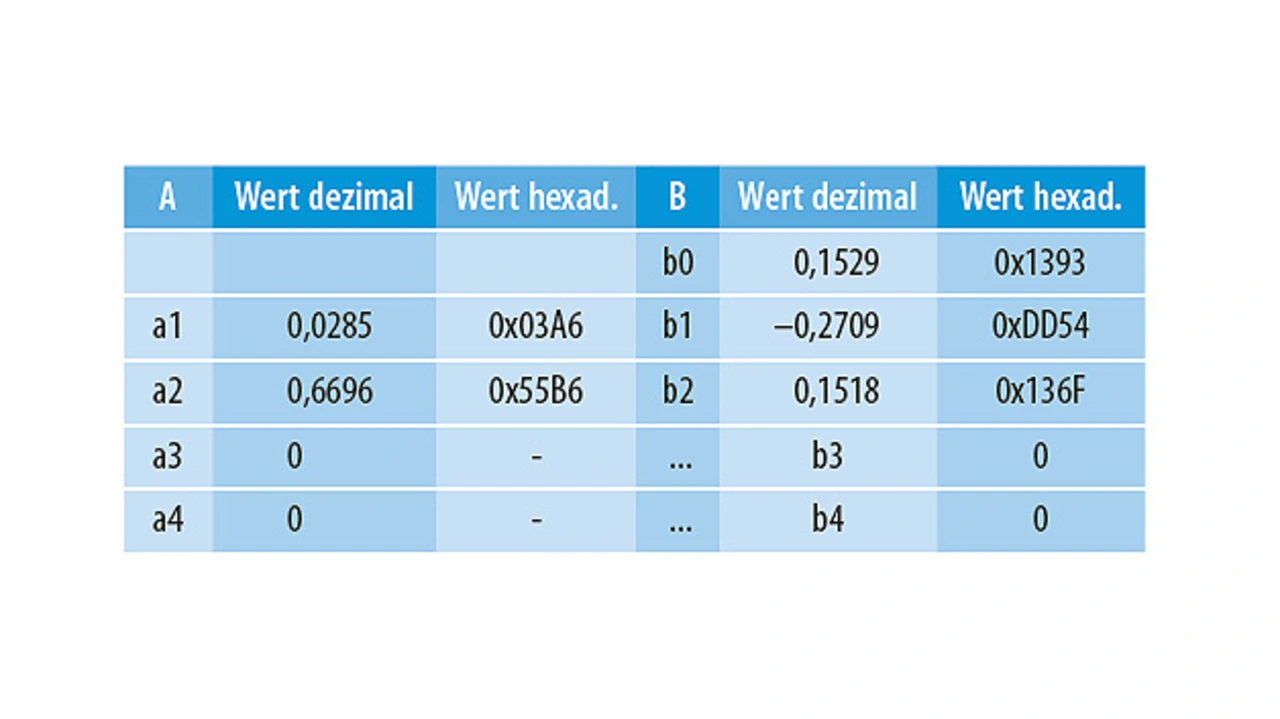
Während in Tabelle 4 die relativen Koeffizienten für die erste Instanz des DecECFilterILTER-Blocks (IIR zweiter Ordnung) aufgelistet sind, zeigt Tabelle 5 die relativen Koeffizienten für die zweite Instanz des DecECFilterILTER-Blocks (IIR vierter Ordnung).
Man beachte, dass b0=1, da eine Verstärkung=1 für die zweite Stufe angesetzt ist.
Der Autor
|
Mark Stachew |
|---|
|
hat einen Abschluss in Elektrotechnik der Universität von Idaho mit einem weiterführenden Diplom in VLSI-Studien. 2000 trat Stachew in den Halbleiterbereich von Motorola ein und arbeitete im Entwurf von Mixed-Signal-Automotive-Mikrocontrollern. Im Jahr 2008 verlagerte sich seine Tätigkeit in Richtung Analog-IP und Design digitaler Signalverarbeitungsarchitektur für Mixed-Signal-SoCs. Er ist derzeit bei NXP Semiconductors im Systems Engineering tätig, wo er sich auf Radar-HF- und Basisband-Prozessor-Integration, Lidar, digital moduliertes Ultrabreitband-Radar und die gesamte elektronische Steuersystemarchitektur für Fahrer-unterstützende und automatisierte Fahrzeuge konzentriert. |
- Matlab, der perfekter Helfer
- Z-Transformation des IIR-Filters in n-ter Ordnung
- Matlab-Beispiel-Code
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Ingenieur-Berechnungen
Matlab 2016a mit interaktivem Editor
Software für Infotainment-Systeme
Komplexität beherrschen
Entwicklungssystem
Testautomatisierung mit dem Debugger
Mentor Graphics
General Motors nutzt Capital Design-Werkzeuge
ISSCC 2016 in San Francisco
Baukasten zum autonomen Fahren
Automotive Ethernet Congress 2016 in München
Wie Ethernet das Auto verändert
Fahrerassistenzsysteme und Infotainment
Highlights auf der CES 2016
Elektronik Produkte des Jahres 2016
Die Top 10 der Rubrik Automotive
