Startseite > Power > Spannungswandler > Einfacher mit Spitzenstromregelung

Leistungsfaktorkorrektur

Einfacher mit Spitzenstromregelung

26. Juni 2023, 6:00 Uhr | Bosheng Sun

▶ Diesen Artikel anhören

Fortsetzung des Artikels von Teil 1

Spitzenstromregelung für PFC-Stufen im lückenden Betrieb

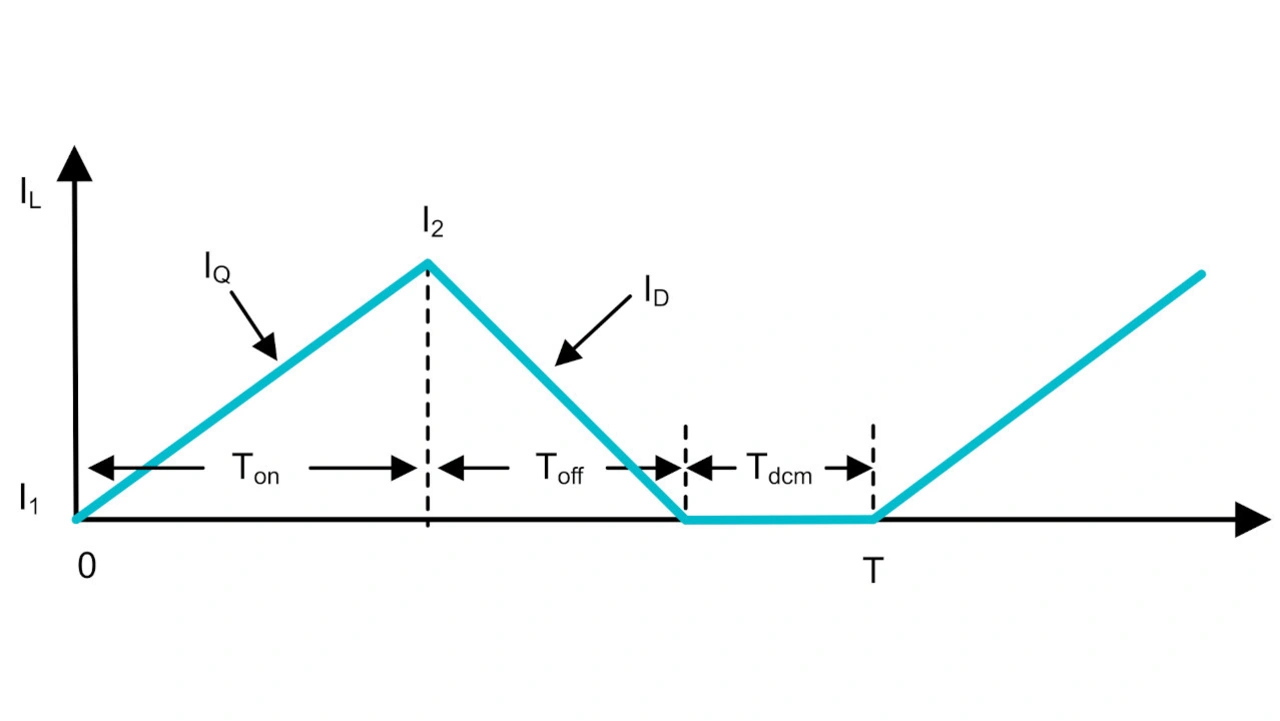
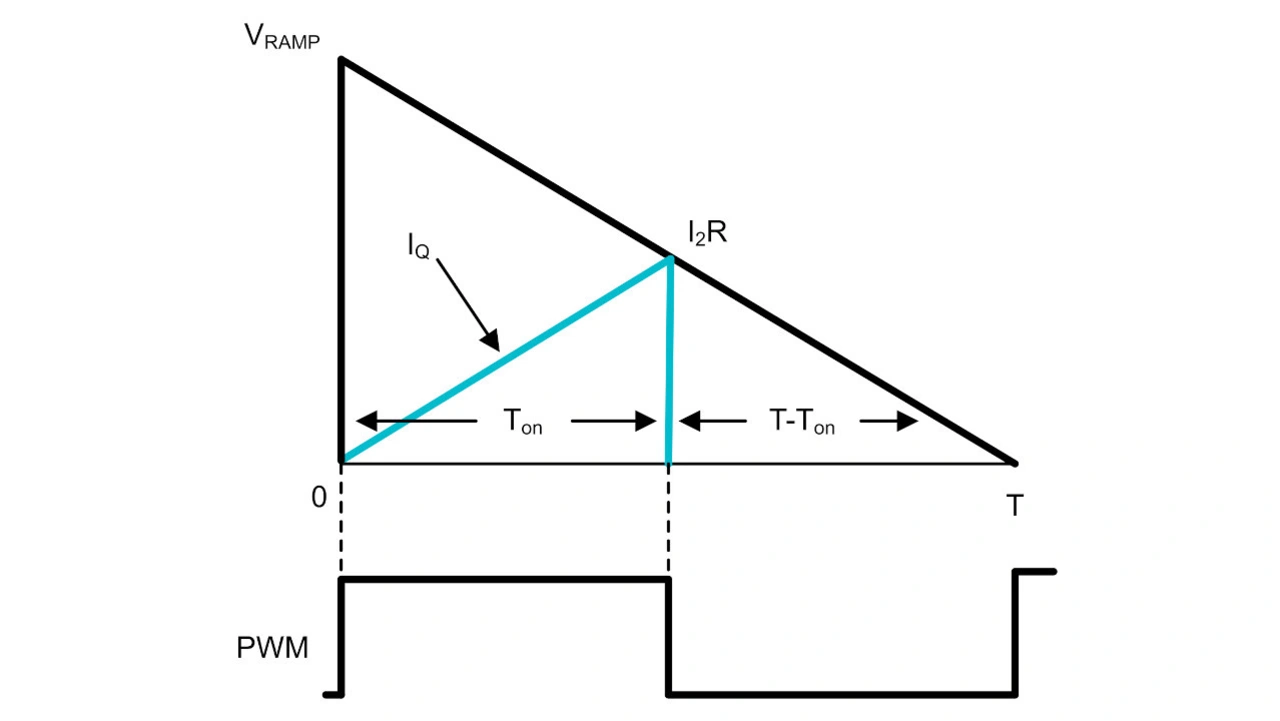
Der gleiche Algorithmus lässt sich auch auf den lückenden Betrieb (DCM, Discontinuous Conduction Mode) anwenden. Bild 5 zeigt den Verlauf des Spulenstroms im DCM-Betrieb. Der Spulenstrom fällt am Ende von T_aus auf Null und bleibt für den Rest der Periode T_dcm auf Null; daher ist T = T_ein + T_aus + T_dcm. Der PWM-Generator ist derselbe wie in Bild 4, aber die PWM-Aus-Zeit ist T_aus + T_dcm, nicht T_aus, wie in Bild 6 gezeigt.

Matchmaker+ Anbieter zum Thema

zu Matchmaker+

Durch Umformulierung von Gleichung 4 in Gleichung 9 wird der durchschnittliche Strom im DCM für einen Schaltzyklus berechnet:

$I subscript M W end subscript equals open parentheses I subscript text 2 end text end subscript minus fraction numerator U subscript E cross times T subscript e i n end subscript over denominator 2 cross times L end fraction close parentheses cross times fraction numerator T subscript e i n end subscript plus T subscript a u s end subscript over denominator T end fraction space space space space space left parenthesis 9 right parenthesis$

Im eingeschwungenen Zustand muss der magnetische Fluss in jedem Schaltzyklus ausgeglichen werden, was zu Gleichung 10 führt:

$U subscript E cross times T subscript text ein end text end subscript equals open parentheses U subscript A minus U subscript E close parentheses cross times T subscript a u s end subscript space space space space space left parenthesis 10 right parenthesis$

Aufgelöst nach T_aus und in Gleichung 9 eingesetzt ergibt sich:

$I subscript M W end subscript equals open parentheses I subscript 2 minus fraction numerator U subscript E cross times T subscript e i n end subscript over denominator 2 cross times L end fraction close parentheses cross times fraction numerator T subscript e i n end subscript cross times U subscript A over denominator T cross times open parentheses U subscript A minus U subscript E close parentheses end fraction space space space space space left parenthesis 11 right parenthesis$

Aus Gleichung 6 ergibt sich somit Gleichung 12:

$fraction numerator I subscript 2 cross times R over denominator U subscript S _ S Z end subscript end fraction equals fraction numerator T minus T subscript e i n end subscript over denominator T end fraction text (12) end text$

Gleichung 13 berechnet den Spitzenwert des Sägezahnsigals U_{S_SZ} wie folgt:

$U subscript S _ S Z end subscript equals open square brackets fraction numerator G subscript U cross times U subscript E cross times T cross times open parentheses U subscript A minus U subscript E close parentheses over denominator T subscript e i n end subscript cross times U subscript A end fraction plus fraction numerator R cross times T subscript e i n end subscript cross times U subscript E over denominator 2 cross times L end fraction close square brackets cross times fraction numerator T over denominator T minus T subscript e i n end subscript end fraction space space space space space left parenthesis 13 right parenthesis$

Durch Einsetzen von Gleichung 13 in Gleichung 12 und Auflösen nach I₂ ergibt sich Gleichung 14:

$I subscript 2 equals fraction numerator G subscript U cross times U subscript E cross times T cross times open parentheses U subscript A minus U subscript E close parentheses over denominator R cross times T subscript e i n end subscript cross times U subscript A end fraction plus fraction numerator T subscript e i n end subscript cross times U subscript A over denominator 2 cross times L end fraction text (14) end text$

Wird nun I₂ in Gleichung 11 eingesetzt, so erhält man Gleichung 15:

$I subscript M W end subscript equals open square brackets fraction numerator G subscript U cross times U subscript E cross times T cross times open parentheses U subscript A minus U subscript E close parentheses over denominator R cross times T subscript e i n end subscript cross times U subscript A end fraction plus fraction numerator T subscript e i n end subscript cross times U subscript E over denominator 2 cross times L end fraction minus fraction numerator U subscript E cross times T subscript e i n end subscript over denominator 2 cross times L end fraction close square brackets cross times fraction numerator T subscript e i n end subscript cross times U subscript A over denominator T cross times open parentheses U subscript A minus U subscript E close parentheses end fraction I subscript text MW end text end subscript equals G subscript U over R cross times U subscript E space space space space space left parenthesis 15 right parenthesis$

In Gleichung 15 ist G_U im stationären Zustand konstant; daher ist I_MW proportional zu U_E und folgt dem zeitlichen Verlauf von U_E. Wenn U_E eine Sinuskurve ist, ist auch I_MW eine Sinuskurve, wodurch ein Leistungsfaktor von Eins erreicht wird.

Die Gleichungen 9 bis 15 gelten sowohl für CCM als auch für DCM. Wenn also der Spitzenwert des Sägezahnsignals gemäß Gleichung 13 erzeugt wird, ist es möglich, sowohl für CCM als auch für DCM einen Leistungsfaktor von 1 zu erreichen.

Gleichung 1 ist ein Spezialfall von Gleichung 13, bei dem T = T_ein + T_aus. Für Anwendungen mit geringer Last – die PFC-Stufe arbeitet bei geringer Last im DCM-Modus –, bei denen THD und Leistungsfaktor nicht wichtig sind, kann Gleichung 1 zur Vereinfachung der Implementierung verwendet werden.

Testergebnisse

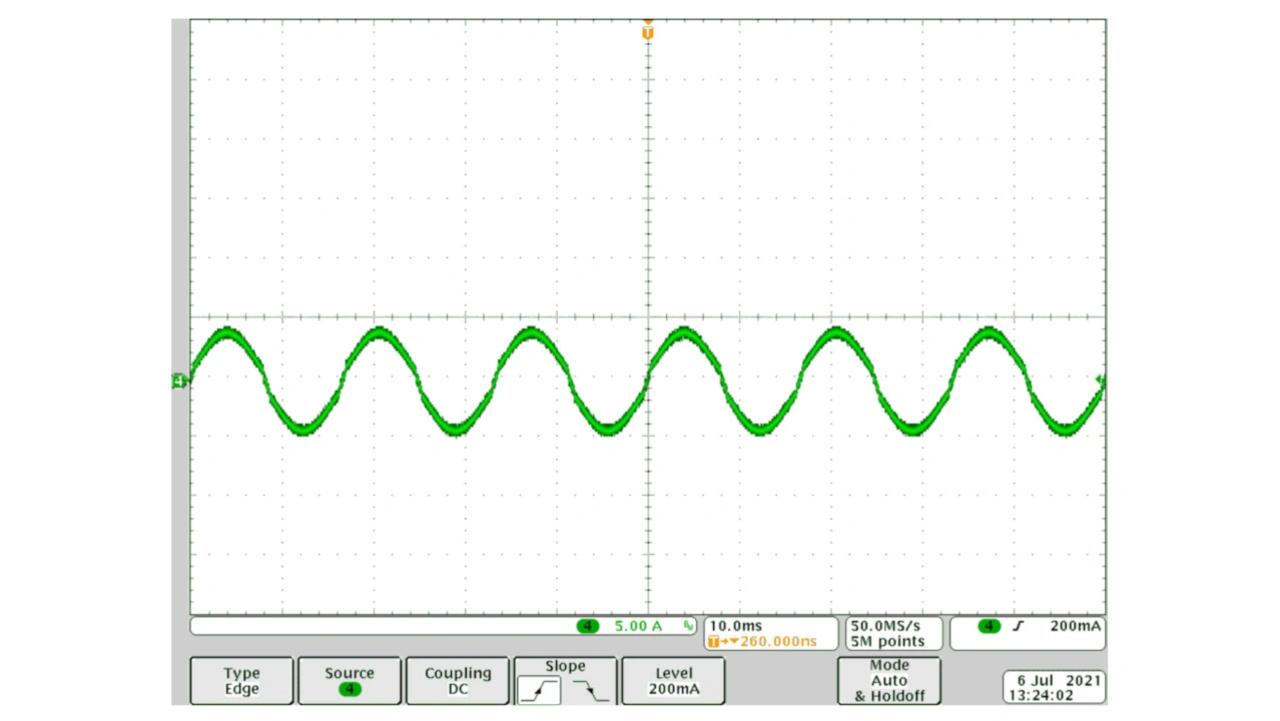
Die neue PFC-Methode mit Spitzenstromregelung wurde an einem Evaluierungsmodul (EVM) für eine 360-W-PFC-Stufe überprüft. Bild 7 zeigt den gemessenen Eingangsstrom, der einen guten sinusförmigen Verlauf aufweist.

Diese neue Methode der Spitzenstromregelung für PFC-Stufen hat viele Vorteile im Vergleich zur traditionellen Mittelwertstromregelung. Der PFC-Controller kann auf der Sekundärseite des AC/DC-Wandlers platziert werden, um einen kombinierten Controller mit dem DC/DC-Wandler einzusetzen und Kosten zu reduzieren. Die Eliminierung des Strommesswiderstands und der von ihm verursachten Leistungsverluste verbessert den Wirkungsgrad. Der durch den Einsatz von Stromwandlern bei niedrigen Tastverhältnissen hervorgerufene Fehler in der Signalrückkopplungsschleife entfällt, was zu einer Verbesserung des Klirrfaktors führt.

Die Spitzenstromregelung für PFC-Stufen lässt sich mit C2000-Mikrocontrollern und dem digitalen Controller für DC/DC-Wandler UCD3138 leicht implementieren.

Der Autor

Bosheng Sun

beendete 1995 sein Elektrotechnikstudium an der Tsinghua-Universität in Peking, China, mit dem Bachelor-Abschluss und 2003 mit dem Master-Abschluss an der Cleveland State University in Ohio, USA. Im Jahr 2003 startete er seine berufliche Laufbahn bei Core Technologies und wechselte 2004 zu Plug Power. Seit 2006 arbeitet Sun bei Texas Instruments an leistungsfähigen Controller-ICs für Leistungswandler. Er ist Inhaber von vier U.S.-Patenten.