Integrierte bidirektionale Messbrücke
HF-Leistung und Rückflussdämpfung bestimmen!
Fortsetzung des Artikels von Teil 3
Der Signalpfad
Bild 8 zeigt Bild 7 mit den zugehörigen Signalen in (Standard) Vorwärtskonfiguration: die Bezugsebene der Wanderwellen steht lastseitig. Bei kleinen Frequenzen mit relativ langen Wellenlängen im Vergleich zur physikalischen Struktur, sind die Spannungen und Ströme phasengleich: die Schaltung kann mit dem Ohmschen Gesetz analysiert werden.
Jobangebote+ passend zum Thema
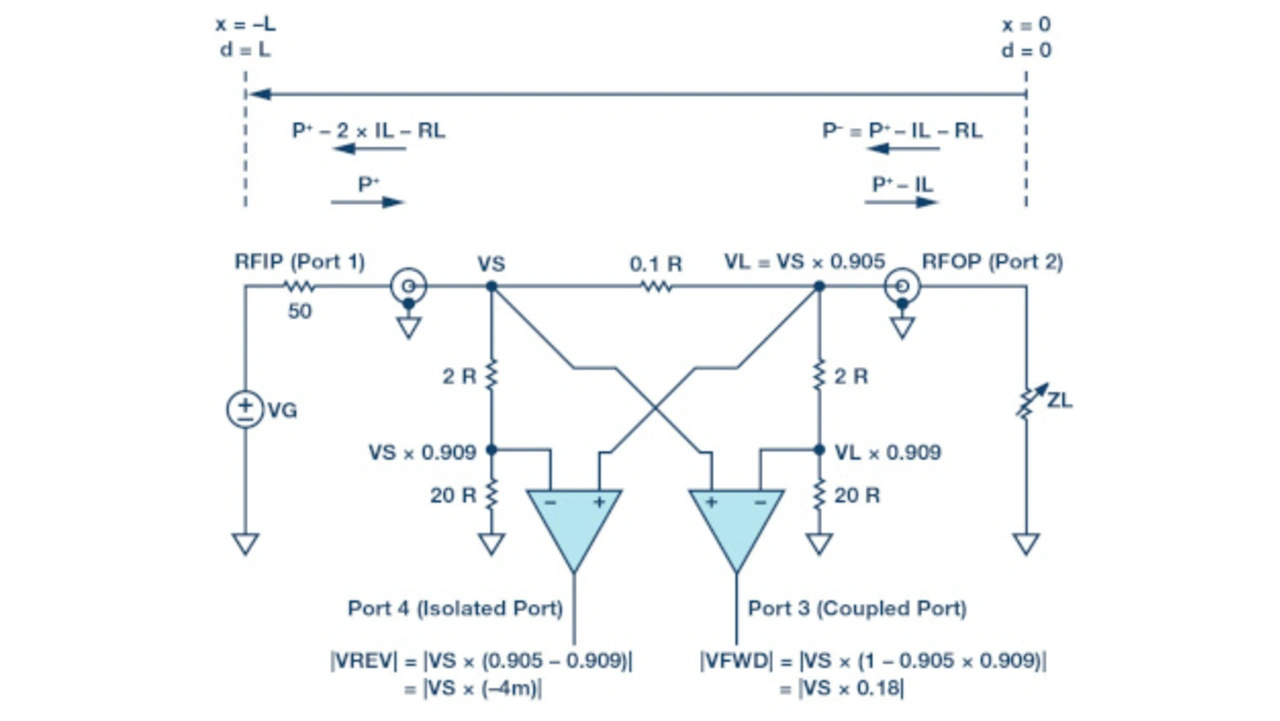
Die Ports liegen wie gezeigt mit dem Eingang (Port 1) bei RFIP, dem Ausgangs (Port 2) bei RFOP, der Kopplung (Port 3) bei VFWD und der Isolation (Port 4) bei VREV. Mit der symmetrischen Struktur liegen die Ports invertiert, wenn ein Signal an ZL reflektiert oder an RFOP angelegt wird. Im Falle einer angepassten Last und einer an Port 1 (RFIP) angelegten Generatorspannung sowie mit ZS = ZL = Z0 = R = 50 Ω, gilt:
| VL = VS+* ZOUT / (ZOUT + 0,1 R) | (16) |
| ZOUT = ZL || (2 R +20 R) = R || 22 R = (22/23) R | (17) |
Dabei entspricht VL/VS+ der Einfügungsdämpfung IL in dB:
| IL = -20 log10(|S21|)= -20 log10(L1) = 0,87 dB | (18) |
Der Dämpfungsfaktor für die beiden Shunt-Zweige, auf jeder Seite des Widerstands der Hauptübertragungsstrecke von 0,1R, errechnet sich zu:
| α = 20 R / (20 R + 2 R) = 20 / 22 = 0,909 | (19) |
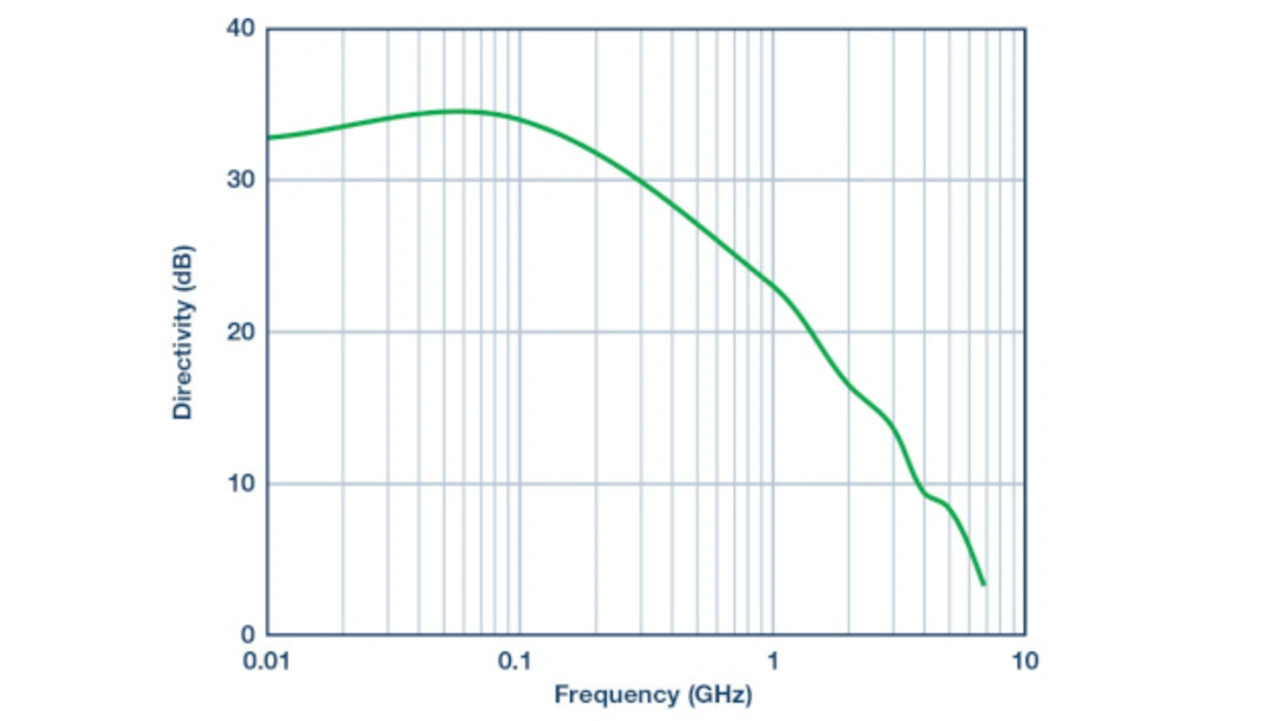
Die Gleichungen in Bild 8 für |VREV| und |VFWD| zeigen die Werte dieser Spannungen bei einem in Vorwärtsrichtung angelegten Signal. Diese Gleichungen belegen für den vereinfachten Schaltplan eine fundamentale Begrenzung der Richtcharakteristik: die Ursache ist die reale Übersprechdämpfung (nur ~ 33 dB Unterdrückung) gegenüber dem isolierten Port.
| D = 20 log10(|VCPL|/|VISO|) = 20 log10 (|0,18|/|-0,004|) = 33 dB | (20) |
Aus Bild 8 ergibt sich auch die Richtwirkung der bidirektionalen Brücke in der linearen Domäne:
| DL = ( 1 - L1 α ) / ( L1 - α ) | (21) |
Um die Richtwirkung zu optimieren, muss α der Einfügedämpfung LI entsprechen. Auf dem Silizium fällt die Richtwirkung üblicherweise besser aus, als durch das Schaltbild suggeriert (Bild 9). Im Normalfall ZL != Z0 ergeben sich die komplexen Spannungen der gekoppelten und isolierten Ports:
| VCPL = VS+(1 - L1 α) + VL-(L1 - α) | (22) |
| VISO = VL-(1 - L1 α) + VS+(L1 - α) | (23) |
Hier bezeichnet VS+ die Vorwärtsspannung an Port 1 (Knoten VS) und VL– die reflektierte Spannung am Port 2 (Knoten VL). Θ kennzeichnet die unbekannte Phasenlage des reflektierten Signals.
| VL- = VS+ L1 |Γ0| exp(jΘ) | (24) |
Anschließend wird in (22) und (23) VL– durch (24) substituiert und mit (21) das Ergebnis vereinfacht:
| VFWD = VS+(1 - L1 α) | (25) |
Daraus resultieren die komplexen Ausgangsspannungen:
| VCPL = VFWD (1 + L1 |Γ0| exp(jΘ)/DL) | (26) |
| VISO = VFWD (L1 |Γ0| exp(jΘ) + 1/DL) | (27) |
Aus (26) und (27) ergibt sich für DL >> 1:
| (28) |
In ADL5920 bilden zwei Linear-in-DBrms-Detektoren von 60 dB Bandbreite die Spannungen VREV und VFWD in jene RMS-Werte VRRMS und VFRMS ab, die (VISO/VSLP) und (VCPL/VSLP) auf der dB-Skala entsprechen.
Der differenzielle Ausgang des Bausteins VDIFF in dB repräsentiert
| VDIFF / VSLP = (VRRMS - VFRMS) / VSLP= (VL1 + V|Γ0|) / VSLP | (29) |
mit einer Detektorflanke VSLP von rund 60 mV/dB. Mit dem Volt-nach-dB-Mapping aus (29) ergibt (28)
| 20log10(VRRMS/VSLP) - 20log10(VFRMS/VSLP)=20log10(L1) + 20log10 |Γ0| | (30) |
und Einsetzen von Gleichung (9) in Gleichung (30) liefert
| PREV - PFWD = – IL - RL | (31) |
| RL = PFWD - PREV - IL | (32) |
.
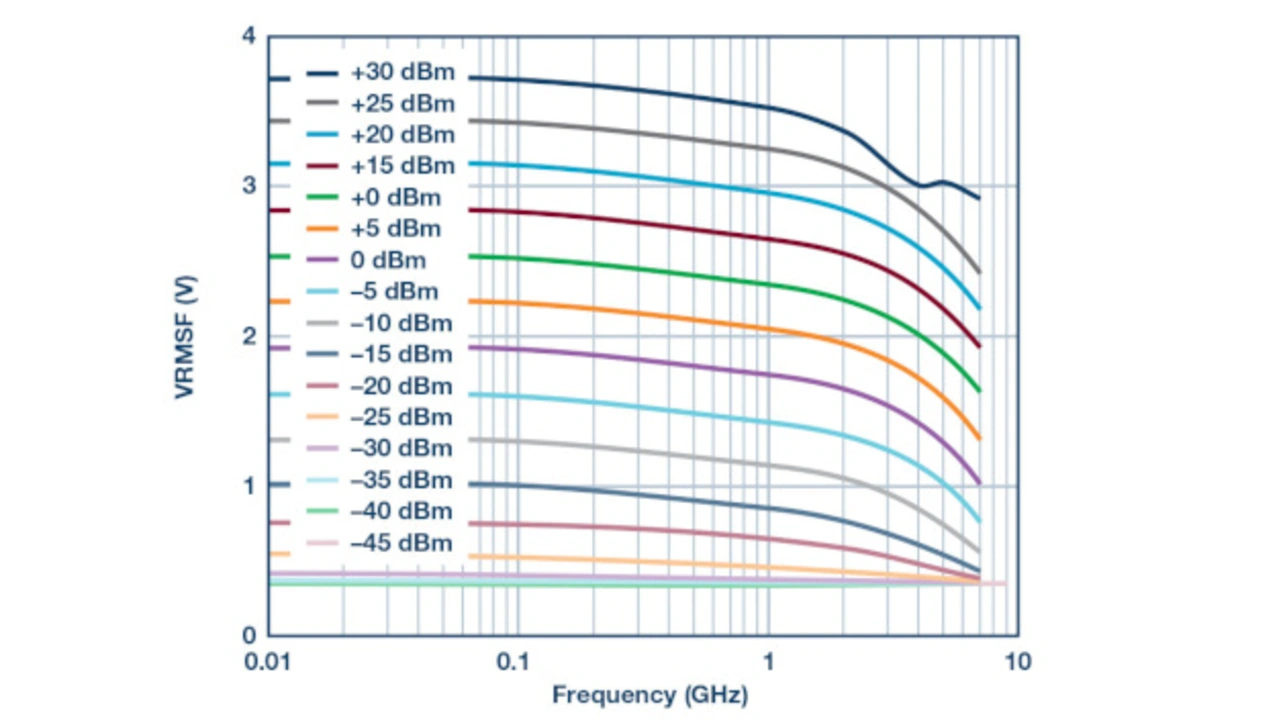
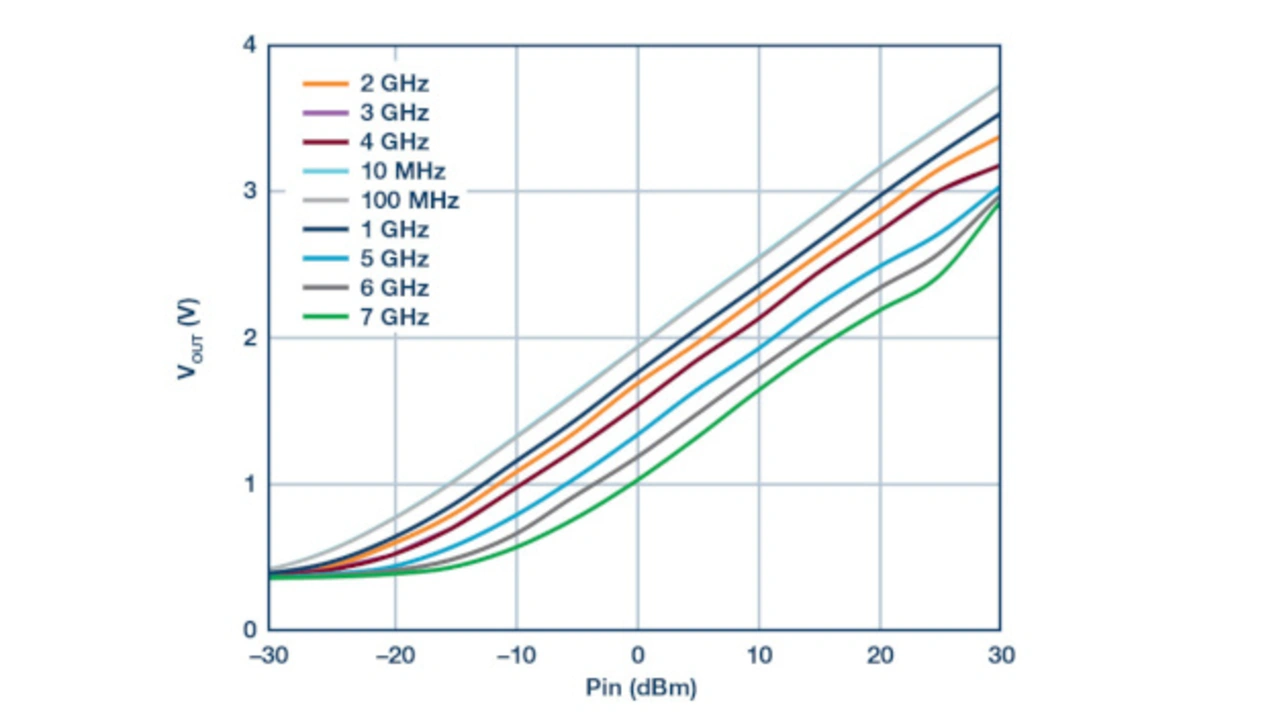
Jede Kurve repräsentiert für einen definierten Leistungspegel die Ausgangsspannung, abhängig von der Frequenz. Während die Darstellung bei 10 MHz endet, wurde der Betrieb bei Frequenzen bis hinunter zu 9 kHz verifiziert. Bild 11 zeigt dieselben Daten als Ausgangsspannung in Abhängigkeit von der Eingangsleistung: jede Kurve zeigt eine andere Frequenz.
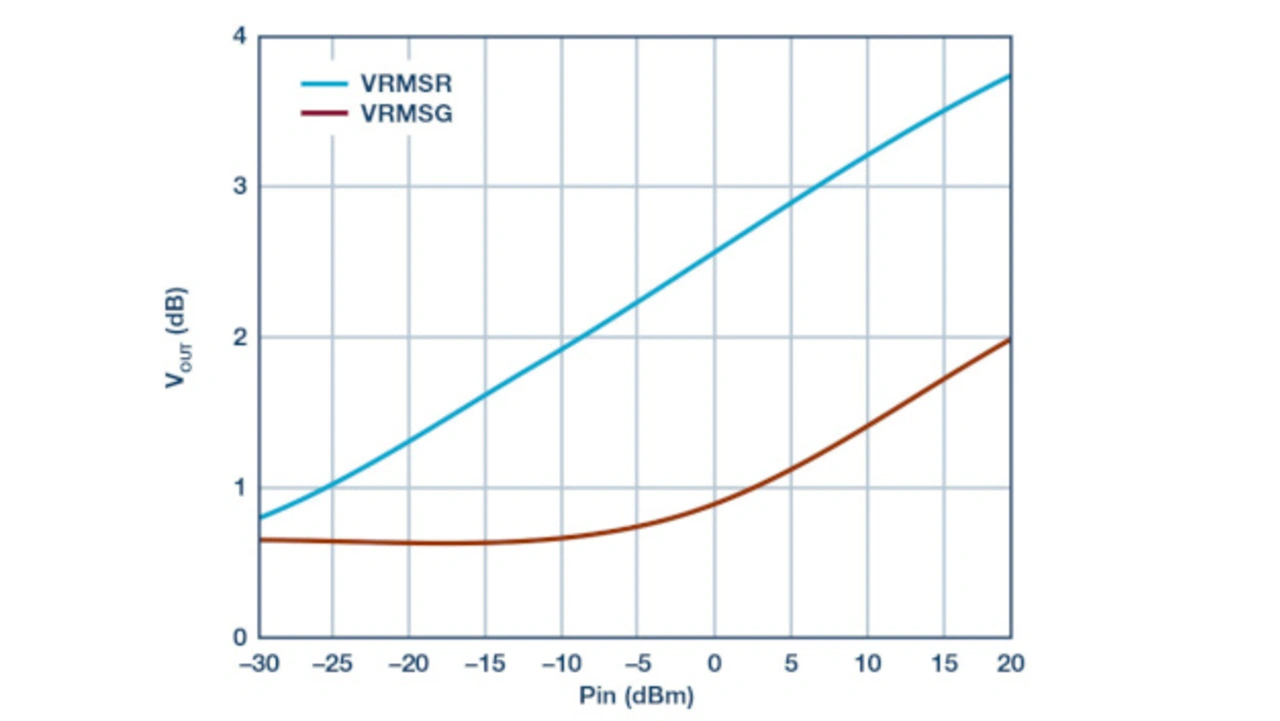
Wird der Pin RFOUT mit einem 50-Ω-Widerstand abgeschlossen, sollte die Reflexion verschwinden. Damit sollte der Detektor im rücklaufenden Pfad auch keine rückwärts laufende Leistung registrieren. Wegen der realen und frequenzabhängigen Richtcharakteristik wird allerdings ein Signalanteil im Rückwärtspfad auftreten. Bild 12 zeigt die gemessene Spannung der Detektoren im Vorwärts- und Rückwärtspfad bei 500 MHz, wenn RFIN durchgestimmt wird und RFOUT mit 50 Ω abgeschlossen ist. Die vertikale Trennung dieser Kurven steht in direktem Verhältnis zur Richtcharakteristik der Brücke.
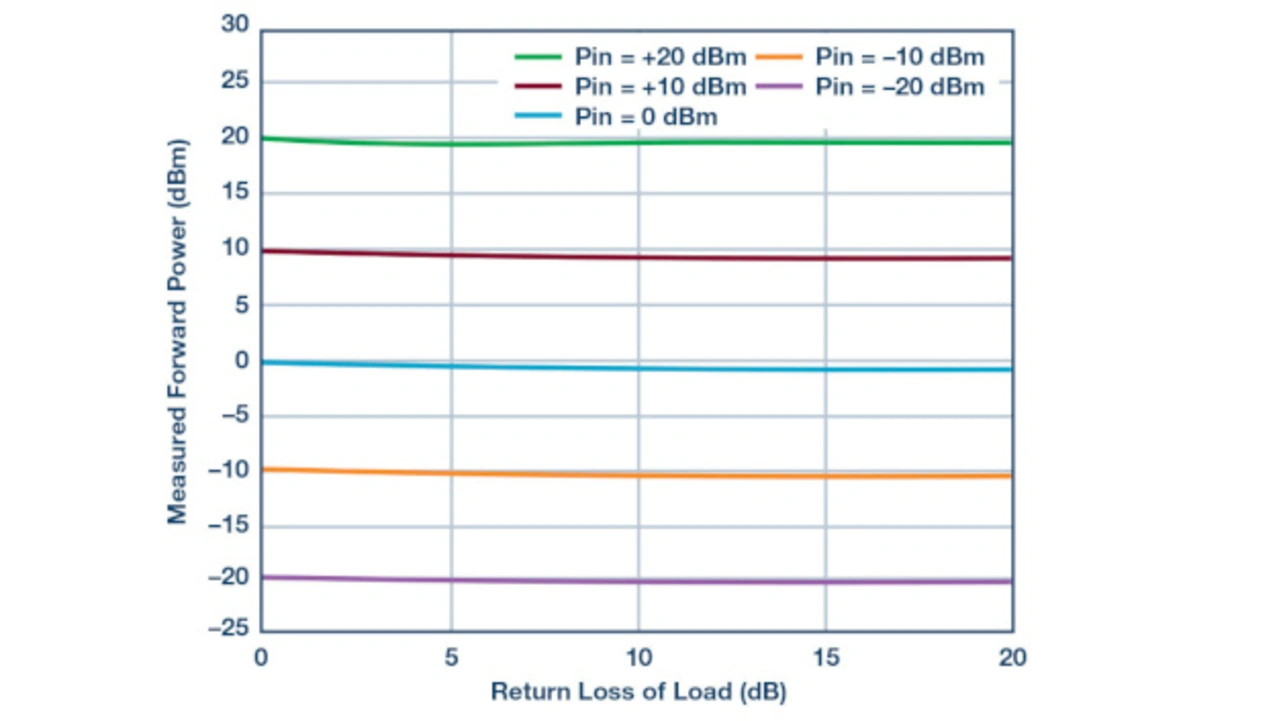
Bild 13 zeigt die Auswirkung auf die Messung der Vorwärtsleistung bei Laständerung. Definierte Leistungspegel werden an den Eingang RFIN angelegt und die Einfügungsdämpfung der Last an RFOUT zwischen 0 dB und 20 dB variiert. Wenn die Einfügungsdämpfung im Bereich zwischen 10 dB und 20 dB liegt, ist die Genauigkeit der Leistungsmessung wie erwartet recht gut. Wird die Einfügedämpfung jedoch unter 10 dB abgesenkt, steigt der Messfehler der Leistungsmessung an. Bei einer Einfügungsdämpfung von 0 dB liegt der Messfehler immer noch im 1-dB-Bereich.
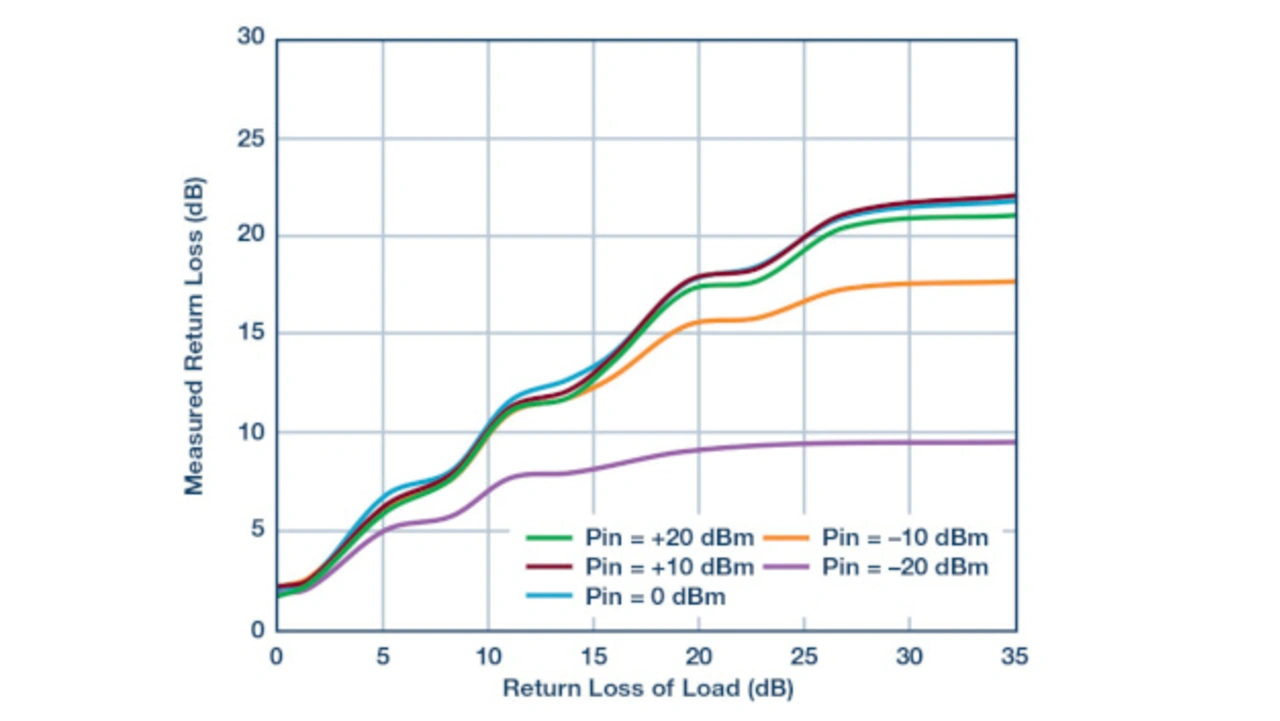
In Bild 14 misst ADL5920 die Rückflussdämpfung der Last bei 1 GHz. Dazu wird eine bekannte Rückflussdämpfung an den Port RFOUT gelegt, VFRMS und VRRMS vermessen und die Rückflussdämpfung daraus berechnet.
Der Plot birgt einige Informationen: zunächst nimmt die Genauigkeit der Messung mit höherer Rückflussdämpfung ab. Dies liegt an der Richtcharakteristik des Bausteins. Ebenso sinkt die Messgenauigkeit mit fallender Eingangsleistung. Ursache ist der begrenzte Erfassungsbereich und die Empfindlichkeit der integrierten RMS-Detektoren.
Weiterhin besitzen die Kurven eine erkennbare Welligkeit: jede Messung wird bei einer bestimmten Phasenlage der Rückflussdämpfung durchgeführt. Unter Variation der möglichen Phase ergibt sich eine Kurvenschar, deren vertikale Weite eben diese Welligkeit abbildet.
- HF-Leistung und Rückflussdämpfung bestimmen!
- Analogie als Brücke
- Lastabschluss als Störstelle
- Der Signalpfad
- Applikationen
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Emissions-Kontroll-Sensoren von Sensata
Drucksensoren verhindern schädliche Motoremissionen
Analog Devices
µModule erleichtert Kühlungsanforderungen
Forum Medizintechnik
Die Halbleitertechnik hat die zelluläre Schnittstelle erreicht
IEEE ehrt IC-Entwickler
Dr. Katsu Nakamura von Analog Devices ausgezeichnet
Sensorik und Messtechnik 2019
»Die Branche wächst und wächst und wächst«
DSP-basierte Messkarten
Industrietauglich und frei programmierbar
