Startseite > Messen + Testen > Sensorik > HF-Leistung und Rückflussdämpfung bestimmen!

Integrierte bidirektionale Messbrücke

HF-Leistung und Rückflussdämpfung bestimmen!

15. Februar 2019, 12:00 Uhr | Eamon Nash und Eberhard Brunner, Analog Devices

▶ Diesen Artikel anhören

Fortsetzung des Artikels von Teil 1

Analogie als Brücke

Wheatstone-Brücke

Der Begriff einer gerichteten Brücke geht auf die Wheatstone-Brücke (Bild 5) zurück: unter Abgleich wird dort keine differenzielle Spannung erzeugt. Die Wheatstone-Brücke hält einen Widerstand veränderlich (R₂), die anderen Widerstände (R₁, R₃, R_x) tragen feste Werte. Der Wert von R_x ist zunächst unbekannt und wird im Abgleich bestimmt: für R₁ = R₃ und R₂ = R_x verschwindet die Brückenspannung, V_OUT = 0 V.

Jobangebote+ passend zum Thema

Ingenieur/Elektroingenieur/Elektrotechniker als Field Application Engineer

GEYER Electronic GmbH, Planegg

Alle Jobangebote im Elektroniknet Karrierebereich anzeigen

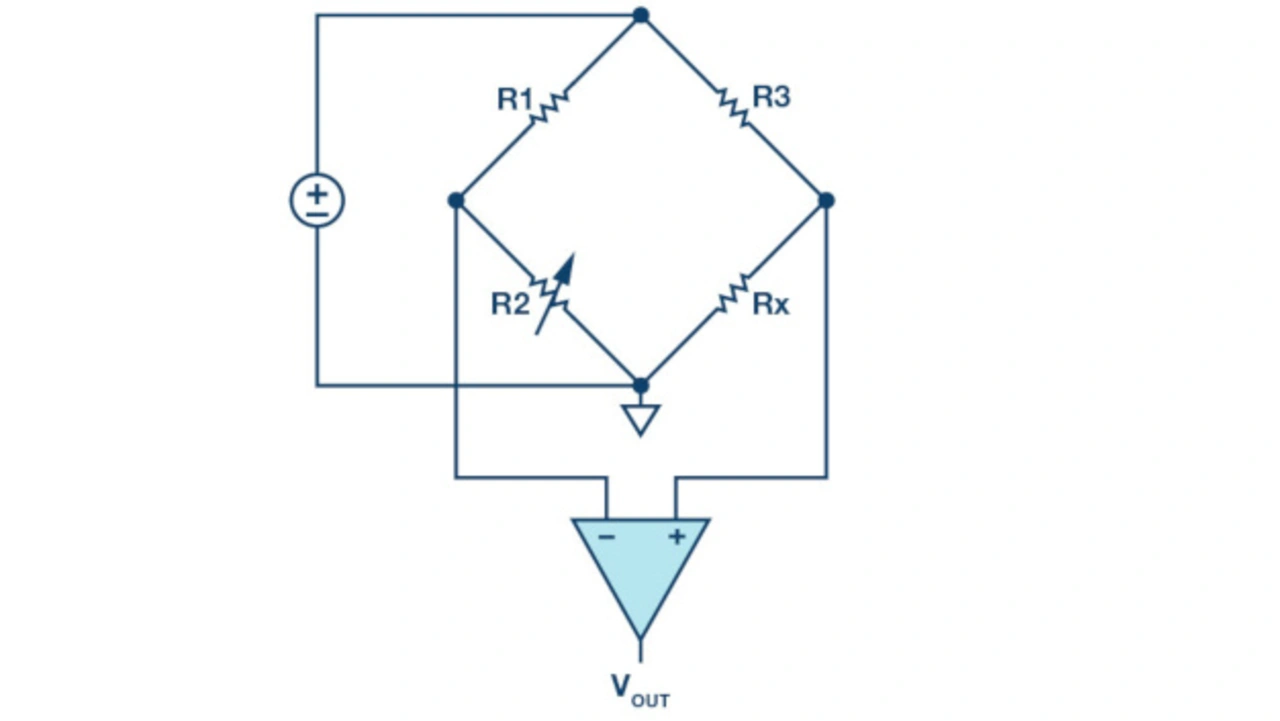
Die Brücke wird als abgeglichen betrachtet, wenn der variable Widerstand den korrekten Wert hat. Dann sind auch die Spannungsteiler-Verhältnisse der rechten und linken Brückenseite gleich.

Eine unidirektionale Brücke

Bild 6 zeigt den Schaltplan einer unidirektionalen Brücke. Dabei ist zu beachten, dass eine gerichtete Brücke immer für ein bestimmtes Z₀ entwickelt wurde und die Einfügungsdämpfung minimiert ist.

Für R_S = R_L = R = 50 Ω, wird der Messwiderstand der Brücke zu 5 Ω gewählt: das ergibt einen guten Kompromiss zwischen der Einfügungsdämpfung (< 1 dB) und der gemessenen Signalspannung. Lastseitig betrachtet resultiert R_OUT in exakt 50 Ω Portimpedanz. Die Portimpedanz R_IN errechnet sich zu 50,8 Ω (|Γ| = 0,008; RL = – 42 dB; VSWR = 1,016).

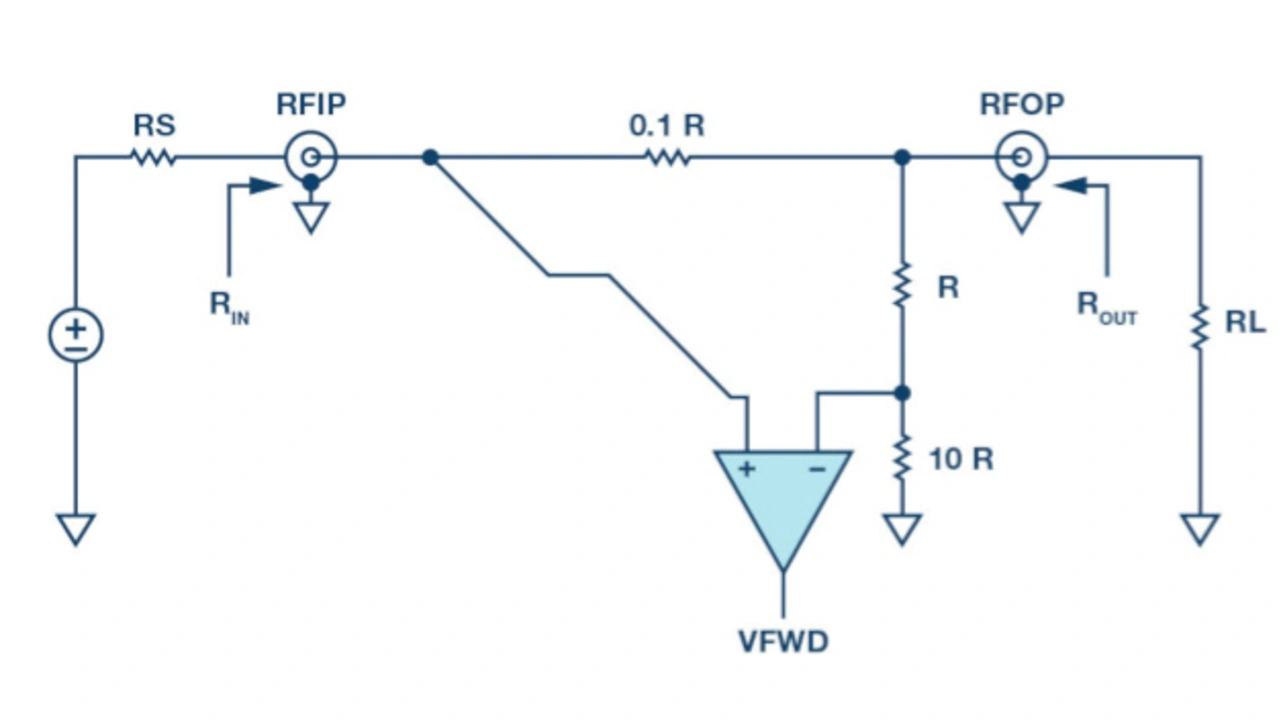
Liegt eine Eingangsleistung an RF_IP, so fällt die Spannung dort unter R_IN ~ 50 Ω nur etwa halb so hoch wie die Quellspannung aus. Bei 1 V an RF_IP resultieren rund 0,902 V an RF_OP. Diese Spannung wird vor dem negativen Eingang des Differenzverstärkers im Verhältnis 10/11 auf 0,82 V abgeschwächt, die Differenzspannung ergibt sich zu (1 - 0,82) V = 0,18 V.

Der effektive Vorwärts-Kopplungsfaktor (CPL) dieser Brücke ist:

CPL = 20 log₁₀(0,18 V / 1 V) = 15 dB	(1)

Unter idealem Abgleich sieht der V_FWD-Detektor (oder CPL-Port) keine Differenzspannung, wenn ein Signal in Rückwärtsrichtung (RF_OP > RF_IP) angelegt wird. In der Vorwärtsrichtung (RF_IP > RF_OP) ist aber die maximale Amplitude sichtbar.

Für die optimale Richtcharakteristik sind Präzisionswiderstände in dieser Topologie wichtig: integrierte Widerstände sind vorzuziehen. Zur Bestimmung der notwendigen Isolierung für die Berechnung der Rückflussdämpfung, wird das Bauteil gewendet (flip) und dann das Eingangssignal an RF_OP gelegt. Damit ist die Brücke abgeglichen: die Eingänge des Differenzverstärkers sind abgeglichen, da dieselben Teilerverhältnisse von 0,909 = (10 R) / (10 R + R) = R /( R+0,1 R) eine Differenzspannung von (V₊ - V_–) = 0 V bewirken.

Eine bidirektionale Brücke

Bild 7 zeigt einen vereinfachten Schaltplan einer bidirektionalen Brücke, ähnlich der Brücke des ADL5920. Der Widerstand für eine 50-Ω-Umgebung beträgt ebenfalls 50 Ω. Deshalb ist der Wert des Messwiderstandes der Brücke 5 Ω, während die beiden Shunt-Netzwerke jeweils rund 1,1 kΩ aufweisen.

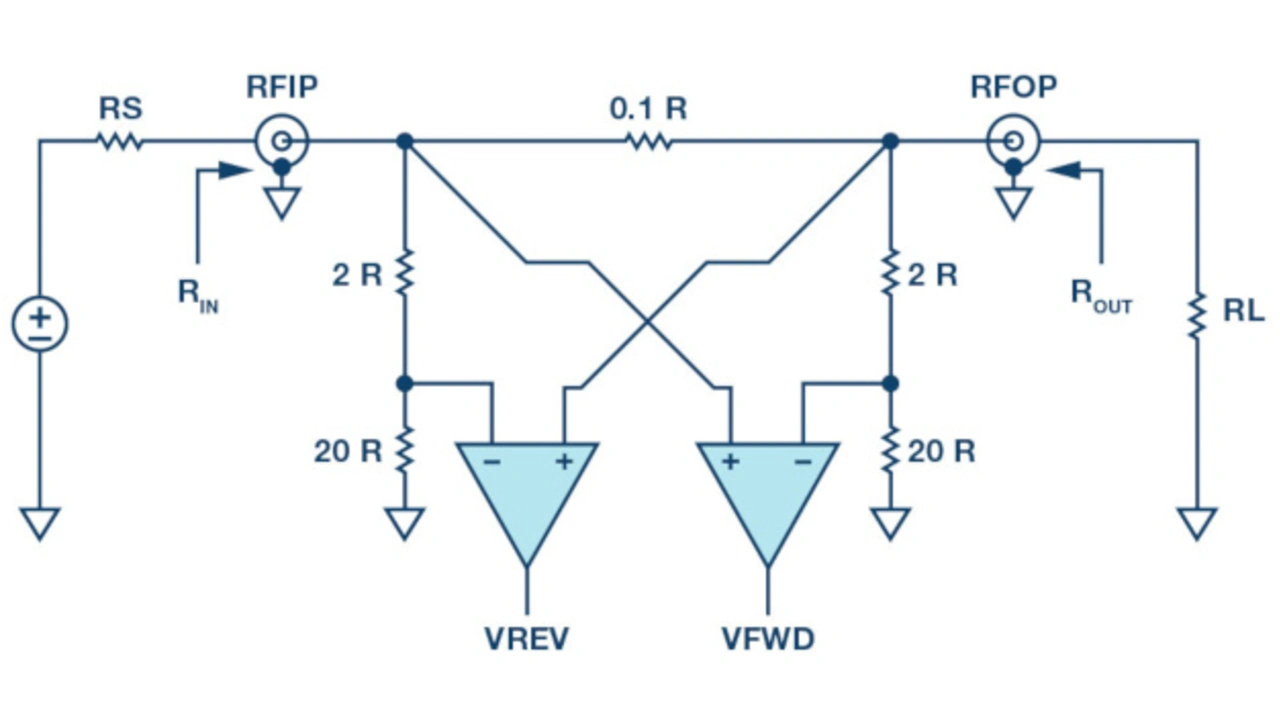
Dies ist ein symmetrisches Netzwerk: unter R_S = R_L = 50 Ω sind Ein- und Ausgangswiderstände gleich und liegen nahe 50 Ω. Wenn sowohl die Quell- als auch die Lastimpedanz 50 Ω betragen, ergibt eine ohmsche Analyse des internen Netzwerks, dass V_FWD recht groß im Vergleich zu V_REV ist. In realen Anwendungen entspricht dies einer maximalen Leistungsübertragung von der Quelle zum Verbraucher. Dies bewirkt ebenso eine geringe reflektierten Leistung und ein sehr geringes V_REV.

Dann werden Unterbrechung ( $R subscript L rightwards arrow infinity$ ) und Kurzschluss (R_L = 0) betrachtet. In beiden Fällen liefert die Ohmsche Analyse V_FWD ~ V_REV. Dies spiegelt ein reales System wider, in dem bei unterbrochener oder kurzgeschlossener Last, eingespeiste und reflektierte Leistung nahezu gleich sind.