Induktivitäten
Auswahl leicht gemacht – Spulen und Ferrite
Fortsetzung des Artikels von Teil 1
Komplexe Permeabilität
Die magnetische Eigenschaft von Materialien lässt sich über die »ma- gnetische Permeabilität« µ beschreiben. Mit µ wird eine Eigenschaft beschrieben, die die magnetische Reaktion der Flussdichte B quantifiziert, wenn das Material einer magnetischen Feldstärke H ausgesetzt ist. Die magnetische Permeabilität ist proportional zum Verhältnis der Änderungen von B und H (Gleichung 3):
Der Wert der absoluten Permeabilität µ drückt das direkte Verhältnis von B (T) zu H (A/m) aus, daher ist die resultierende SI-Einheit H/m. Die relative Permeabilität ist einheitenlos, bezieht sich auf die Permeabilität des Vakuums (µ0) und wird meist in Datenblättern von Induktivitäten angegeben. Die relativen Werte ermöglichen es, eine leicht nachvollziehbare Kennzahl zu erhalten, inwieweit das betreffende Material das Magnetfeld »besser« bündelt bzw. »konzentriert« als das Vakuum.
Somit ergibt sich der Zusammenhang nach Gleichung 4:
mit µ0 = magnetische Permeabilität des Vakuums: 1,26 × 10-6 (H/m).
Jobangebote+ passend zum Thema
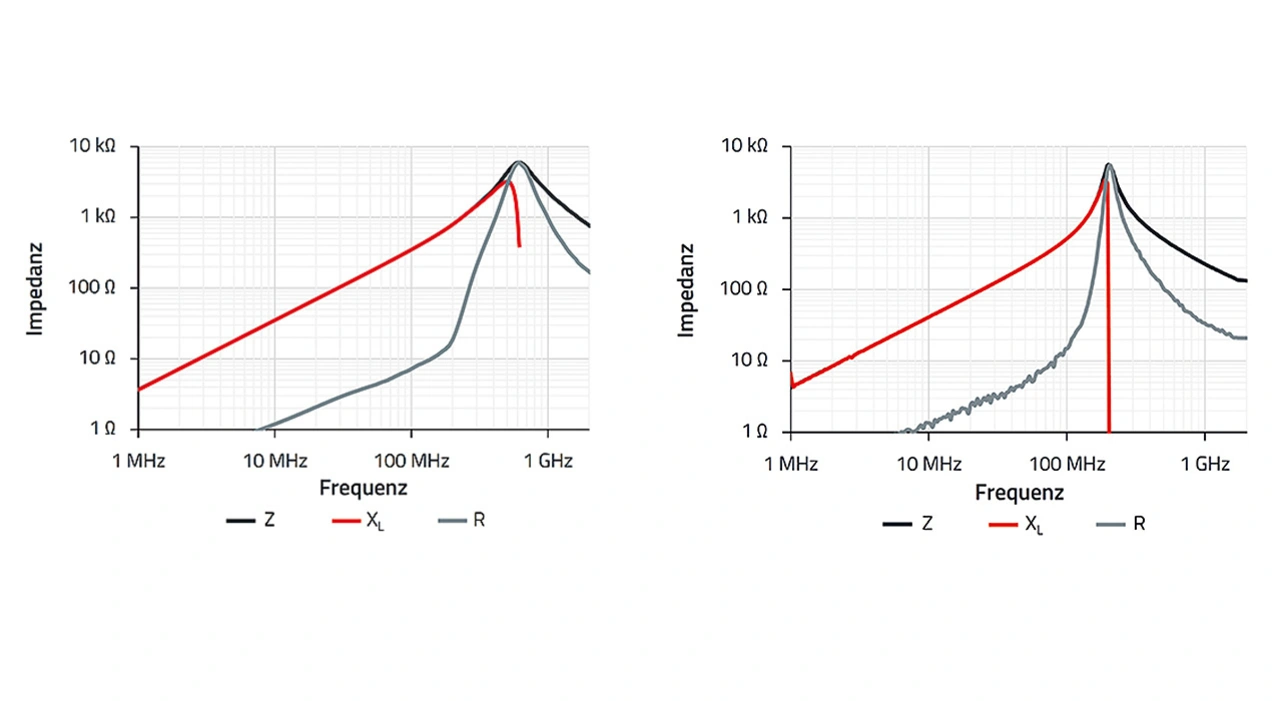
Die meisten verwendeten Ferrit-Materialien sind Eisenpulvermischungen mit Mangan-Zink(MnZn)- und Nickel-Zink(NiZn)-Beimengungen; µr liegt bei MnZn typisch im Bereich von 600 bis 15.000 und bei NiZn im Bereich von 10 bis 1.500.
Zu beachten ist, dass die relative Permeabilität stark von der Frequenz des Magnetfeldes abhängt. Weiterhin deuten die Kurven in Bild 4 schon darauf hin, dass die relative magnetische Permeabilität zwei Komponenten hat, einen realen Anteil µr‘ und einen imaginären Anteil µr‘‘.
Diese komplexe Permeabilität kommt bei hochfrequenten Magnetfeldwirkungen zum Tragen, bei denen eine Phasenverschiebung zwischen H und B entsteht. Somit ergibt sich Gleichung 5:
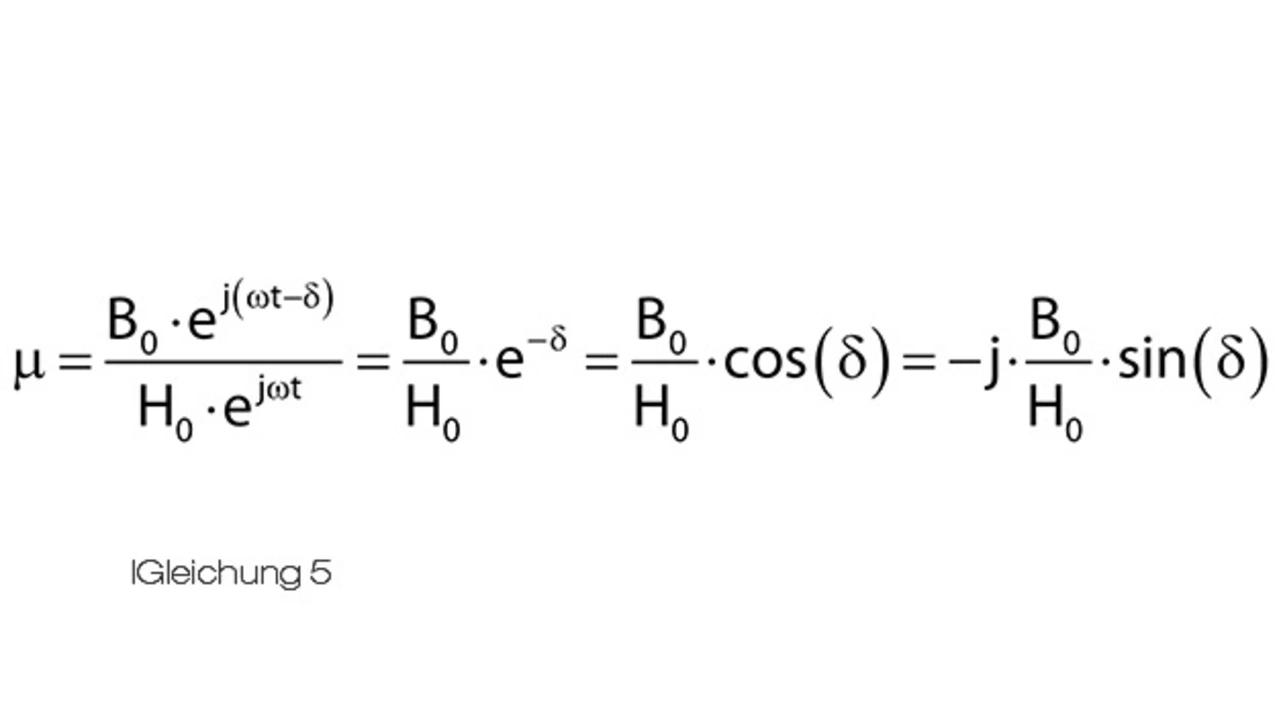
Angewendet auf die Induktivität mit Ferritkern ergeben sich die Gleichungen 6 und 7:
wobei L0 die Induktivität der Drahtwicklung ohne Ferrit ist. Somit gilt der Zusammenhang in Gleichung 8:
mit L0 = Induktivität ohne Ferrit.
Aus den Formeln lässt sich leicht erkennen, dass eine hohe Permeabilität zu einer hohen Induktivität führt, doch eine hohe Permeabilität ist meist mit höheren Kernverlusten verbunden.
Die einzelnen Komponenten der Impedanz, also Z(f), XL(f) und R(f), sind in den Datenblättern der Ferrit-Induktivitäten abgebildet. Bild 5 zeigt nun noch einmal die Impedanzkurven der Induktivität WE-RFI 744760256A.
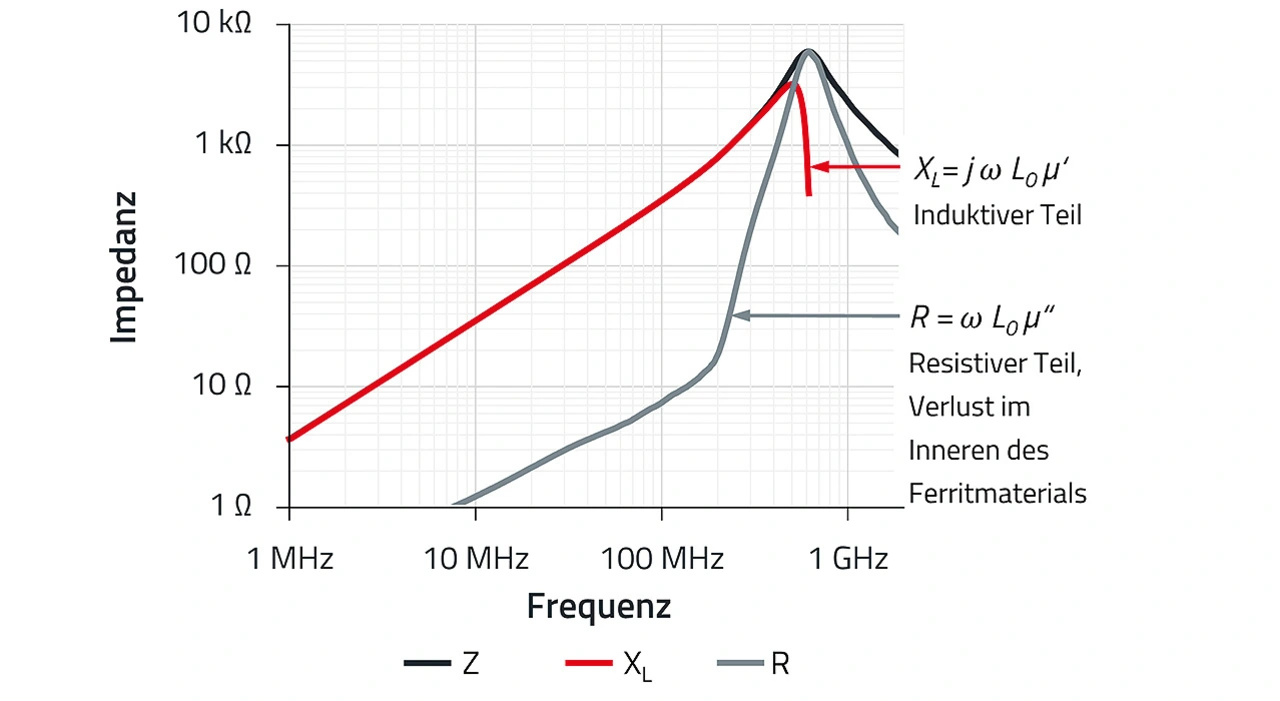
Somit wird auch klar, warum bei der Anwendung von Induktivitäten mit Ferritkern die Impedanzkurven für eine funktionierende Schaltung von hoher Bedeutung sind. Die Impedanz (Z) ist eine Vektorkombination aus Widerstand und Phase. Der Ohm’sche Widerstand R hat eine dissipative Eigenschaft, Energie wird umgewandelt und nicht zurückgewonnen. Der Blindwiderstand XL ist der Teil der Impedanz, der durch die Induktivität erzeugt wird. Die Phase ist die Verzögerung zwischen einer an das Bauteil angelegten Spannung und dem durch das Bauteil fließenden Strom. Sowohl der Ohm’sche als auch der Blindwiderstand variieren mit der Frequenz, somit also auch die Phase.
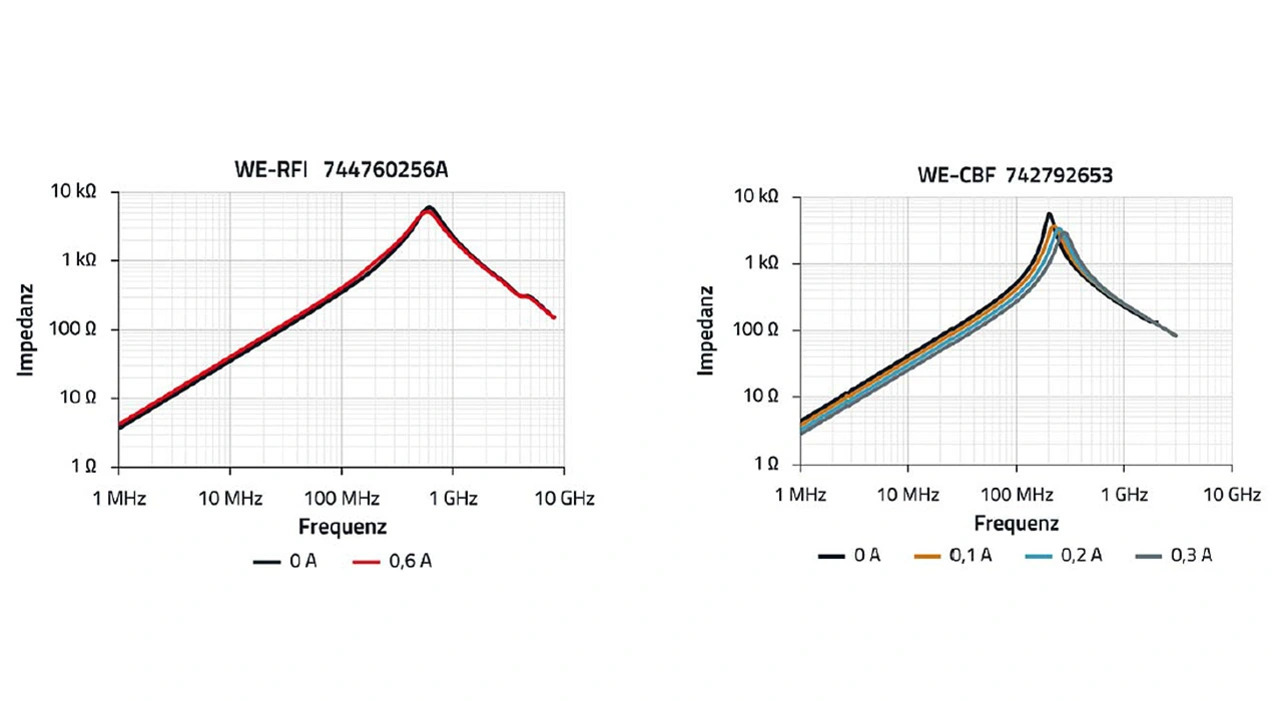
Damit aber nicht genug. Magnetische Materialien zeigen Sättigungseffekte, die über der Frequenz vor allem von der magnetischen Flussdichte, d. h. vom Strom, der durch die Ferrit-Induktivität fließt, abhängt. Man spricht hierbei von Kernsättigung, ein Effekt, den die »Luft-Induktivität« nicht hat. Bild 6 zeigt die Impedanz der beiden Induktivitäten WE-RFI 744760256A und WE-CBF 742792653 bei unterschiedlicher Gleichstrom-Vormagnetisierung (DC-Bias) über der Frequenz. Der Unterschied ist deutlich zu erkennen.
Drahtbewickelte Induktivitäten sind bei gleichem Nennstrom weniger empfindlich gegen Gleichstromvorsättigung (Current-Bias) als SMT-Ferrite.
Der Einfluss von Vormagnetisierungen unterschiedlicher Stärke auf die Impedanzkurven kann mit der Online-Simulationsplattform Redexpert [4] von Würth Elektronik für alle Artikelnummern simuliert werden.
Bevorzugte Anwendungsfelder
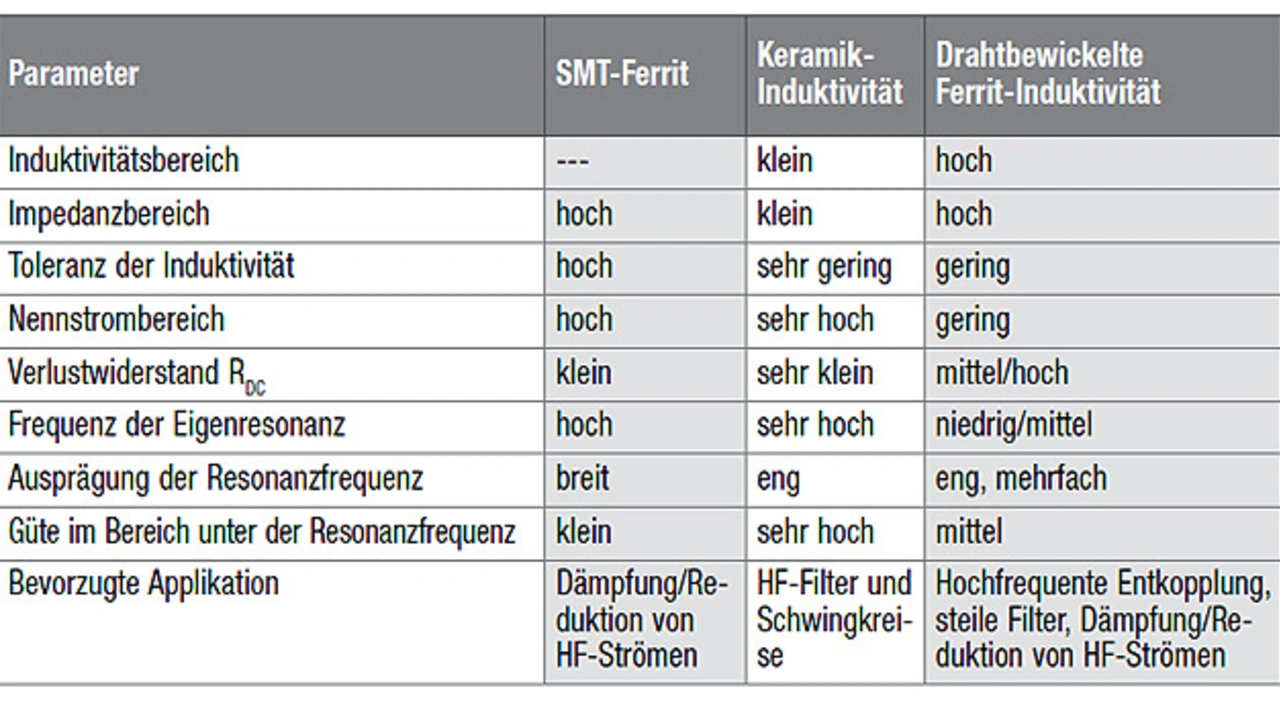
Die Tabelle gibt einen Überblick über die wichtigsten Parameter der drei Induktivitäten-Typen und ihre bevorzugten Anwendungsfelder. Die Aspekte der Messung des Impedanzverhaltens sowie detaillierte Tipps zum Einsatz der passenden Induktivität in verschiedenen Anwendungen würden an dieser Stelle den Rahmen sprengen.
Die AppNote ANP129 von Würth Elektronik, auf der dieser Artikel basiert, schlägt weiterführend einen Aufbau zur Messung des Impedanzverhaltens vor und stellt eine einfache Messmethode zur Impedanz vor. Darüber hinaus werden am Beispiel eines 20-MHz-Signalgenerators die verschiedenen Einsatzfelder der unterschiedlichen Induktivitäten-Typen dargestellt.
Literatur
[1] SMT-Ferrit WE-CBF von Würth Elektronik: https://www.we-online.com/de/components/products/WE-CBF
[2] SMT-Induktivität mit Keramikkern von Würth Elektronik: https://www.we-online.com/de/components/products/WE-KI
[3] Drahtgewickelter SMT Bead Ferrit von Würth Elektronik: https://www.we-online.com/de/components/products/WE-RFI_FERRITE_BEAD
[4] Beispiel-Simulation in RedExpert: https://we-online.com/re/5oGcZLA5
[5] Zenkner, H.: Induktivitäten, SMT-Ferrite und drahtbewickelte SMT-Ferrite – Der Draht macht den Unterschied. AppNote ANP129 von Würth Elektronik: https://www.we-online.de/ANP129
Der Autor
Dr.-Ing. Heinz Zenkner
hat Elektrotechnik mit Schwerpunkt Nachrichten- und Hochfrequenztechnik studiert und promoviert. Er ist seit vielen Jahren öffentlich bestellter und vereidigter Sachverständiger für EMV. Neben zahlreichen wissenschaftlichen Veröffentlichungen betätigt er sich häufig als Autor in vielen Werken zur EMV. Zusätzlich hat Zenkner an verschiedenen Universitäten, an der IHK und an zahlreichen Seminaren als Dozent gearbeitet. Seit vielen Jahren beschäftigt er sich mit industrieller Elektronik, von der ersten Idee eines Produktes bis hin zur Serienproduktion. Sein besonderes Interesse gilt der drahtlosen Energieübertragung, zu der er theoretisch als auch praktisch eigene Konzepte entwickelt hat.
- Auswahl leicht gemacht – Spulen und Ferrite
- Komplexe Permeabilität
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Murata treibt Miniaturisierung voran
Neues Highlight: Kleinste Chipspule der Welt
Würth Elektronik eiSos
Niedrigster Widerstand, kleinste Verluste
Thermische Modellierung
Nennstrom applikationsabhängig bestimmen
