Induktivitäten
Auswahl leicht gemacht – Spulen und Ferrite
Wie wählt man die passende Induktivität für die eigene Anwendung aus? Dafür sind unter anderem Kenntnisse über die Unterschiede von drei induktiven SMT-Bauelementen hilfreich: der Keramik-Induktivität, dem SMT-Ferrit und der drahtbewickelten Ferrit-Induktivität.
Anhand ihrer elektrischen Eigenschaften eignen sie sich für unterschiedliche Anwendungen und es lassen sich ihre physikalisch bedingten parasitären Eigenschaften sogar schaltungstechnisch als Vorteil nutzen. Induktive Bauelemente gibt es in zahlreichen Erscheinungsformen. Sehr populär sind SMT-Versionen, lassen sie sich doch einfach auf Platinen bestücken. Doch Induktivität ist nicht gleich Induktivität, wie dieser Artikel anhand von drei Vertretern von SMT-Induktivitäten demonstriert: Keramik-Induktivität, SMT-Ferrit und drahtbewickelte Ferrit-Induktivität.
Jobangebote+ passend zum Thema
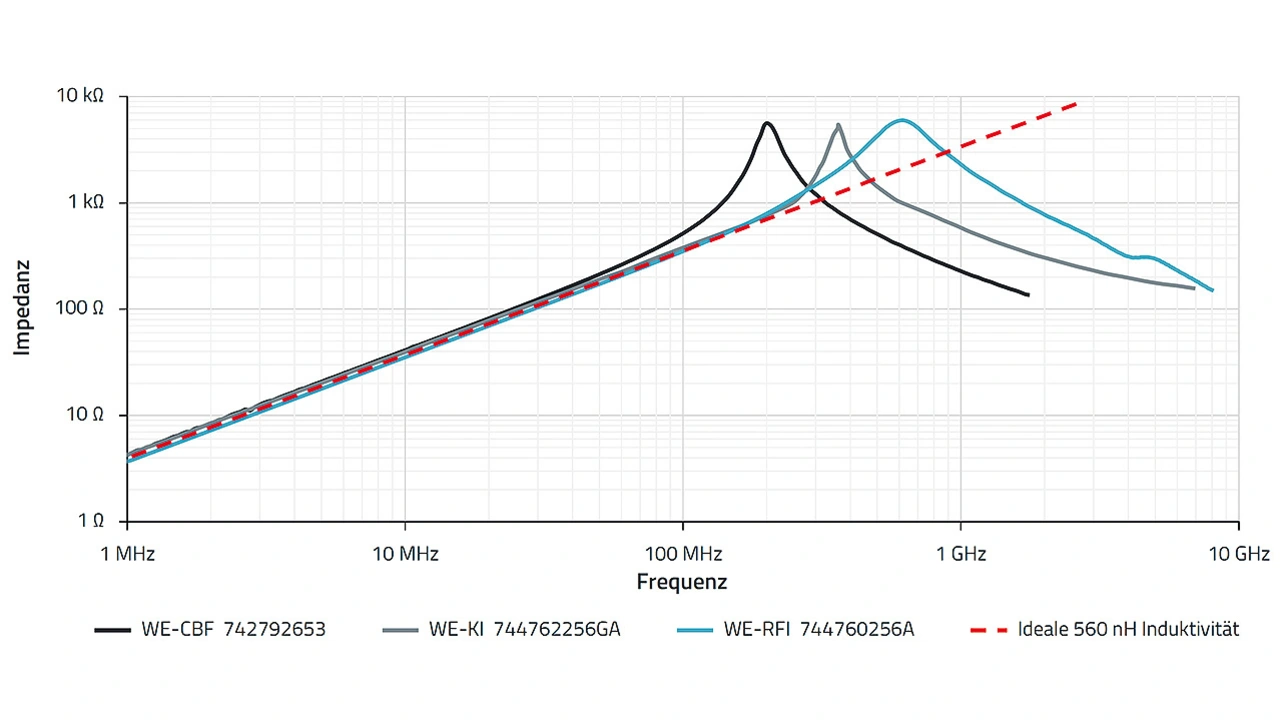
Bild 1 zeigt die Impedanzkurven der drei Induktivitäts-Typen im Vergleich:
➔ SMT-Ferrit: WE-CBF [1]
➔ SMT-Induktivität mit Keramikkern (»Luftspule«): WE-KI [2]
➔ Drahtwindungen auf Ferritkern (»drahtbewickelter Ferrit«): WE-RFI [3]
Die Komponenten wurden so gewählt, dass sie im Bereich unter ihren Impedanzmaxima einen ähnlichen Impedanzverlauf aufweisen. Die Unterschiede der Impedanzen zeigen sich im Bereich der Maxima; der SMT-Ferrit hat sein Maximum bei der niedrigsten Frequenz, der drahtbewickelte Ferrit bei der höchsten. Die Keramik-Induktivität hat im Bereich des Impedanzmaximums den steilsten Anstieg und Abfall und somit die höchste Güte Q.
Elektrische Parameter im Vergleich
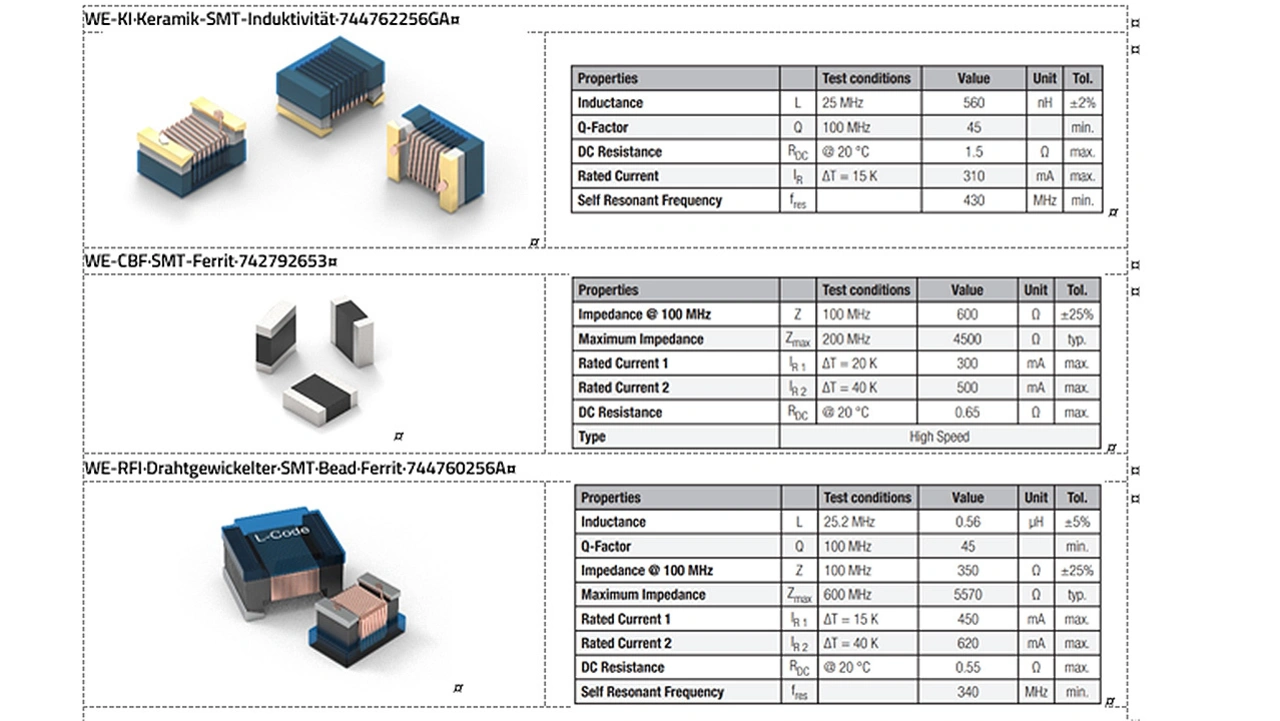
In Bild 2 sind die elektrischen Parameter der Induktivitäten gegenübergestellt. Bei Induktivitäten ohne Ferritkern (WE-KI) wird in Datenblättern die Induktivität als Wert angegeben, hier 560 nH. Der Induktivitätswert ist zwar auf eine Messfrequenz bezogen, jedoch ist der Wert unterhalb der Resonanzfrequenz über die Frequenz nahezu konstant (siehe Datenblatt).
Genau betrachtet ist der Blindwiderstand der Induktivität nicht ganz linear ansteigend mit der Frequenz. Es gibt zwei Effekte, die die Impedanz der Luftspule erhöhen: die Erhöhung des Blindwiderstandes aufgrund der Lenz´schen Regel und die Erhöhung des Widerstandes durch den Skin-Effekt.
In der rein induktiven Schaltung ist die Spule direkt an die Versorgungswechselspannung angeschlossen. Da die Spannung mit der Frequenz ansteigt und abfällt, steigt und fällt auch die selbstinduzierte gegenelektromagnetische Kraft (EMK) in der Spule in Abhängigkeit von dieser Änderung.
Es ist bekannt, dass diese selbstinduzierte Gegen-EMK direkt proportional zur Änderungsrate des Stroms durch die Spule ist (Lenz´sche Regel) und deshalb mit der Frequenz ansteigt. Somit steigt auch der Blindwiderstand der Induktivität mit der Frequenz; dieser Verlauf ist proportional.
Eine weitere Erhöhung der Impedanz geschieht durch den Skin-Effekt. Ein Leiter nutzt bei niedrigen Frequenzen seine gesamte Querschnittsfläche als Transportmedium für Ladungsträger. Wenn die Frequenz erhöht wird, stellt ein erhöhtes Magnetfeld in Richtung der Mitte des Leiters eine Impedanz für die Ladungsträger dar, wodurch die Stromdichte in der Mitte des Leiters abnimmt und die Stromdichte am Rande des Leiters ansteigt. Diese erhöhte Stromdichte in der Nähe des Randes des Leiters ist als Skin-Effekt bekannt. Der Effekt steigt mit der Frequenz und tritt auch bei allen anderen Induktivitäten (mit Ferritkern) auf. Die Resonanzfrequenz der Induktivität ohne Ferritkern entsteht primär durch die parasitäre Kapazität zwischen den einzelnen Windungen. Wann immer zwei Leiter in unmittelbarer Nähe angeordnet, aber durch ein Dielektrikum getrennt sind, und eine Spannungsdifferenz zwischen beiden existiert, bildet sich ein Kondensator.
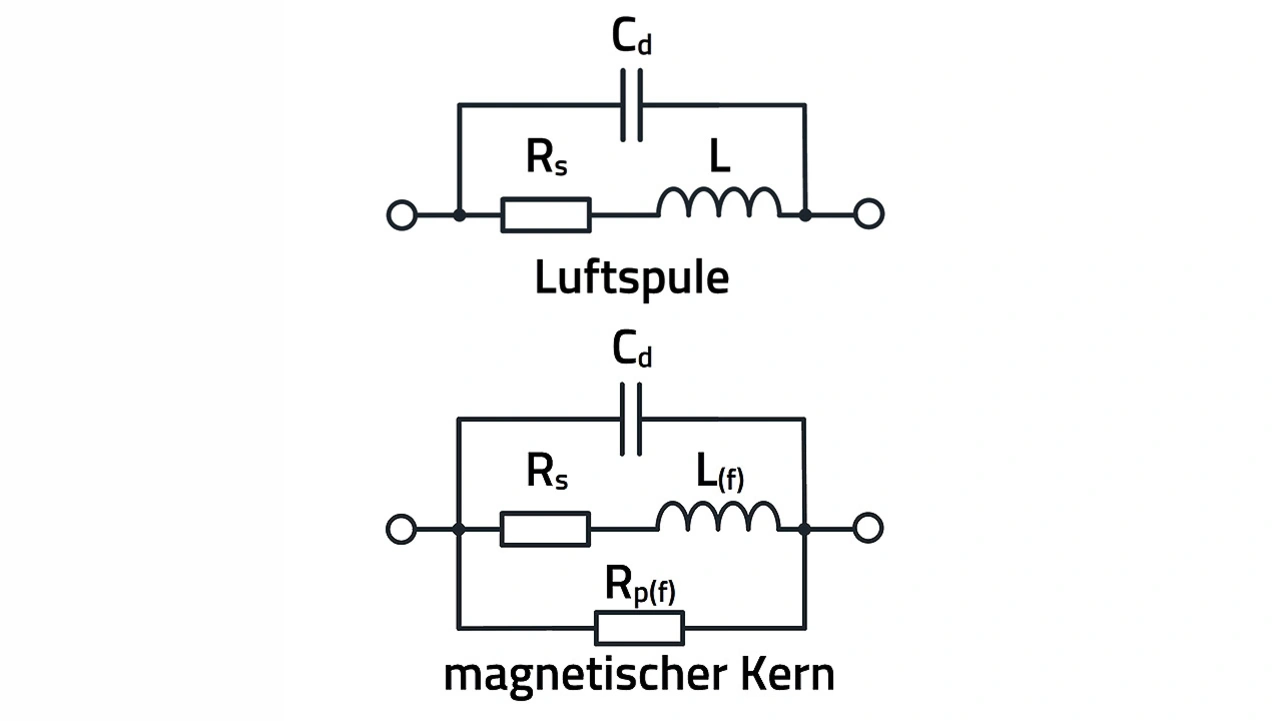
Die Kette dieser Windungskapazitäten ist parallel zu der Wicklungsinduktivität geschaltet und bildet so einen Parallelresonanzkreis. Zusätzlich ergibt sich eine parasitäre Kapazität zwischen den Anschlüssen (Lötpads), die parallel zur Windungskapazität liegt. Somit erhält man insgesamt als Ersatzschaltung eine parasitäre, der Wicklung parallel liegende Gesamtkapazität. Die äquivalente Ersatzschaltung ist in Bild 3 (oben) dargestellt.
Bei Induktivitäten mit Ferritkern (WE-RFI) und bei SMT- Ferriten (WE-CBF) ist im Datenblatt nicht ein Induktivitätswert, sondern eine Impedanz bei einer Messfrequenz angegeben. Es zeigt sich auch, dass der SMT-Ferrit die höchste Toleranz hat; die Induktivität ohne Ferrit hat die geringste Toleranz.
Da die Induktivität WE-KI keinen Ferritkern hat, benötigt sie für die gleiche Impedanz mehr Drahtwindungen als die Komponenten mit Ferrit; deshalb hat die WE-KI auch den größten Drahtwiderstand RDC. Sowohl bei der WE-KI als auch bei der WE-RFI wird ein Q-Faktor, d. h. ein Gütefaktor angegeben, bei der WE-CBF hingegen nicht. Der Q-Faktor (Q) ist ein Maß für die dissipative Eigenschaft einer Induktivität. Induktivitäten mit hohem Q-Faktor haben geringe Verluste und eine schmalbandigere Impedanzkurve. Drosseln mit niedrigem Q-Faktor haben hingegen höhere Verluste und eine breitbandigere Impedanzkurve. Die Größe der maximalen Impedanz der Induktivität hängt mit dem Gütefaktor Q zusammen.
Verlustarme Induktivitäten mit hohem Q-Faktor haben ein sehr hohes Impedanzmaximum, während eine verlustbehaftete Induktivität ein niedrigeres Impedanzmaximum aufweist. Durch Änderung der Art und Weise, wie eine Spule gewickelt ist, oder der verwendeten Kernmaterialien können das Impedanzmaximum und der Frequenzbereich des Impedanzmaximums ausgerichtet werden. Doch was hat es mit dem Impedanzmaximum auf sich?
Magnetische Kernmaterialien
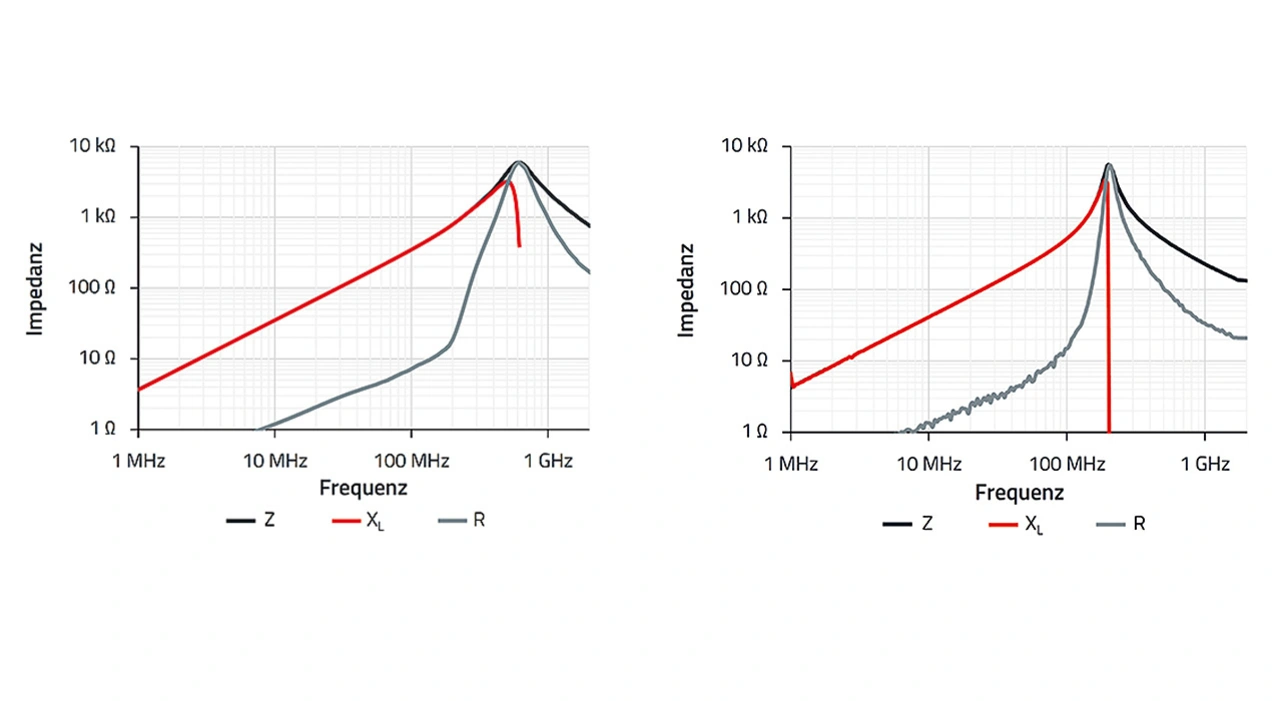
Bild 4 zeigt die Impedanzkurven über der Frequenz der Induktivität WE-RFI und des SMT-Ferrits WE-CBF. Beide Bauelemente haben Ferritmaterialien als Kernmaterial. Die Diagramme zeigen jeweils drei verschiedene Kurven: R als resistiver (ohmscher) Widerstand, XL als Blindwiderstand (induktiv) und Z als Betrag der Impedanz des Bauelements. Um Induktivitäten mit Ferritmaterial erfolgversprechend einsetzen zu können, ist das Verständnis dieser Diagramme wichtig.
In vielen Hochfrequenzanwendungen, in denen große Induktivitätswerte auf kleinem Raum benötigt werden, können Induktivitäten mit »Luftkern« aufgrund ihrer Größe nicht verwendet werden. Die Bauform der Induktivität wird kleiner, wenn der Luftkern durch ein Kernmaterial mit höherer magnetischer Permeabilität (µr > 1) ersetzt wird.
Bei gleichbleibender Größe wird der Induktivitätswert trotz verringerter Anzahl an Windungen beibehalten. Dadurch lassen sich mehrere Vorteile realisieren:
➔ Geringere Größe – aufgrund der geringeren Anzahl von Windungen, die für eine bestimmte Induktivität erforderlich sind.
➔ Erhöhte Güte – weniger Windungen bedeuten weniger Drahtwiderstand.
➔ Beeinflussung der Impedanz der Induktivität über der Frequenz – durch gezielte Auswahl/Mischung des Kernmaterials.
Die Verwendung von Magnetkernen bringt jedoch einige große Probleme mit sich, und es muss darauf geachtet werden, dass das gewählte Kernmaterial das richtige für die jeweilige Aufgabe ist; einige dieser Probleme sind:
➔ Jedes Kernmaterial ist ab einem spezifischen Frequenzbereich stark verlustbehaftet. So kann das Hinzufügen eines Magnetkerns zu einer Luftspule je nach verwendetem Material und der Betriebsfrequenz die Güte der Induktivität verringern.
➔ Die Permeabilität aller Magnetkerne ändert sich mit der Frequenz und sinkt in der Regel auf einen sehr kleinen Wert am oberen Ende ihres Betriebsbereichs. Sie nähert sich schließlich der Permeabilität von Luft (µr = 1) und wird für den Stromkreis »unsichtbar«.
➔ Je höher die Permeabilität des Kerns ist, desto empfindlicher ist er gegenüber Temperaturschwankungen. Daher kann die Induktivität der Spule über weite Temperaturbereiche erheblich schwanken.
➔ Die Permeabilität des Magnetkerns ändert sich mit dem angelegten Si- gnalpegel. Ein zu großer Strom durch die Induktivität und eine damit zu hohe magnetische Flussdichte durch den Kern führt zur Sättigung des Kerns.
Diese Probleme können überwunden werden, wenn bei der Entwicklung darauf geachtet wird, dass die Induktivitäten entsprechend ihrer Verwendung richtig ausgewählt werden; dazu benötigt man die Impedanzdiagramme mit den drei verschiedenen Impedanzkurven R, XL und Z. Der Verlauf der Kurven über der Frequenz hängt stark von den magnetischen Eigenschaften des Kernmaterials ab.
Die Ersatzschaltung einer Induktivität ohne magnetischen Kern ist in Bild 3 oben dargestellt.
Die Güte Q dieser Induktivität mit »Luftkern« ergibt sich nach Gleichung 1:
wobei für XL gilt (Gleichung 2):
mit RS = Widerstand der Wicklungen. Wenn man der Induktivität einen Magnetkern hinzufügt, sieht die Ersatzschaltung wie in Bild 3 unten aus. Es wurde der Widerstand Rp(f) hinzugefügt, um die Verluste, die im Kern selbst auftreten, darzustellen. Diese frequenzabhängigen Verluste treten in Form von magnetischer Hysterese auf. Bei der Hysterese handelt es sich um die Verlustleistung im Kern, die aufgrund der Wirbelströme und der Neuausrichtung der magnetischen Teilchen im Material bei Änderungen der Magnetisierung auftritt. Wirbelströme fließen im Kern aufgrund der darin induzierten Ströme. Zusätzlich wurde auch der Induktivität L eine Frequenzabhängigkeit L(f) zugewiesen, da wie schon oben erwähnt die magnetische Permeabilität des Materials nichtlinear über der Frequenz f ist. Somit ist die Güte einer Induktivität mit Ferritkern ein variabler Parameter, der von dem durch die Induktivität fließenden Strom und dessen Frequenz abhängt und dementsprechend individuell ermittelt werden muss.
Ferrit ist ein Material, das hauptsächlich Eisen enthält. Es wird aus einer Mischung von Eisenoxid und anderen Spurenmetallen hergestellt. Da das Material eine geringe elektrische Leitfähigkeit hat, hält es Wirbelströme und damit die Wirbelstromverluste gering. Eine besondere Eigenschaft dieser Materialien ist die starke Abhängigkeit von Frequenz, magnetischer Flussdichte und Temperatur.
- Auswahl leicht gemacht – Spulen und Ferrite
- Komplexe Permeabilität
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Murata treibt Miniaturisierung voran
Neues Highlight: Kleinste Chipspule der Welt
Würth Elektronik eiSos
Niedrigster Widerstand, kleinste Verluste
Thermische Modellierung
Nennstrom applikationsabhängig bestimmen
