Im Rauschen eingebettete Signale
Schwache Signale mit Lock-in-Verstärkern hochgenau messen
Fortsetzung des Artikels von Teil 1
Prinzip eines Lock-in-Verstärkers
Um das Signal aus Bild 1 zurückzugewinnen, könnte man einfach einen Filter mit schmalem Bandpassverlauf entwickeln, das alle Signalbestandteile bis auf die relevante Frequenz entfernt. Anschließend könnte man die Amplitude des Signals messen. In der Praxis ist die Entwicklung sehr schmaler High-Q-Bandpassfilter mit diskreten Komponenten eine sehr anspruchsvolle Aufgabe. Wenn die Spezifikationen ein sehr schmalbandiges Filter verlangen, kann es sogar unmöglich sein. Alternativ ist die synchrone Demodulation verwendbar, um das modulierte Signal auf ein Gleichstromsignal zurückzuführen, während andere Signale, die nicht auf das Referenzsignal synchronisiert sind, herausgefiltert werden. Mit dieser Technik arbeiten Lock-in-Verstärker.
Jobangebote+ passend zum Thema
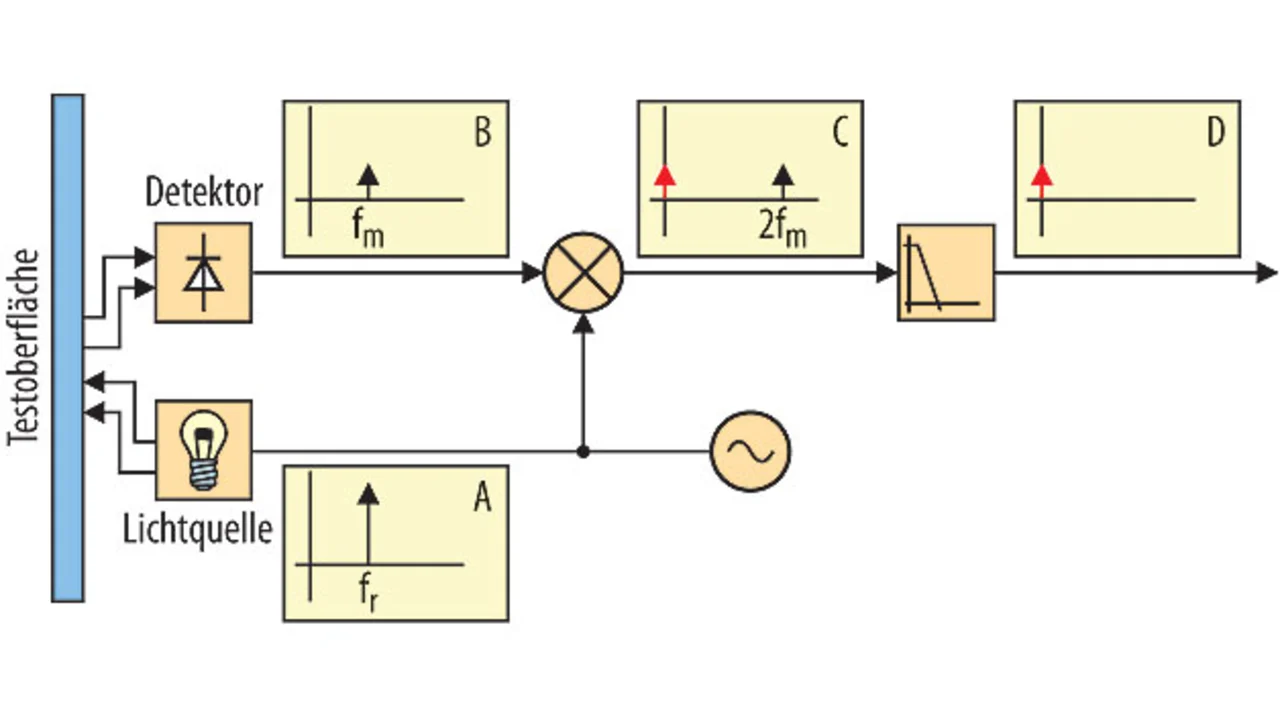
Zur Beschreibung eines Lock-in-Verstärkers kann man mit der Applikation in Bild 2 beginnen. Eine mit 1 kHz modulierte Lichtquelle beleuchtet eine Testoberfläche. Eine Fotodiode misst, wie viel Licht von der Oberfläche reflektiert wird. Die Lichtmenge ist proportional zur Menge der Verunreinigungen, die sich auf der Oberfläche angesammelt haben.
Angenommen wird, dass es sich beim Referenzsignal und bei der Messung um Sinussignale handelt (mit gleicher Frequenz und Phase, jedoch unterschiedlicher Amplitude). Außerdem wird angenommen, dass die Amplitude des Referenzsignals, das die Fotodiode treibt, fest ist und sich die Amplitude des Messsignals mit der reflektierten Lichtmenge ändert (in anderen Anwendungen würde das mit dem physikalischen Parameter, den man misst, korrespondieren).
Bei der Multiplikation von zwei Sinussignalen entsteht ein Signal mit Frequenzanteilen aus der Summe und der Differenz der beiden eingangsseitigen Sinussignale. Im hier vorliegenden Fall haben die beiden Sinussignale die gleiche Frequenz. Die Gleichung zeigt, dass sich das Ergebnis aus einem Signal mit Frequenz 0 und einem weiteren bei der doppelten Originalfrequenz zusammensetzt; das Minuszeichen bedeutet eine Phasenverschiebung um 180°. Ein Tiefpassfilter entfernt alle Bestandteile außer den DC-Anteil des Signals.
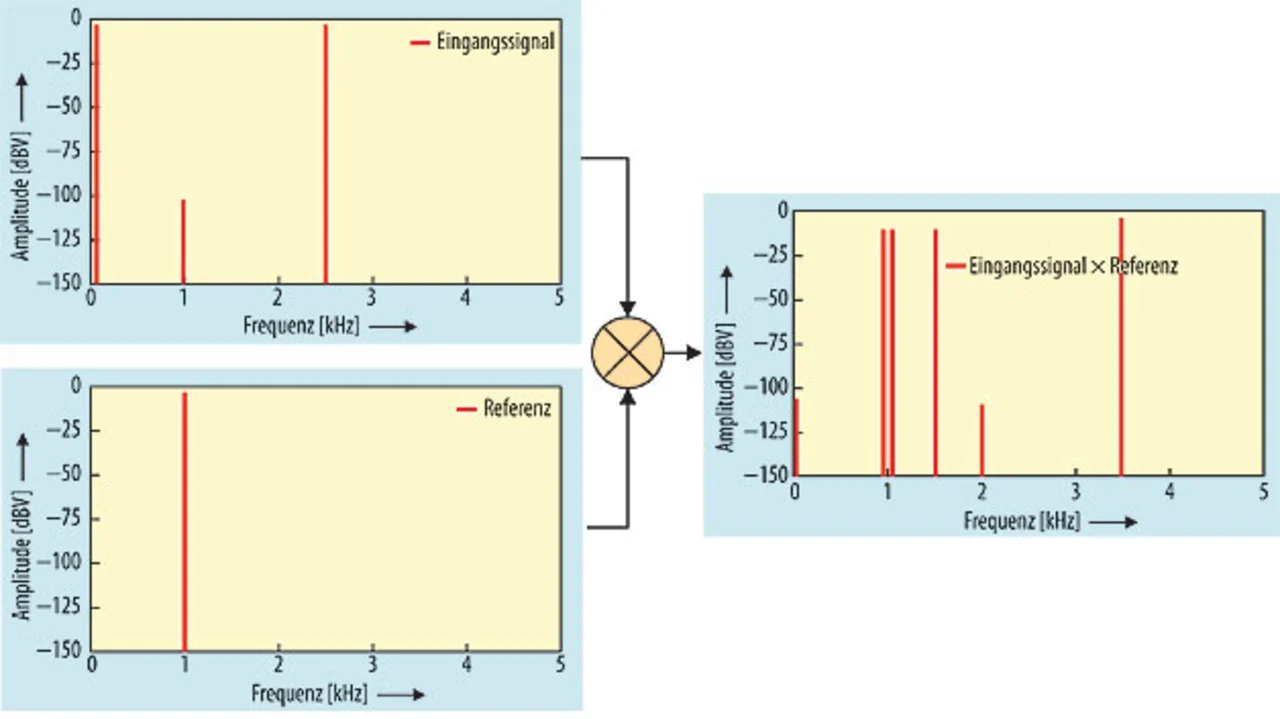
Der Vorteil beim Einsatz dieser Technik wird deutlicher, wenn man sich ein Eingangssignal mit Rauschen vorstellt. Am Ausgang der Multiplikationsstufe ist noch immer nur das Signal bei der Modulationsfrequenz in Richtung 0 Hz vorhanden. Alle anderen Frequenzkomponenten bewegen sich hin zu anderen Frequenzen. Zum Beispiel zeigt Bild 3 ein System mit starken Rauschquellen bei 50 Hz und 2,5 kHz und ein sehr schwaches Nutzsignal moduliert mit einem Sinussignal bei 1 kHz. Das Ergebnis der Multiplikation des Eingangssignals mit der Referenz ergibt ein Signal bei 0 Hz sowie andere Signale bei 950 Hz, 1,05 kHz, 1,5 kHz, 2 kHz und 3,5 kHz. Das Gleichstromsignal enthält die gewünschte Information. Somit kann man ein Tiefpassfilter nutzen, um alle anderen Frequenzen zu entfernen.
Sämtliche Rauschkomponenten, die sich in der Nähe des Nutzsignals befinden, werden bei Frequenzen nahe 0 Hz erscheinen. Daher ist es wichtig, eine Modulationsfrequenz zu wählen, die keine starken Rauschquellen bei ähnlichen Frequenzen hat. Falls dies nicht möglich ist, benötigt man ein Tiefpassfilter mit sehr niedriger Grenzfrequenz und steilem Verlauf, was allerdings auf Kosten einer langen Einschwingzeit geht.
- Schwache Signale mit Lock-in-Verstärkern hochgenau messen
- Prinzip eines Lock-in-Verstärkers
- Einfache Lock-in-Implementierungen
- Eine integrierte Alternative
- Mehrere Multipliziererstufen
- Mit FPGA und Front-End
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Analog/Digital-Wandler
Recht einfacher Treiberverstärker bringt gute Ergebnisse
Spannungsreferenzen
Genauigkeit kann man wählen
EMV von Halbleitern
ICs auf Eingangstransienten testen
Instrumentenverstärker
Offsetprobleme bei Messbrücken gelöst
Geringer Daten-Overhead
Offenes Protokoll für die einfachere, serielle Datenübertragung
Interview mit Mike Britchfield, Analog Devices
»Die Aussichten für den Analogmarkt sind aufregend«
e2v technologies
Ultraschnelle A/D-Wandler für die Wissenschaft
Zuverlässig und vernetzbar:
Halbleiterprodukte für die Industrie der Zukunft
SGMicro:
Neues Analog-Unternehmen auf dem europäischen Markt
18 Bit Auflösung
Referenzdesign für analoges I/O-Front-End in FPGA-Systemen
Analog Devices
Simulator für Linear- und Mixed-Signal-Anwendungen kombiniert Spice und Simplis
STMicroelectronics
Präzise Zero-Drift-Operationsverstärker
