HF-Digital-Analog-Umsetzer
Auswirkungen eines Baluns auf die zweite Oberwelle
Fortsetzung des Artikels von Teil 1
Erkenntnisse aus der Simulation

Ein Vergleich der Gleichungen 10 und 15 lässt erkennen, dass die HD2-Amplitude gegen Phasen-Asymmetrie empfindlicher ist als gegen Amplituden-Asymmetrie. Bei Phasen-Asymmetrie ist die zweite Oberwelle proportional zu k1, wogegen HD2 bei Amplituden-Asymmetrie proportional zur Differenz aus k1 und k2 ist. Da aber k1 und k2 nahezu gleich sind, ist die Differenz gering.
Um die Gültigkeit dieser Berechnungen zu überprüfen, wurde für das in diesem Aufsatz beschriebene Balun-Modell der in Bild 2 gezeigte Matlab-Code geschrieben. Damit lassen sich die Auswirkungen der Asymmetrie von Amplitude und Phase eines Baluns auf die Aufhebung der zweiten Oberwelle eines HF-DAUs quantifizieren und illustrieren. Das Modell enthält additives weißes Rauschen mit Normalverteilung.
Jobangebote+ passend zum Thema
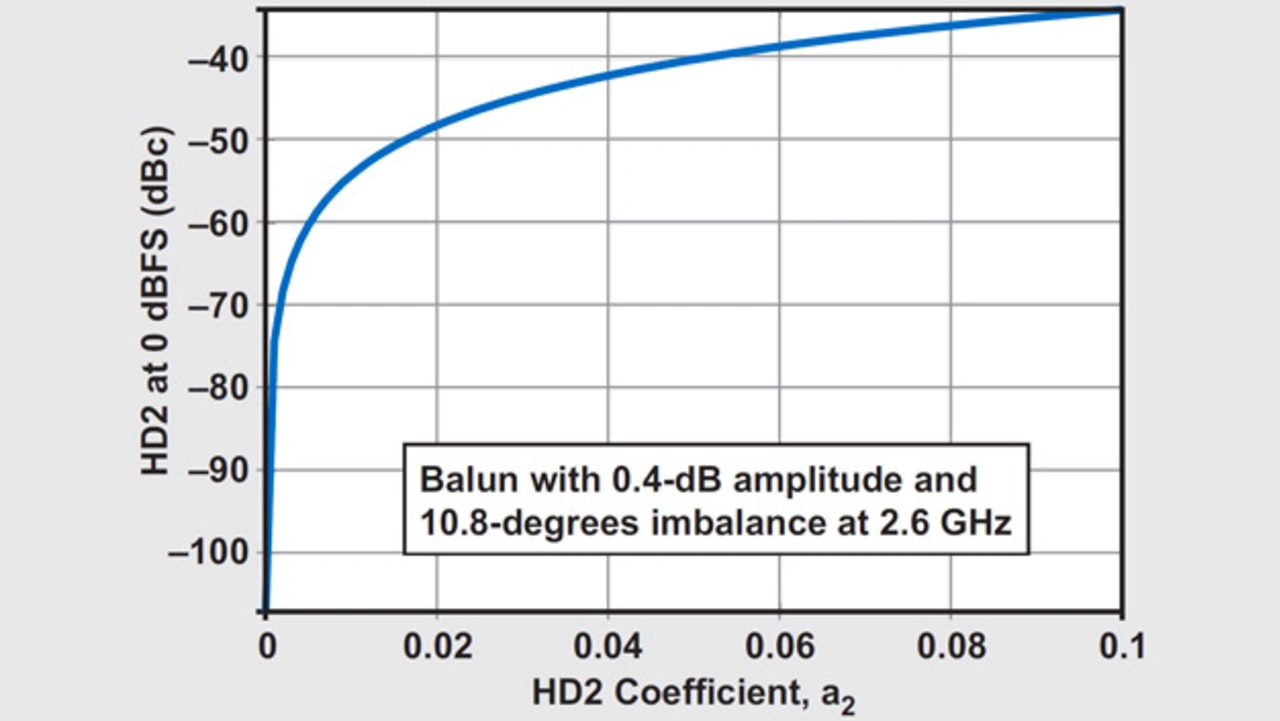
Der Verzerrungs-Koeffizient des Umsetzers (a2) bestimmt den HD2-Pegel – z.B. die Leistung oder die Amplitude. Bei einem ADU wird die HD2-Leistung normalerweise mit der Signalleistung verglichen, um eine dBc-Angabe im Frequenzbereich zu erhalten, mit der sich der HD2-Pegel ausdrücken lässt. Da der HD2-Pegel nur einen Bruchteil der Signalleistung ausmacht, liegt a2 im Bereich von 0 < a2 < 1.
Bild 3 gibt die HD2-Leistung des HF-DAUs mit einem anderen HD2-Koeffizienten a2 sowie einem Balun mit einer bestimmten Asymmetrie von Phase und Amplitude wieder. In Bild 3 beträgt die Frequenz 2,6 GHz, die Amplituden-Asymmetrie des Balun 0,4 dB und das Phasen-Asymmetrie 10,8 °. Gemäß dem Datenblatt des DAC38RF83 [1] von Texas Instruments beträgt die zweite Oberwelle 54 dBc bei einem Ausgangssignal von 0 dBFS und einer Frequenz von 2,6 GHz. Wie aus den Bildern 4a und 4b hervorgeht, hat der HD2-Koeffizient a2 des DAC38RF83 einen Wert von 0,01, a2 ist also 0,01.
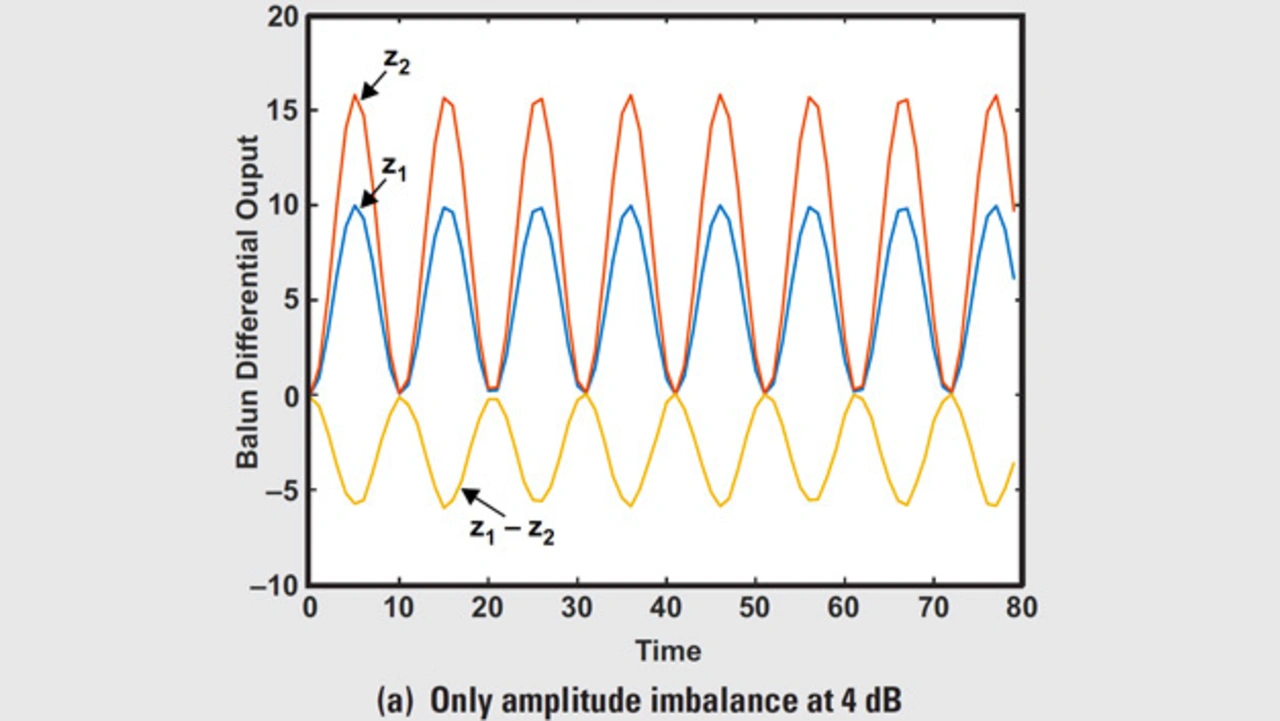
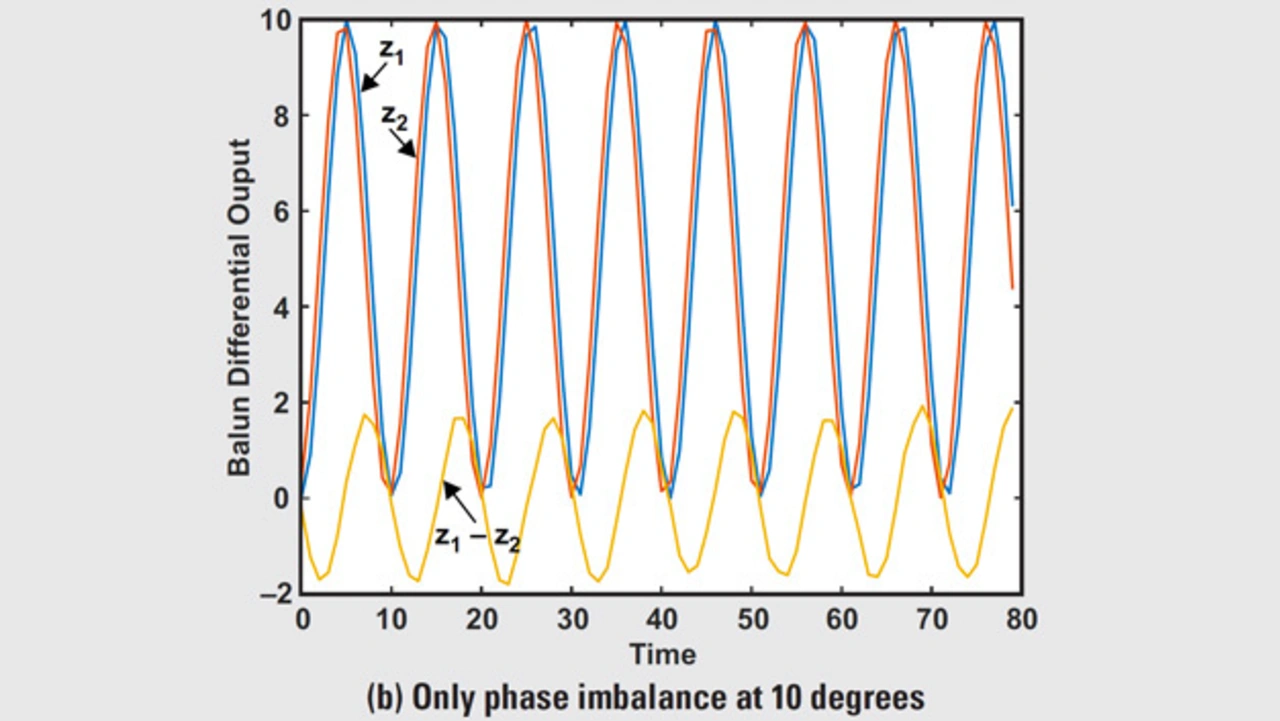
Die Bilder 4a und 4b illustrieren das Verhalten von z1(t) und z2(t) mit Asymmetrie von Phase und Amplitude. z(t) ist übrigens nicht gleich null, sodass der Balun die zweite Oberwelle des HF-DAUs nicht aufheben kann.
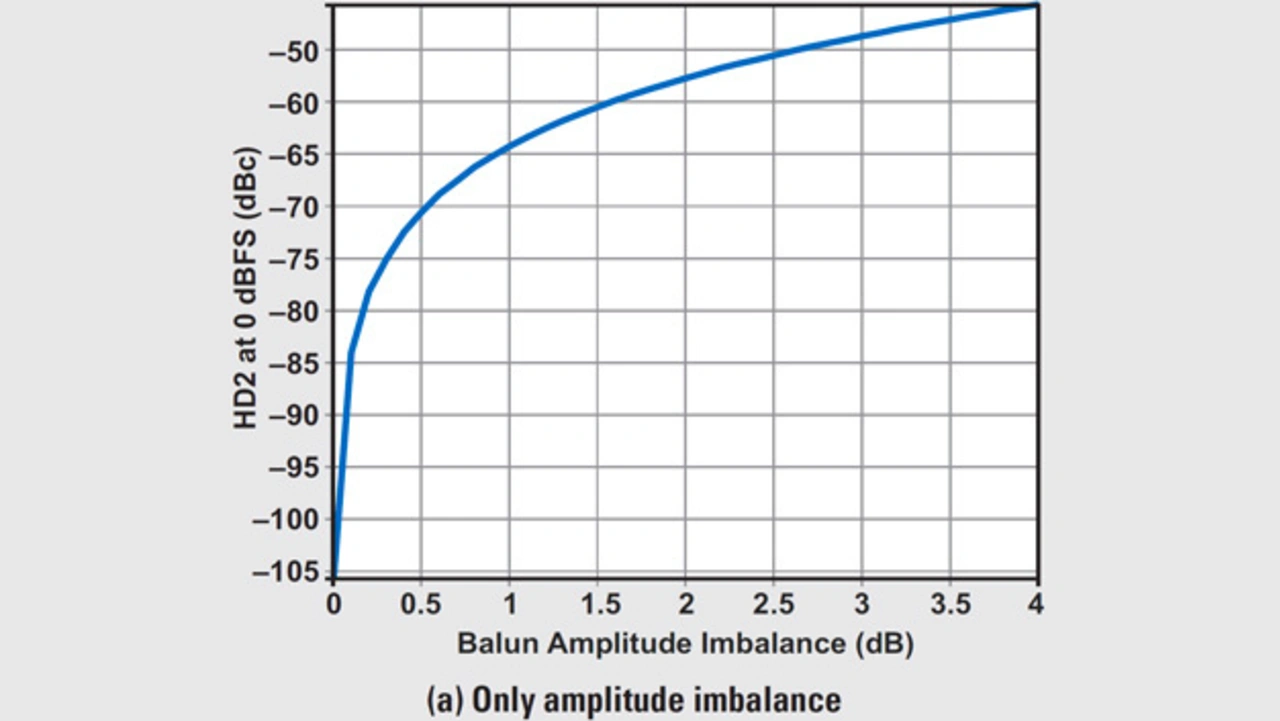
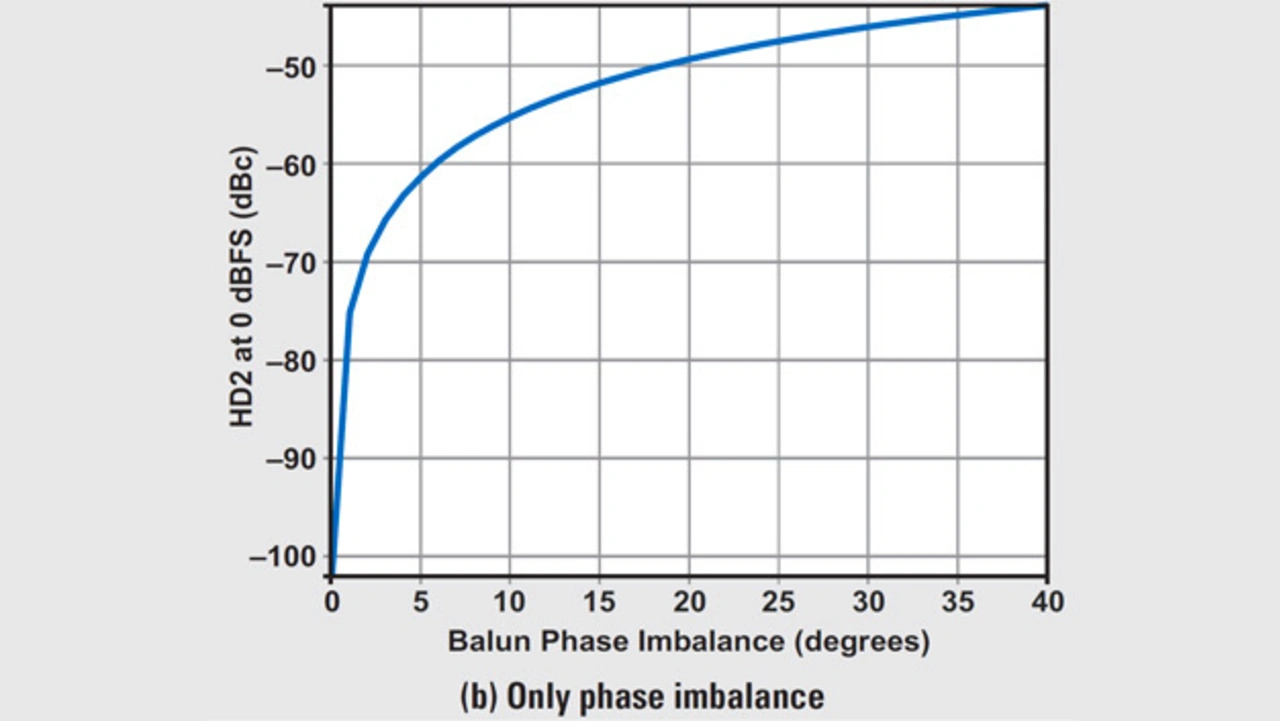
In den Bildern 5a und 5b wiederum sind die HD2-Diagramme für den HF-DAU DAC38RF83 bei 2,6 GHz dargestellt – getrennt nach Amplituden-Asymmetrie (a) und Phasen-Asymmetrie (b). Die Auswirkung unterschiedlicher Asymmetrien der Phase und Amplitude des Baluns verdeutlicht Bild 6.
Welche Asymmetrie ist kritischer?
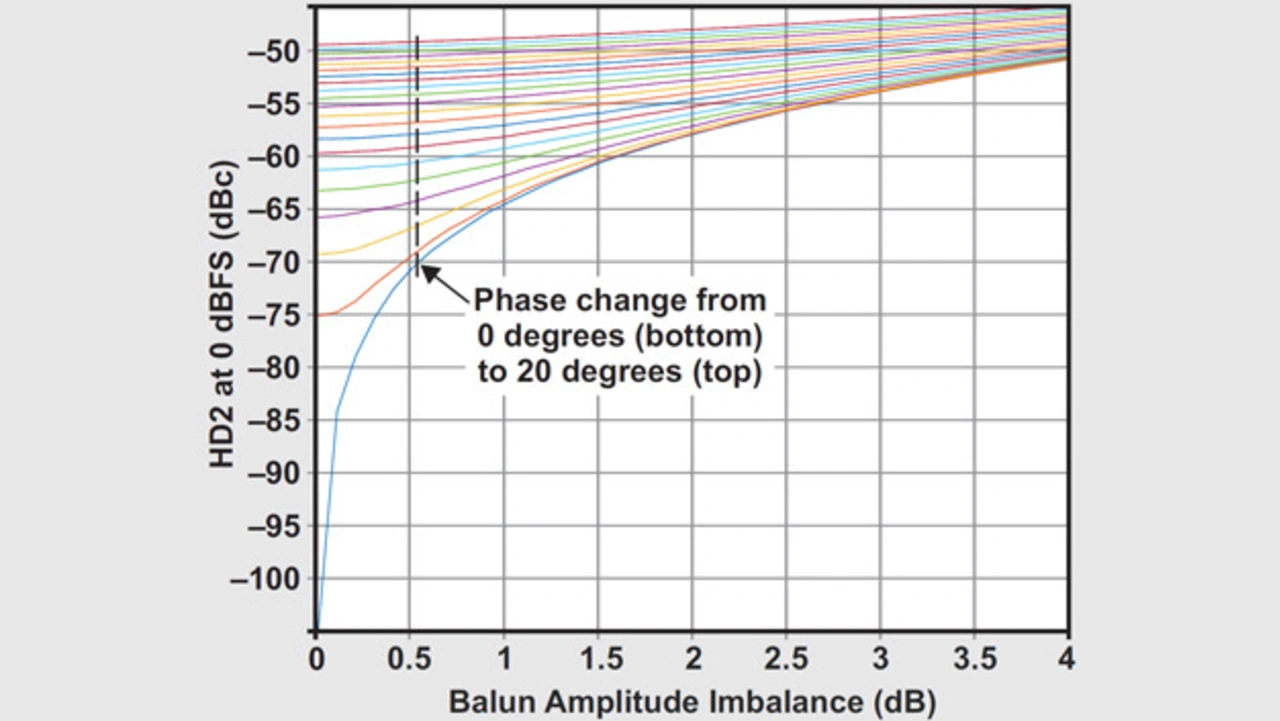
An den Gleichungen 10 und 15 wurde sichtbar, dass sich Phasen-Asymmetrie stärker auswirkt als Amplituden-Asymmetrie. Das illustrieren auch die Diagramme, die am Beispiel des HF-DAUs DAC38RF83 erstellt wurden.
Mit dem 2,6-GHz-Ausgang und dem in Bild 2 gezeigten Matlab-Code lassen sich die Auswirkungen auf das HD2-Verhalten für andere Frequenzbänder quantitativ ermitteln. Sind die quantitativen Auswirkungen bekannt, lässt sich der beste Balun ermitteln und es besteht die Möglichkeit, die Vor- und Nachteile einzelner Balun-Bauarten abzuwägen – um die optimale Leistungsfähigkeit zu erzielen.
Literatur
[1] DAC38RFxx Dual- or Single-Channel, Single-Ended or Differential Output, 14-Bit, 9-GSPS, RF-Sampling DAC With JESD204B Interface and On-Chip PLL. Texas Instruments, Datenblatt, Juli 2017, www.ti.com/lit/ds/symlink/dac38rf83.pdf.
Der Autor

Fanlong Li
ist Applikationsingenieur und leitet die Definition neuer Funk-ICs. Er hat zehn Jahre Erfahrung in der Entwicklung von Funk-ICs. Derzeit ist Li Mitglied des Technology Staff bei Texas Instruments.
asktexas@ti.com
- Auswirkungen eines Baluns auf die zweite Oberwelle
- Erkenntnisse aus der Simulation
- Übersicht der Bilder