HF-Digital-Analog-Umsetzer
Auswirkungen eines Baluns auf die zweite Oberwelle
Bei exakter Symmetrie sorgt ein Balun dafür, dass sich die zweite Oberwelle im Ausgangsspektrum eines HF-DAUs aufhebt. Doch Baluns sind nie ideal. Je nach Bauart weisen sie eine unterschiedlich stark ausgeprägte Asymmetrie von Amplitude und Phase auf. Wie lässt sich der beste Balun auswählen?
Ein Balun (balanced-unbalanced), auch als Symmetrierglied bezeichnet, setzt differenzielle Signale (symmetrisch) in massebezogene Signale (unsymmetrisch) um. Er ist ein unerlässliches Bauelement für das Netzwerk zum Anpassen des Ausgangs von HF-Digital-Analog-Umsetzern (DAU). Zu den wichtigsten Parametern, die bei der Auswahl eines Baluns für HF-DAUs beachtet werden müssen, gehören die Einfügedämpfung, die Rückflussdämpfung und Asymmetrie von Amplitude und Phase. Die Einfügedämpfung lässt Rückschlüsse auf die Bandbreiteneigenschaften eines Baluns zu. Die Rückflussdämpfung als ein weiterer nützlicher Parameter macht es möglich, den Abschluss passend zum Verhalten des Baluns bei einer bestimmten Frequenz oder in einem bestimmten Frequenzband zu konzipieren.
Entwickler sind in der Regel mit den Auswirkungen der Einfüge- und Rückflussdämpfung auf die Leistungsfähigkeit eines HF-DAUs vertraut und wissen, wie sie das beste Bauelement auswählen. Dagegen wird die Asymmetrie von Amplitude und Phase häufig übersehen, weil ihre Auswirkungen auf die Leistungsfähigkeit eines HF-DAUs nicht immer offensichtlich sind. Zum Beispiel kann ein LTCC-Balun (Low-Temperature Co-Fired Ceramics) gegenüber einem gewickelten Balun bevorzugt werden, da ein LTCC-Balun sich durch kleine Abmessungen und einen stabilen Aufbau auszeichnet. Allerdings darf nicht übersehen werden, dass LTCC-Baluns eine sehr große Asymmetrie von Amplitude und Phase aufweisen.
Es ist wichtig zu wissen, welche quantifizierbaren Auswirkungen die Asymmetrie von Amplitude und Phase eines Baluns auf die Leistungsfähigkeit eines HF-DAUs hat, denn nur so kann eine korrekte Abwägung bezüglich der Bauart und der Leistungsfähigkeit eines Baluns für eine HF-Schaltung getroffen werden.
Jobangebote+ passend zum Thema
Theoretische Analyse
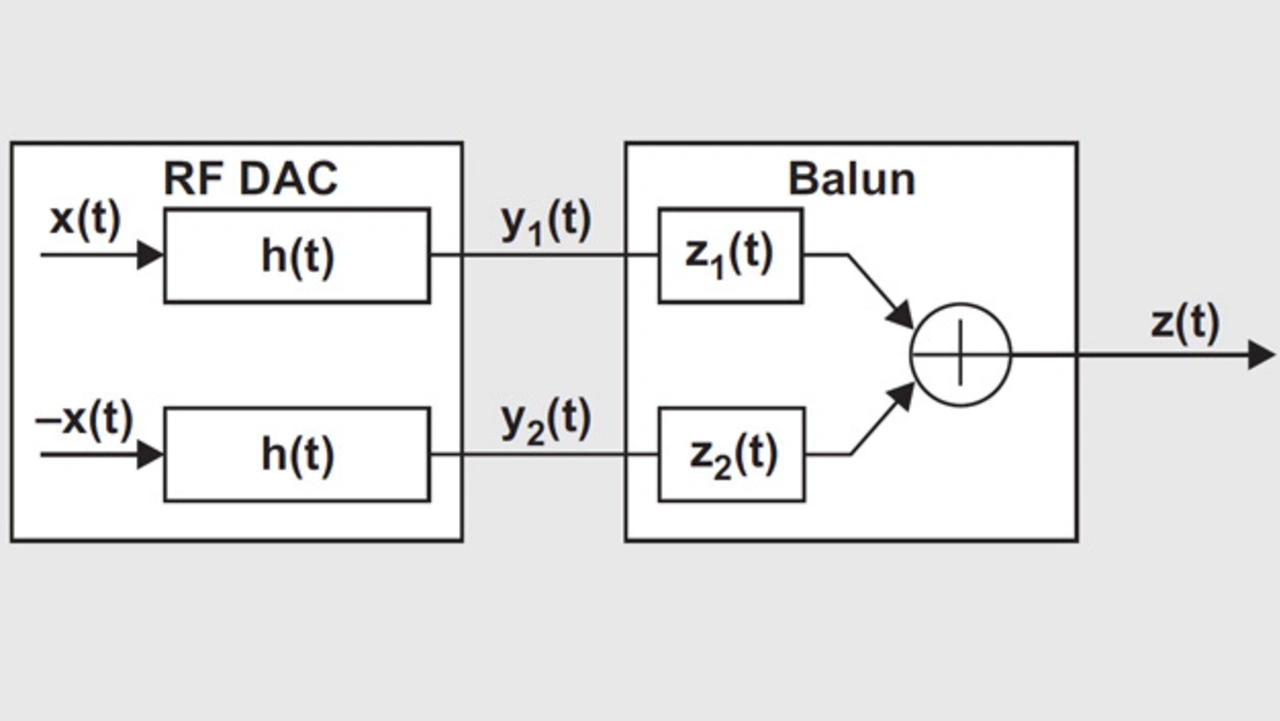
Ungeachtet einer großen Bandbreite kommt es bei der linearen Kopplung zwischen der differenziellen Primärwicklung und der massebezogenen Sekundärwicklung eines Baluns zur Asymmetrie von Amplitude und Phase. In Verbindung mit einem DA-Umsetzer oder einem anderen Bauelement mit differenziellem Ausgang sorgt die Asymmetrie für eine verschlechterte Aufhebung geradzahliger Oberwellen im Ausgangssignal des DA-Umsetzers bzw. im verarbeiteten Signal. Ist diese Asymmetrie bei niedrigen Frequenzen meist vernachlässigbar, wirken sich die zusätzlichen Verzerrungen bei sehr schnellen DA-Umsetzern sehr wohl aus. Dies gilt insbesondere für HF-DAUs.
Zunächst wird betrachtet, wie sich die Asymmetrie von Amplitude und Phase eines Baluns auf die Aufhebung der zweiten Oberwelle (2. Harmonische Störung – HD2) eines HF-DAUs auswirkt. In Bild 1 ist das Modell eines HF-DAUs mit einem externen Balun dargestellt. Ein HF-DAU verzerrt das Eingangssignal x(t) zum Ausgangssignal y(t), wobei y(t) gleichzeitig das Eingangssignal des Balun ist. Wird y(t) zur Asymmetrie von Amplitude und Phase des Balun addiert, so ergibt sich z1(t) und z2(t). Schließlich wird z1(t) plus z2(t) zum massebezogenen Ausgangssignal z(t).
Der HF-DAU lässt sich als eine symmetrische Übertragungsfunktion dritter Ordnung nachbilden. Seine Übertragungsfunktion h(t) kann somit durch Gleichung 1 ausgedrückt werden:
Das Eingangssignal x(t) wird damit nach dem HF-DAU zu y(t) und lässt sich mit Gleichung 2 ausdrücken:
Der beste Fall: Der Balun weist keine Asymmetrie auf
Weist der Balun keine Asymmetrie auf, so sind z1(t) und z2(t) vollkommen ausgewogen, d.h. sie haben die gleiche Amplitude (k1 = k2 = k) und sind zueinander um genau 180° phasenversetzt. Dies wird durch Gleichung 3 ausgedrückt.
Der Balun setzt das differenzielle Signal z1(t) und z2(t) in ein massebezogenes Signal z(t) um, das sich mit Gleichung 4 berechnen lässt.
Gleichung 4 gibt das vertraute Ergebnis für eine differenzielle Schaltung wieder: Heben sich die geradzahligen Oberwellen gegenseitig auf, ist dies bei den ungeradzahligen Oberwellen nicht der Fall.
Balun mit Amplituden-Asymmetrie
Weist der Balun eine Amplituden-Asymmetrie, aber keine Phasen-Asymmetrie auf, gilt k1 ≠ k2, was durch Gleichung 5 ausgedrückt wird.
Durch den Balun kann z(t) durch Gleichung 6 ausgedrückt werden.
Gleichung 6 lässt erkennen, dass die zweite Oberwelle (HD2) direkt proportional zur Differenz zwischen den Amplitudentermen k1 und k2 ist.
Deshalb gilt:
In einer realen Anwendung werden normalerweise sinusförmige Signale benutzt, um das HD2-Verhalten zu ermitteln. Wenn x(t) = sin (ωt), ergibt sich Gleichung 8 aus Gleichung 6.
Mit den trigonometrischen Potenzregeln:
und durch umstellen des HD2-Ergebnisses in Gleichung 8, ergibt sich Gleichung 10.
Balun mit Phasen-Asymmetrie
Erzeugt der Balun eine Phasen-Asymmetrie φ zwischen den beiden Eingangssignalen und besteht keine Amplituden-Asymmetrie, dann gilt k1 = k2 und ϕ ≠ 0. Bei einem Balun mit Phasen-Asymmetrie bestehen unterschiedliche Laufzeiten für z1(t) und z2(t). Durchläuft das Ausgangssignal des HF-DAUs also den Balun, so bewirkt dieser eine konstante Signalverzögerung mit einem entsprechenden Phasenversatz. Wenn die Phase für die Grundschwingung ϕ ist, ist sie für die zweite Oberwelle (HD2) 2ϕ und für die dritte Oberwelle (HD3) 3ϕ. Nach Durchlaufen des Balun kann ein massebezogenes Signal mit Gleichung 11 ausgedrückt werden.
In Gleichung 11 ist zu sehen, dass die Amplitude der zweiten Oberwelle proportional zum Amplitudenterm k1 ist. Deshalb gilt:
Wie erwähnt, werden sinusförmige Signale zur Ermittlung des HD2-Verhaltens eingesetzt. Wenn also x(t) = sin (ωt) ist, ergibt sich gemäß Gleichung 2 nunmehr Gleichung 13.
Werden auch hier die trigonometrischen Potenzformeln (Gleichung 9) angewendet und für 2ωt und 3ωt die Phasen 2φ und 3φ hinzugefügt, lässt sich z2(t) errechnen, wie in Gleichung 14 gezeigt.
Das massebezogene Signal z(t) ist also z1(t) + z2(t). Durch Umstellen nach 2ωt ergibt sich Gleichung 15.
Deshalb gilt:
- Auswirkungen eines Baluns auf die zweite Oberwelle
- Erkenntnisse aus der Simulation
- Übersicht der Bilder