Analogsignale digitalisieren – Teil 1
Einführung in die Rauscheigenschaften von Delta-Sigma-ADUs
Mit dieser Artikelserie werden umfassende Kenntnisse über das Rauschen in Delta-Sigma-ADUs vermittelt. Ausgehend von den gängigen Rauschquellen in einer typischen Signalverarbeitungsstufe werden Methoden gezeigt, mit denen sich das Rauschen eindämmen lässt, um präzise Digitalwerte zu erhalten.
Zu den grundlegendsten Herausforderungen beim Entwurf von Schaltungen zur Verarbeitung analoger Signale jeder Art gehört es, für ein so geringes Grundrauschen zu sorgen, dass der AD-Umsetzer (ADU) die interessierenden Signale auflösen kann. Ungeachtet jeglicher Bemühungen, die Stromaufnahme zu minimieren, die Leiterplattenfläche zu verringern oder die Kosten zu senken, wird jede Schaltung effektiv nutzlos, sobald der Rauschpegel jenen der Eingangssignale übersteigt. Es gehört deshalb zum Grundwissen eines jeden Entwicklers von analogen Schaltungen, das Rauschen in der Signalverarbeitung zu verstehen, über seine Auswirkungen auf die Analog-Digital-Umsetzung Bescheid zu wissen und Wege zu kennen, seine Auswirkungen zu minimieren.
Im folgenden wird der Begriff Genauigkeit im Zusammenhang mit dem Einfluss des Rauschens verwendet und nicht im Sinne von Exaktheit. In beiden Fällen wird der Begriff Genauigkeit häufig gleichbedeutend verwendet, auch wenn es sich um verschiedene Aspekte des Entwurfs analoger Signalverarbeitungsstufen handelt, die allerdings auch miteinander zusammenhängen. Beim Entwurf leistungsfähiger Signalerfassungssysteme muss sich der Entwickler zusätzlich zur Minimierung des Rauschens auch mit durch Ungenauigkeiten bedingten Fehlern auseinandersetzen. Beispiele sind. Nullpunkt- (Offset-) und Verstärkungs- (Skalenfaktor-)Fehler sowie die integrale Nichtlinearität (INL) und die Drift.
Jobangebote+ passend zum Thema
Was ist Rauschen und wodurch entsteht es?
Als Rauschen bezeichnet man jedes unerwünschte, meist stochastische, Signal, das neben dem gewünschten Signal vorhanden ist. Rauschen führt dazu, dass ein gewünschtes Signal von seinem ursprünglichen Wert abweicht. Es kommt prinzipbedingt in allen elektrischen Systemen vor – es gibt also keine rauschfreie Schaltung.


Bild 1 verdeutlicht, wie sich Rauschen in der Praxis äußern kann. Im linken Bild ist das Rauschen herausgefiltert, im rechten dagegen nicht. Links sind auch kleine Details erkennbar. Rechts gehen diese Einzelheiten nahezu völlig im Rauschen unter.
Bei einer Analog-Digital-Umsetzung wäre das Resultat ein Informationsverlust zwischen dem analogen Eingang und dem digitalen Ausgang, ganz ähnlich wie in Bild 1, wo kaum eine Ähnlichkeit zwischen dem linken und dem rechten Bild erkennbar ist.
In elektronischen Schaltungen tritt Rauschen in vielerlei Form auf, wie zum Beispiel:
- Breitband-, thermisches oder Johnson-Rauschen. Dieses temperaturabhängige Rauschen entsteht durch die physische Bewegung von Ladungsträgern in elektrischen Leitern.
- 1/f- oder Funkelrauschen. Die Leistungsdichte dieses niederfrequenten Rauschens ist umgekehrt proportional zur Frequenz.
- Popcorn- oder Burst-Rauschen. Dieses niederfrequente Rauschen, das durch Defekte in Bauelementen verursacht wird, ist stochastischer Natur und mathematisch nicht vorhersagbar.
Diese Arten von Rauschen können über mehrere Quellen in eine Signalverarbeitung gelangen:
- ADUs verursachen eine Kombination aus thermischem Rauschen und Quantisierungsrauschen.
- Interne oder externe Verstärker können Breitband- und 1/f-Rauschen hervorrufen, das vom ADU anschließend abgetastet wird und sich dementsprechend auf den resultierenden digitalen Ausgangswert auswirkt.
- Interne oder externe Spannungsreferenzen verursachen ebenfalls Breitband- und 1/f-Rauschen, das den digitalen Ausgangswert des ADU beeinflusst.
- Nicht-ideale Stromversorgungen können über mehrere Kopplungswege das Signal, das gemessen werden soll, durch Rauschen beeinträchtigen.
- Interne oder externe Takte erzeugen Jitter, der für eine ungleichförmige Abtastung sorgt. Dies wirkt sich bei sinusförmigen Eingangssignalen wie eine zusätzliche Rauschquelle aus und ist in der Regel umso kritischer, je schneller der ADU ist.
- Mangelhaftes Leiterplattenlayout kann dazu führen, dass Rauschen aus anderen Teilen des Systems oder aus der Umgebung in empfindliche analoge Schaltungen gekoppelt wird.
- Sensoren können in hochauflösenden Systemen zu den Bauteilen mit dem stärksten Rauschen gehören.
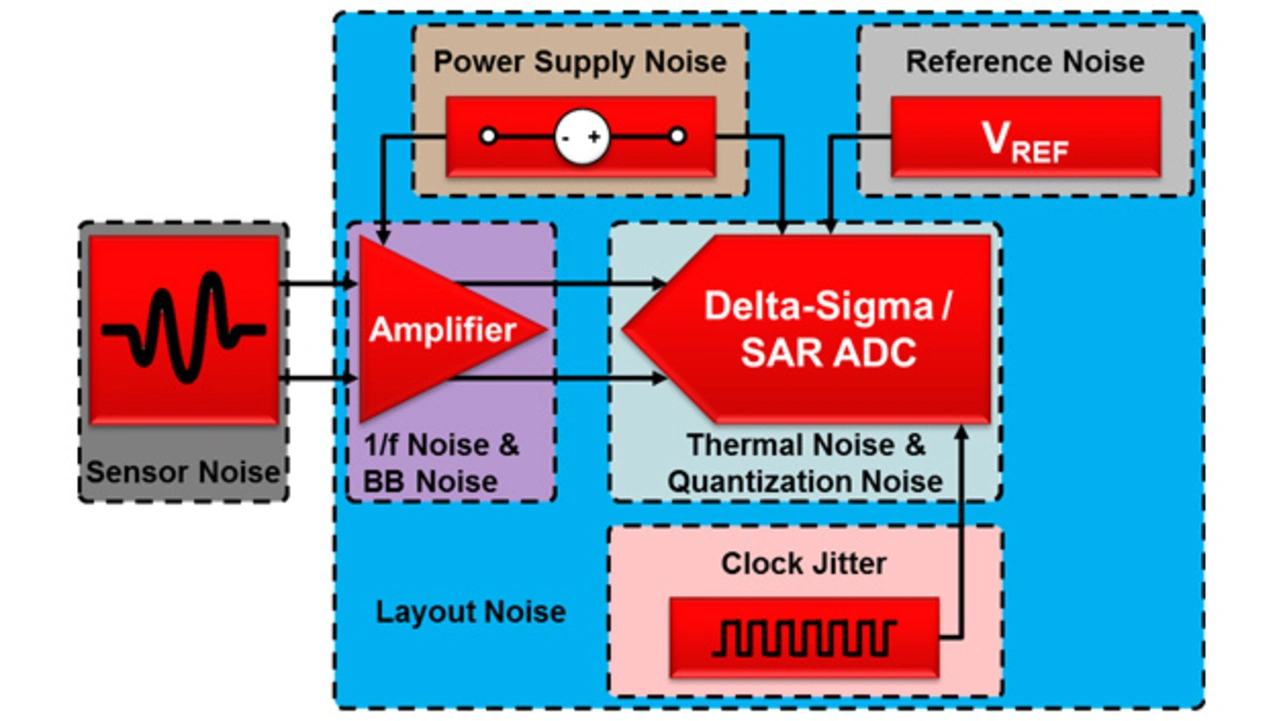
Bild 2 zeigt diese Rauschquellen in einer typischen Schaltung mit ADU zum Verarbeiten analoger Sensorsignale.
In diesem Beitrag wird ausschließlich das systemimmanente Rauschen von ADUs behandelt.
Das systemimmanente Rauschen von ADUs
Zwei Hauptquellen sind für das gesamte Rauschen eines ADUs verantwortlich: das Quantisierungsrauschen und das thermische Rauschen. Da keine Korrelation zwischen beiden Rauschquellen besteht, lässt sich das Gesamtrauschen des ADUs (NADU, Total) nach der Root-Sum-Squares-Methode (RSS) berechnen, wie in Gleichung 1 gezeigt:
Jede Rauschquelle in einem ADU weist spezifische Eigenschaften auf, auf die es ankommt, wenn es um Möglichkeiten zur Eindämmung des systemimmanenten Rauschens eines ADUs geht.
Quantisierungsrauschen
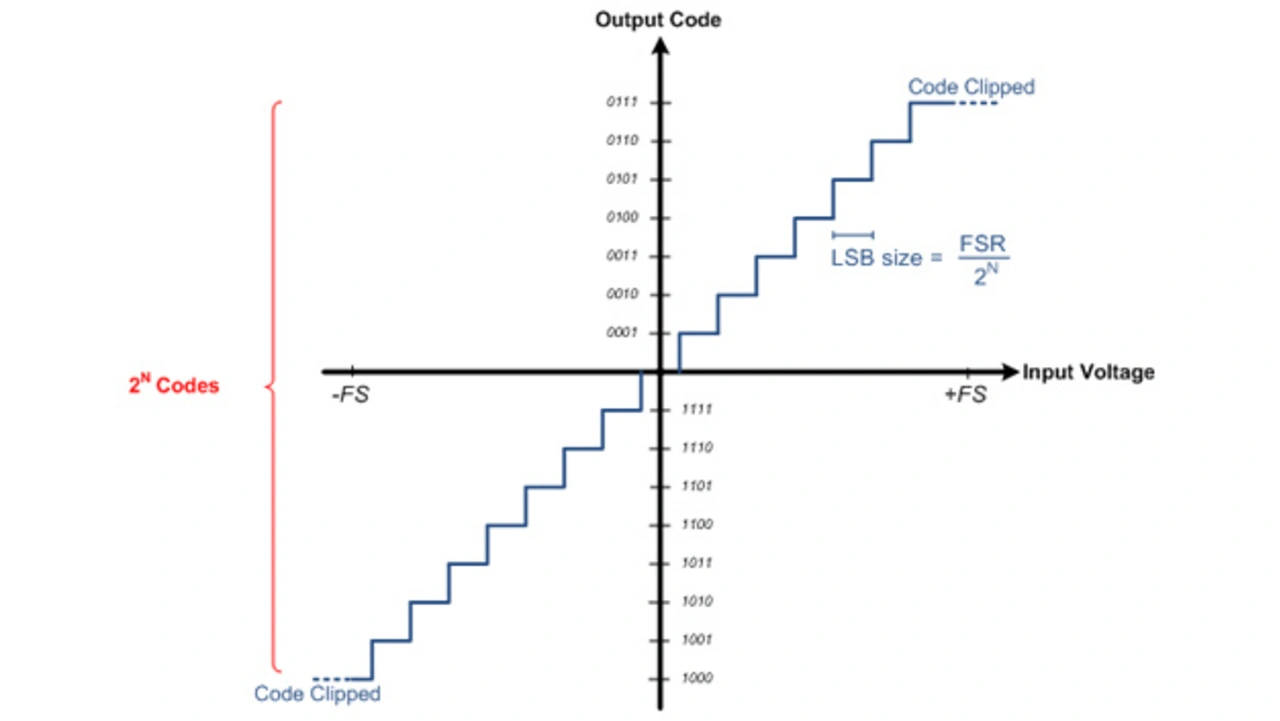
Bild 3 zeigt die ideale, d.h. von Offset- und Verstärkungsfehlern unbeeinflusste, Übertragungsfunktion eines ADUs. Sie erstreckt sich in horizontaler Richtung von der minimalen bis zur maximalen Eingangsspannung und ist in vertikaler Richtung in die maximale Zahl der ADU-Werte unterteilt. Im vorliegenden Fall gibt es 16 Werte oder Schritte, denn es handelt sich um einen 4-bit-ADU. Hinweis: Die Übertragungsfunktion eines ADUs mit direktem Binärcode befände sich ausschließlich im ersten Quadranten.
Das Quantisierungsrauschen entsteht durch die Abbildung unendlich vieler analoger Spannungen auf eine endliche Anzahl digitaler Werte. Die Folge ist, dass jeder digitale Ausgangswert für mehrere analoge Eingangsspannungen stehen kann, die sich um bis zur Hälfte des niederwertigsten Bits (Least Significant Bit, LSB) unterscheiden können. Das LSB ist gemäß Gleichung 2 definiert:
in der Gleichung steht FSR (Full Scale Range) für den Vollaussteuerungsbereich in V und N für die Auflösung des ADUs in bit.
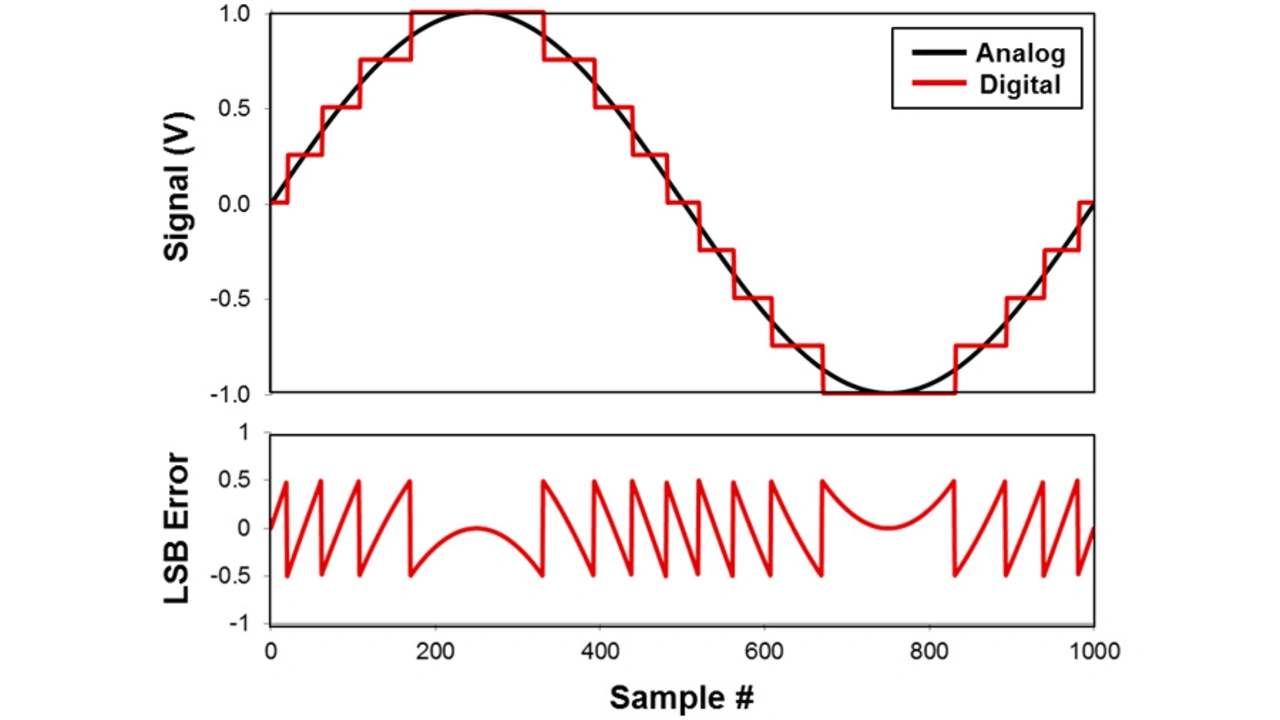
Wird die Quantisierung eines stetig variierenden Signal grafisch dargestellt, so ergibt sich ein Graph, wie er in Bild 4 zu sehen ist. Der Unterschied zwischen dem quantisierten, stufenförmigen digitalen Ausgang eines ADUs und dem gleichmäßigen, sinusförmigen analogen Eingangssignal ist sofort zu erkennen. Wird die Differenz zwischen beiden Kurven gebildet, so ergibt sich die unten in Bild 4 dargestellte sägezahnförmige Fehlerkurve. Dieser Fehler variiert um ±0,5 LSB und wirkt sich im Ergebnis als Rauschen aus.
Auf ähnliche Weise kommt es auch bei statischen Eingangssignalen zu einer Abweichung vom Eingangssignal um bis zu ±0,5 LSB. Da es jedoch bei statischen Signalen keine Frequenzkomponente gibt, äußert sich das Quantisierungs-»Rauschen« am Ausgang des ADUs als Offsetfehler.
Eine ebenso offensichtliche wie bedeutsame Auswirkung des Quantisierungsrauschens ist ferner, dass ein ADU nicht genauer messen kann, als es seine Auflösung zulässt, denn Änderungen des Eingangssignals um weniger als 1 LSB werden von ihm nicht erkannt.
Thermisches Rauschen
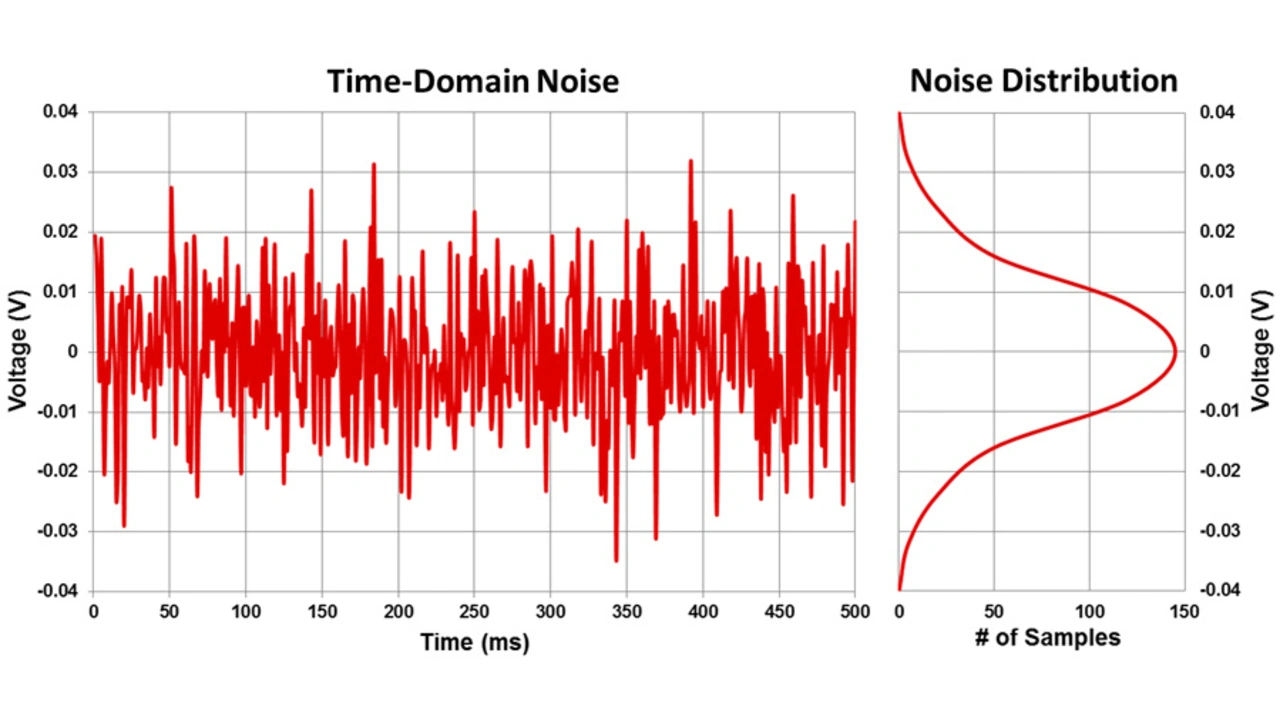
Handelt es sich beim Quantisierungsrauschen um ein Nebenprodukt der Analog-Digital-Umsetzung – oder auch Digital-Analog-Umsetzung –, so ist das thermische Rauschen ein Phänomen, das in allen elektrischen Bauteilen vorkommt. Es wird durch die physische Bewegung der Ladungsträger in elektrischen Leitern verursacht und lässt sich folglich sogar ohne Anlegen eines Eingangssignals messen.
Leider hat der Entwickler der einen ADU einsetzt keinen Einfluss auf das thermische Rauschen des Bauelements, da es durch die Konstruktion des ADU vorgegeben ist. Im weiteren Verlauf werden alle ADU-Rauschquellen, bei denen es sich nicht um das Quantisierungsrauschen handelt, als das thermische Rauschen des ADU bezeichnet.
Bild 5 stellt das thermische Rauschen im Zeitbereich dar, wobei die typische gaußsche Verteilung erkennbar ist.
Das systemimmanente thermische Rauschen eines ADUs kann nicht beeinflusst werden, aber das Quantisierungsrauschen lässt sich potenziell durchaus ändern, da es von der Größe des LSB abhängt. Um die Bedeutung dieser Änderung quantifizieren zu können, kommt es jedoch darauf an, ob ein ADU mit hoher oder niedriger Auflösung verwendet wird.
Hohe und niedrige Auflösung bei ADUs
Als niedrigauflösend werden ADUs bezeichnet, wenn ihr Gesamtrauschen vom Quantisierungsrauschen dominiert wird (NADU, Quantisierung >> NADU, Thermisch). Umgekehrt gelten ADUs als hochauflösend, wenn in ihrem Gesamtrauschen das thermische Rauschen vorherrscht (NADU, Quantisierung << NADU, Thermisch). Die Grenze zwischen beiden liegt meist bei einer Auflösung von 16 bit, sodass Wandler mit mehr als 16 bit Auflösung als hochauflösend und solche mit weniger Auflösung als niedrigauflösend bezeichnet werden. Auch wenn diese Konvention nicht in jedem Fall zutreffen mag, wird sie im folgenden durchgängig verwendet.
Weshalb aber liegt die Grenze genau bei 16 bit? Die Antwort lässt sich in zwei ADU-Datenblättern finden. Der Vergleich der Rauschtabelle des 16-bit-Delta-Sigma-ADUs ADS114S08 [1] von Texas Instruments mit der Rauschtabelle des entsprechenden ADUs mit 24 bit, nämlich des ADS124S08, verdeutlicht den Zusammenhang (Bild 6). Von ihrer Auflösung abgesehen, sind beide ADUs identisch.
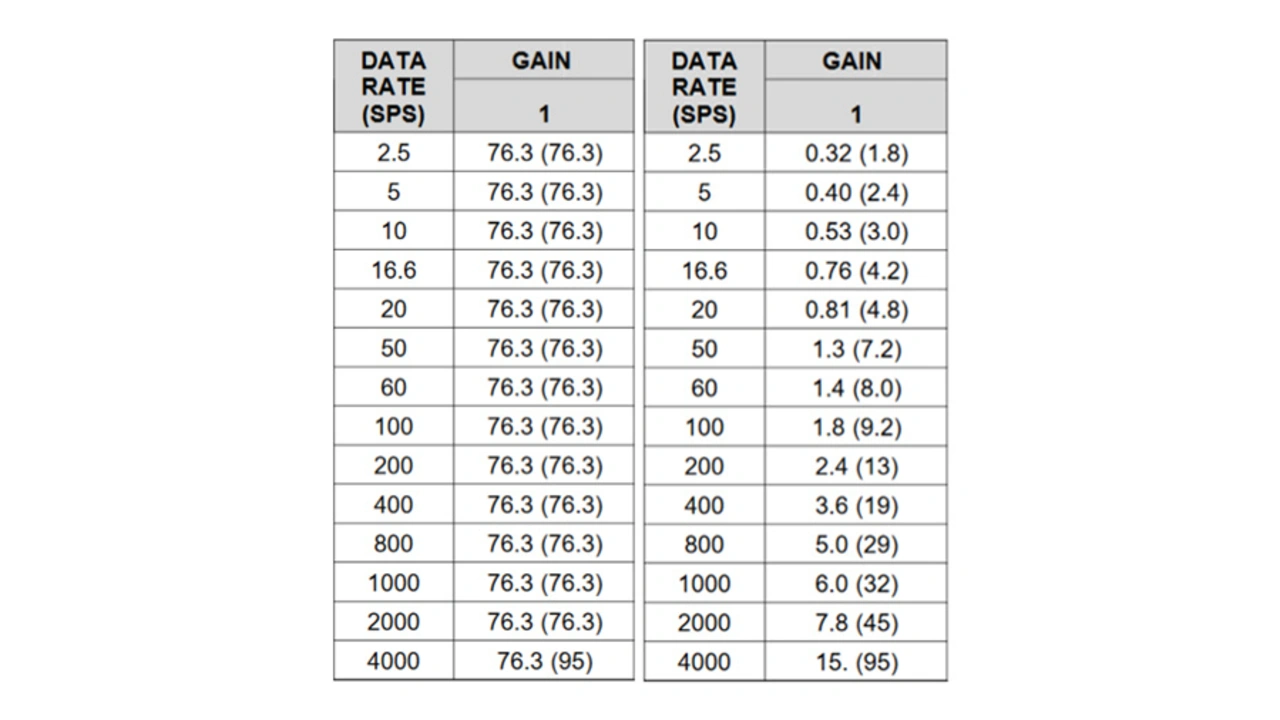
In der Rauschtabelle (Bild 6) für die 16-bit-Version ADS114S08 sind sämtliche eingangsbezogenen Rauschquellen unabhängig von der Datenrate identisch. Im Vergleich zu den eingangsbezogenen Rauschwerten des 24-bit-ADUs ADS124S08 [2] zeigt sich, dass beim 24-bit-ADU alle Rauschwerte unterschiedlich sind und sich mit abnehmender Datenrate verringern, d.h. verbessern.
Auch wenn hieraus an sich noch keine definitiven Schlussfolgerungen gezogen werden können, lässt sich mit den Gleichungen 3 und 4 die Größe des LSB für jeden ADU, bei einer Referenzspannung von 2,5 V, berechnen:
Daraus ergibt sich, dass das Rauschen des niedrigauflösenden 16-bit-ADU gemäß Datenblatt der Größe seines LSB entspricht, dem maximalen Quantisierungsrauschen. Die Rauschangaben im Datenblatt des hochauflösenden 24-bit-ADU dagegen sind deutlich größer als das Quantisierungsrauschen (1 LSB). Das Quantisierungsrauschen ist im Fall des hochauflösenden ADU so gering, dass es effektiv im thermischen Rauschen untergeht. Bild 6 stellt diesen Vergleich qualitativ dar.
- Einführung in die Rauscheigenschaften von Delta-Sigma-ADUs
- Wie kann ein Entwickler von dieser Erkenntnis profitieren?
- Übersicht der Abbildungen und Tabellen