Leistungswandler - Teil 1
Gekoppelte Induktivitäten und ihre Anwendungen
Mit diesem Fachbeitrag startet eine Serie über gekoppelte Induktivitäten. Zum Auftakt wird geklärt, wie diese Bauteile grundsätzlich funktionieren, welche Vor- und Nachteile sie haben und wie sie prinzipiell angewendet werden.
Zwei miteinander gekoppelte Induktivitäten können als separate Bauteile definiert werden, die sich einen Teil ihrer magnetischen Flusslinien teilen. Durch die gemeinsame Kopplung wird von der einen Wicklung eine Spannung in der anderen Wicklung induziert: Das wird gegenseitige Kopplung genannt.
Was ist der Unterschied zwischen einem Transformator oder Übertrager und einer gekoppelten Induktivität?
Leider sind zwischenzeitlich auch die Begriffe Transformator und Übertrager nicht mehr in ihrer konkreten Anwendung differenzierbar. Der Übertrager, eigentlich als Bauelement zur »Übertragung« und Impedanz-Anpassung von Signalen gedacht, wird ja heutzutage durchaus auch zur Übertragung von Energie, d.h. Spannung und Strom, im »transformatorischen« Sinne eingesetzt, deshalb wird im Folgenden nur der Begriff »Transformator« verwendet.
Die beiden Bauelemente – gekoppelte Induktivität und Transformator – sind sich, oberflächlich gesehen, sehr ähnlich. Deren Parameter jedoch werden unterschiedlich optimiert. Durch die unterschiedliche Namensgebung – gekoppelte Induktivität und Transformator – sollen die unterschiedlichen Verwendungszwecke verdeutlicht werden.
Natürlich sagen letztendlich nur die Datenblätter, welche Parameter die Bauelemente im Konkreten haben und wo sie eingesetzt werden können. Ein Transformator ist speziell für die Übertragung von Leistung von einer Wicklung auf die andere vorgesehen. Die Kopplung zwischen den beiden Wicklungen muss dazu so gut wie möglich sein und die Streuinduktivität soll gegen Null gehen. Die absolute Induktivität der einzelnen Wicklung ist für diese Art der Anwendung oft von untergeordneter Bedeutung.
Ein Transformator überträgt die Energie direkt von der Primärwicklung zur Sekundärwicklung, ohne die Energie im Magnetkreis zu speichern. Dazu fließt der Strom gleichzeitig in beiden Wicklungen, ihre magnetischen Flüsse sind entgegengesetzt gepolt und heben sich auf. Standardtransformatoren sind normalerweise mit einer festen Kopplung ausgeführt, die Werte von über 99 % annehmen kann.
Üblicherweise werden Transformatoren zur Leistungsübertragung verwendet, bei denen eine Verringerung der Kopplung zu Verlusten und einem schlechten Wirkungsgrad führt. Gekoppelte Induktivitäten sind in unterschiedlich starken Kopplungen verfügbar, von sehr geringer Kopplung, typisch nur 5 % bis 10 % bis zu über 90 %.
Bei einem Transformator wird normalerweise eine Wechselspannung an die Primärwicklung angelegt, um eine Spannung an der Sekundärseite zu erzeugen, die Stromübertragung erfolgt hier sofort. Jeder Teil an Energie, der gespeichert wird, wird in der Regel als Problem angesehen, denn er verursacht Verluste. Die meisten Transformatoren sind auf Kernen mit niedrigem magnetischen Widerstand (Reluktanz) gewickelt. Die Kerne haben zwar Magnetisierungs- und Streu-Induktivitäten, diese resultieren jedoch aus parasitären Effekten.
Ein idealer Transformator hat diese parasitären Eigenschaften nicht, ein idealer Transformator speichert keine Energie. Eine gekoppelte Induktivität kann je nach Ausführungsform Energie speichern. Die Induktivität ist dann dafür ausgelegt, eine beträchtliche Energiemenge im Kernfluss zu speichern.
Aus diesem Grund hat der Kern einen Spalt, entweder einen diskreten Spalt oder einen verteilten, wie in einem Kern aus Eisenpulver, in dem diese Energie als Magnetfeld gespeichert wird. Zudem sind Ferritmaterial und Wicklungsaufbauten dem jeweiligen Typ der gekoppelten Induktivität angepasst.
Bei gekoppelten Induktivitäten wird jede Wicklung immer noch allein als die eigentliche Induktivität verwendet, obwohl natürlich die »gewisse gegenseitige Kopplung« auch eine schaltungstechnische Rolle spielt, andernfalls wären ja zwei separate Induktivitäten vorhanden. Im Allgemeinen ist bei gekoppelten Induktivitäten die Streuinduktivität weniger ein Problem.
In der Tat kann es nützlich sein, für jede Wicklung eine gewisse garantierte, geringe, nicht gekoppelte Induktivität oder Streuinduktivität zu haben. Die absolute Induktivität jeder Wicklung bei offener sekundärer Wicklung ist hier ein wichtiger Parameter, der genau festgelegt wird. Die meisten dieser gekoppelten Induktivitäten haben die gleiche Anzahl von Windungen – das heißt ein Übersetzungsverhältnis von 1:1, aber einige Sonderbauformen haben ein höheres Übersetzungsverhältnis von 1:50 und mehr.
Die gegenseitige Kopplung der Magnetkreise in einer gekoppelten Induktivität ist insofern interessant, als die von den Wicklungen erzeugten Magnetflüsse die gleiche Polarität und damit eine Addition haben, was bewirkt, dass der magnetische Fluss einen nicht zu vernachlässigenden Wert hat und magnetische Energie im Kern gespeichert wird. Bei einem Transformator ist die Kopplung insofern anders, als die Flüsse entgegenwirken und sich somit aufheben, sodass ein vernachlässigbarer Nettofluss im Magnetkreis verbleibt.
Anwendungen für gekoppelte Induktivitäten umfassen normalerweise Schaltkreise, die hauptsächlich separate Induktivitäten verwenden, bei denen jedoch eine gewisse Kopplung zwischen den zwei induktiven Schaltkreisen die Funktion in einem oder mehreren Schaltungsparametern begünstigt. Eine gekoppelte Induktivität kann zum Beispiel in einem Sperrwandler verwendet werden, wo sie die Energie speichert, während der Schalttransistor (MOSFET) eingeschaltet ist, und dann die Energie an den Ausgang abgegeben wird, wenn der Schalttransistor (MOSFET) ausgeschaltet ist.
Gekoppelte Induktivitäten ermöglichen eine Reihe weiterer Vorteile, wie beispielsweise eine wesentlich reduzierte Stromwelligkeit, eine Spannungstransformation, die Änderung der Impedanz einer Schaltung und eine galvanische Trennung. Die Anwendung in Schaltnetzteilen beispielsweise umfasst SEPIC-Wandler, Wandler mit galvanischer Trennung, Mehrphasen-Wandler und spezielle Wandlerschaltungen, die die negativen Eigenschaften des harten Schaltens abschwächen.
Die gekoppelte Induktivität hat jedoch auch Nachteile und diese führen dazu, dass die Induktivität beispielsweise bei Sperrwandlern mit etwas höheren Verlusten arbeitet und nicht ideale, z.B. gerundete, statt dreieckige Signalformen verursachen kann, was schaltungstechnisch berücksichtigt werden muss. Außerdem sind die Stromspezifikationen für eine gekoppelte Induktivität unterschiedlich, je nachdem, ob ihre Wicklungen in Reihe oder parallelgeschaltet sind.
Wenn beispielsweise die Wicklungen in Reihe geschaltet werden, ist die Ersatzinduktivität aufgrund der gegenseitigen Induktivität mehr als doppelt so groß wie die Nenninduktivität. Die Sättigungs- und Effektivstrom-Nennwerte müssen auf den Strom angewendet werden, der gleichzeitig durch beide Wicklungen fließt, sofern im Datenblatt nichts Anderes angegeben ist. Ein klares Verständnis der Funktionsweise und der Spezifikationen gekoppelter Induktivitäten ist deshalb unerlässlich, um diese Bauelemente optimal nutzen zu können.
Gegenkopplung und Kopplungsfaktor
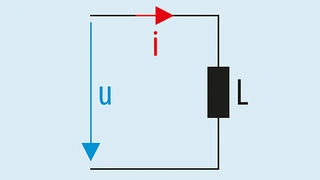
Eine einzelne Induktivität ist nur »an sich selbst gekoppelt«, das heißt, sie hat einen Eingang und einen Ausgang (html?aid=164807" href="https://www.elektroniknet.de/elektronik/power/bilder/gegenkopplung-und-kopplungsfaktor-bilder-1-4-8198.html?aid=164807">Bild 1), wobei Spannung und Strom der Beziehung nach Gleichung 1 folgen:
Die gekoppelte Induktivität besteht aus zwei Wicklungen oder Spulen, die sich einen gemeinsamen Kern teilen. Die Induktivität einer Wicklung ist abhängig vom Kernmaterial, der Geometrie des Kernmaterials, den Wicklungswindungen und der Art der Wicklungen. Da die beiden Wicklungen induktiv gekoppelt sind, beeinflussen sie sich gegenseitig. Die gegenseitige Induktivität zwischen den beiden Wicklungen kann ausgedrückt werden mit
wobei M die Gegeninduktivität, mit der Einheit H ist, und L1 und L2 die Induktivitäten der Primär- bzw. Sekundärwicklung sind.
Gegenkopplung und Kopplungsfaktor, Bilder 1-4
Das setzt jedoch voraus, dass eine perfekte Kopplung zwischen den Wicklungen ohne Streufluss besteht. In der Realität gibt es immer einen gewissen Streufluss, obwohl einige Konstruktionen extrem eng miteinander gekoppelt sind. Eine Zahl zum Ausdrücken der Kopplung zwischen den Wicklungen ist der Kopplungskoeffizient k. Er wird durch eine Zahl zwischen Null und Eins dargestellt, wobei k = 0 bedeutet, dass keine Kopplung vorliegt und k = 1 bedeutet, dass eine perfekte Kopplung vorliegt. Dieser Koeffizient kann verwendet werden, um die Gleichung 2 zu modifizieren, somit ergibt sich Gleichung 3.
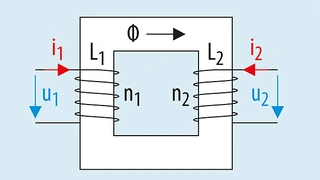
In gekoppelten Induktivitäten gibt es zwei Wicklungen, die sich einen einzigen Kern teilen und so miteinander gekoppelt sind. Dieses Prinzip ist vom Transformator bekannt und html?aid=164807" href="https://www.elektroniknet.de/elektronik/power/bilder/gegenkopplung-und-kopplungsfaktor-bilder-1-4-8198-Bild-2.html?aid=164807">Bild 2 verdeutlicht die Zusammenhänge. In Bild 2 bewirkt ein Strom i1 in der Induktivität L1 über den magnetischen Fluss Φ eine Spannung u2 in der Induktivität L2 auf der Sekundärseite des Transformators. Dieser Effekt wird als Gegeninduktivität bezeichnet und kann durch die Gleichung 4 beschrieben werden:
Somit besteht ein Transformator aus zwei magnetisch gekoppelten Induktivitäten, der Selbstinduktionsspannung und der gegenseitigen Induktionsspannung. Die Spannungen an den Induktivitäten können beschrieben werden mit:
und
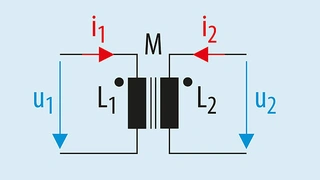
In Bild 3 ist das entsprechende Schaltbild dargestellt.
Die beiden Punkte an den Induktivitätssymbolen im Schaltbild geben die Wicklungsrichtung an. Die ideale Induktivität hat keine Verluste und kein Streufeld. Weder Verluste im Kupferdraht, noch im Ferritkern und im Isoliermaterial. Der Drahtwiderstand beträgt 0 Ω und der magnetische Widerstand des Ferritkerns beträgt 0 (μr -> ∞). Für diesen Fall gilt:
Somit gilt für den idealen Transformator, bzw. die gekoppelte Induktivität folgender Zusammenhang:
Das dazugehörige Schaltbild, des idealen Transformators, bzw. der idealen gekoppelten Induktivität zeigt Bild 4.
- Gekoppelte Induktivitäten und ihre Anwendungen
- Parasitäre Komponenten





