Startseite > E-Mechanik+Passive > Passive > Kernverluste genauer bestimmen

Induktive Bauelemente

Kernverluste genauer bestimmen

16. Juli 2015, 9:33 Uhr | Ralf Higgelke

▶ Diesen Artikel anhören

Fortsetzung des Artikels von Teil 1

Ermittlung der Verluste

Anfänglich wurden Kernverluste mithilfe der Gleichung (1) ermittelt, die sogenannte Steinmetz-Gleichung.

(1) $P subscript v space equals space K space times space f to the power of a space times space B subscript p k end subscript to the power of ß$

Hierbei sind P_V die Kernverluste (bedingt durch Hysterese und Wirbelströme) je Volumeneinheit, f die Frequenz, B_pk die maximale Flussdichte einer sinusförmigen Anregung (Amplitude) sowie K, α und β die Konstanten, die sich aus dem in Bild 2 gezeigten Kernverlustdiagramm ableiten.

Jobangebote+ passend zum Thema

Ingenieur/Elektroingenieur/Elektrotechniker als Field Application Engineer

GEYER Electronic GmbH, Planegg

Alle Jobangebote im Elektroniknet Karrierebereich anzeigen

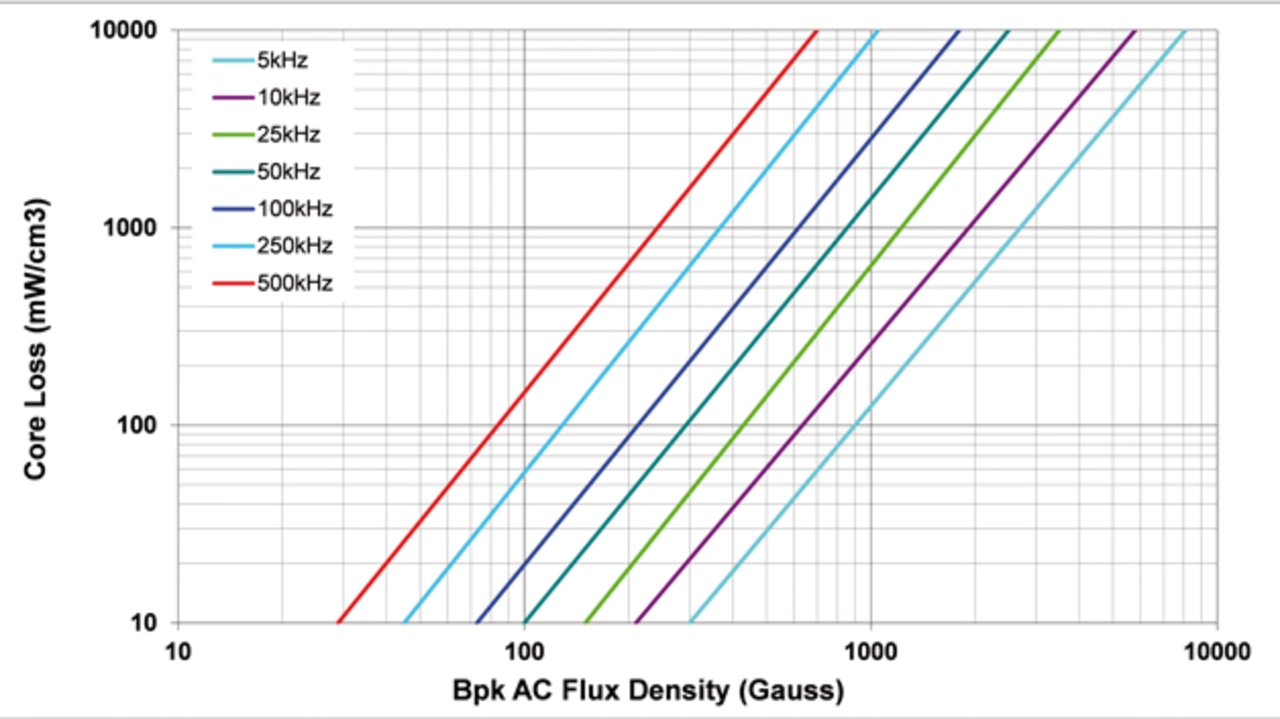
Die in Bild 2 für die Kernverluste angegebenen Daten umfassen gewöhnlich die Verluste sowohl der Hysterese als auch der Wirbelströme im Kern. Die Messung der Kernverluste ist schwierig, weil hierfür komplexe Aufbauten zur Messung der Flussdichte erforderlich sind und zudem eine Schätzung der Fläche der Hysteresekurve notwendig ist. Zum Zeichnen dieser Kurven wird eine Sinuswelle an den Ringkern mit ein oder zwei je eingängigen Spulenwicklungen angelegt. Dann werden viele Daten generiert, um das Kernverlustdiagramm zu erstellen.

Der wesentliche Nachteil der Steinmetz-Gleichung besteht darin, dass sie vor allem für sinusförmige Anregungen gilt. In Anwendungen der Leistungselektronik sieht sich die Spule beim Magnetfluss aber vor allem nichtsinusförmigen Wellenformen ausgesetzt. Zwar gibt es auch andere Modelle, die das Problem nichtsinusförmiger Wellenformen durch Trennung von Hysterese- und Wirbelstromverlusten zu lösen versuchen, doch hat sich die empirische Steinmetz-Gleichung als nützlichste Variante erwiesen und ist bei sinusförmige Wellenformen sehr genau und einfach zu handhaben.

Deswegen gibt es für diese Gleichung (1) Erweiterungen, die sie auch für nichtsinusförmige Wellenformen nutzbar machen sollen, beispielsweise die modifizierte Steinmetz-Gleichung (MSE, Modified Steinmetz Equation; Gleichung (2)).

(2) $P subscript v equals space open parentheses K space times space f subscript e q end subscript to the power of a minus 1 end exponent space times space B subscript p k end subscript to the power of ß close parentheses space times space f$

Dabei ist f_eq die äquivalente Frequenz bezogen auf die Änderung im Tastverhältnis für nichtsinusförmige Wellenformen. Aufgrund der mit der MSE einhergehenden Nachteile wurde dann die Verallgemeinerte Steinmetz-Gleichung (GSE, Generalized Steinmetz Equation) entwickelt (Gleichungen (4) und (5)).

(4) $P subscript v space equals space K space times space f subscript e q end subscript to the power of a minus 1 end exponent space times space B subscript e q end subscript to the power of ß$

(5) $B subscript e q end subscript space equals space 1 fourth space times space integral subscript 0 superscript T open vertical bar fraction numerator table row cell d B end cell end table over denominator d t end fraction close vertical bar space d t$

Aus diesem Grund basieren auch GSE- und MSE-Kernverlustdiagramme auf einer sinusförmigen Erregung. Es gelten zudem einige Einschränkungen, die weiter unten noch behandelt werden.

Es gibt auch noch eine Reihe alternativer Modelle, die von den Kernherstellern entwickelt wurden, die sich optimal für Kerne einsetzen lassen, die von genau diesen Herstellern hergestellt werden [5].

Folgende wesentliche Nachteile gelten für das Steinmetz-Modell und seine Erweiterungen:

Abhängigkeit von den empirischen Daten der Kernhersteller: Zum Erstellen von Kernverlustdiagrammen muss auf die Daten des Kernherstellers zurückgegriffen werden. Hersteller passiver Bauteile haben keinen Einfluss auf den Testaufbau.
Geringe Genauigkeit bei Puls- und Dreieckswellenformen, da die Kernverlustdiagramme auf Daten basieren, die durch eine sinusförmige Anregung entstehen.
Aufgrund von Fehlern bei der Parameterkonvertierung funktioniert die Erweiterung des Steinmetz-Modells nur bei einem Tastverhältnis von 50% und einem beschränktem Frequenzbereich optimal.
Beschränkung auf Bauteile, die aus bestimmten Materialien bestehen oder von bestimmten Herstellern stammen.
Wegen der hohen Komplexität bei der Schätzung der Magnetweglänge ist die Schätzung der Kernverluste mithilfe bestehender Modelle für Eisenpulver- und Metalllegierungsmaterialien nicht nur anspruchsvoll, sondern die Genauigkeit ist auch starken Schwankungen unterworfen.
Aufgrund der zeitlichen Veränderungen in der Magnetflussdichte entstehen auch in den Wicklungen Verluste infolge von Skin- und Proximity-Effekten usw. Die oben beschriebenen Ansätze berücksichtigen auch keine Wechselstromverluste der Wicklung.
Bei Bauteilen, die aus mehreren Materialien bestehen, ist eine Schätzung der Verluste nicht möglich.
Hohe Komplexität von Aufbauten, um empirische Daten ausreichender Genauigkeit zu ermitteln.