Startseite > Power > Spannungswandler > Eingangskondensatoren richtig dimensionieren

Gleichspannungswandler

Eingangskondensatoren richtig dimensionieren

9. Januar 2017, 14:53 Uhr | Von Manjing Xie

▶ Diesen Artikel anhören

Fortsetzung des Artikels von Teil 1

3. Auswahl der Kondensatoren

Auch wenn MLCCs hervorragende Eigenschaften bieten, um die Spannungswelligkeit zu reduzieren, so sind Ladekondensatoren mit großer Kapazität gefordert, um das gewünschte Verhalten bei Lastsprüngen zu erreichen. Aluminium-Elektrolyt- und Polymer-Kondensatoren mit hoher Kapazität sind kostengünstiger als die ausschließliche Verwendung von Keramikkondensatoren. Zwei wichtige Faktoren sind entscheidend für die Auswahl der großen Eingangskondensatoren, nämlich die zulässigen Über- und Unterschwinger bei Lastsprüngen sowie der zulässige Wechselstrom.

Matchmaker+ Anbieter zum Thema

zu Matchmaker+

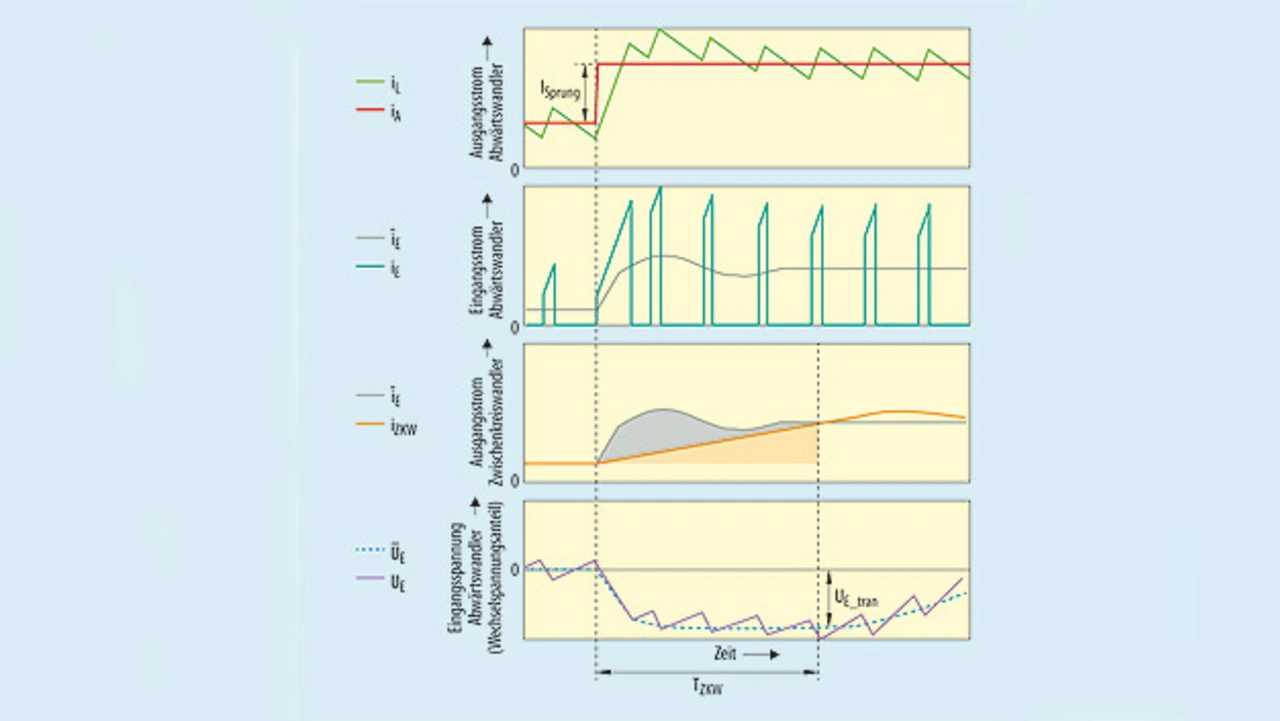
Der ESR des Ladekondensators (ESR_CEL) und seine Kapazität (C_EL) müssen den Anforderungen an die Lastsprungeigenschaften genügen. Bild 8 zeigt den idealisierten Lastsprung auf i_A, den Spulenstrom i_L, den transienten Eingangsstrom i_E und den Ausgangsstrom des Zwischenkreiswandlers i_ZKW. Der durchschnittliche Eingangsstrom ī_E lässt sich näherungsweise als Produkt aus i_L und dem Tastverhältnis (TV) errechnen.

Während des Lastsprungs können zwei Spitzen auf UE auftreten, von denen die erste mit dem äquivalenten Serienwiderstand des Ladekondensators (ESR_CEL) zusammenhängt, die zweite jedoch durch die Differenz zwischen dem mittleren Eingangsstrom des Abwärtswandlers (ī_E) und dem Ausgangsstrom des Zwischenkreiswandlers (i_ZKW) verursacht wird. Beide Spitzen sollten geringer sein als die zulässigen Über- und Unterschwinger (U_E,tran).

Der Wert von ESR_CEL sollte geringer sein als der mit Gleichung 4 errechnete Wert.

$left parenthesis 4 right parenthesis space space space space E S R subscript C E L space end subscript less or equal than fraction numerator U subscript E comma t r a n end subscript over denominator I subscript S p r u n g end subscript times T V subscript m a x end subscript end fraction$

Mit TV_max = 12,1 %, I_Sprung = 3 A und ΔU_E,tran = 0,36 V sollte ESR_CEL kleiner als 0,99 Ω sein.

Die zweite Spitze hängt mit dem Ansprechverhalten des Zwischenkreiswandlers zusammen. Die Anstiegszeit (T_ZKW) des Ausgangsstroms des Zwischenkreiswandlers lässt sich näherungsweise mit Gleichung 5 errechnen.

$left parenthesis 5 right parenthesis space space space space space T subscript Z K W end subscript space equals fraction numerator 1 over denominator B subscript R e g l e r end subscript space times space 4 end fraction$

Bei einer Regelbandbreite (B_Regler) von 6 kHz beträgt T_ZKW etwa 41,67 µs.
Die Kapazität des Ladekondensators C_EL sollte größer als der mit Gleichung 6 errechnete Wert sein.

$left parenthesis 6 right parenthesis space space space space C subscript E L end subscript greater or equal than fraction numerator begin display style 1 half end style times I subscript S p r u n g end subscript times D T V subscript m a x end subscript times T subscript Z K W end subscript over denominator U subscript E comma t r a n end subscript end fraction minus space C subscript C E comma t o t a l end subscript times left parenthesis 1 minus T o l. right parenthesis space space$

Darin steht C_CE,total für die Gesamtkapazität der Keramikkondensatoren am Eingang des Abwärtswandlers. Die Toleranz der Keramikkondensatoren am Eingang beträgt 10 %. C_EL sollte somit größer als 15,07 µF sein. Mit einer Bauteiltoleranz von 20 % sollte die Nennkapazität des Ladekondensators folglich größer als 18,84 µF gewählt werden.

Ein weiteres Kriterium für die Auswahl des Ladekondensators ist der zulässige Wechselstrom. Üblicherweise haben die meisten kostengünstigen Aluminium-Elkos eine deutlich höhere Impedanz als die Keramikkondensatoren, die zur Ableitung des Wechselstroms dienen. Es ist also davon auszugehen, dass die Welligkeitsspannung vom Ladekondensator nicht beeinflusst wird. Näherungsweise berechnen lässt sich der Wechselstrom im Ladekondensator (Δi_CEL), indem die Wechselspannung am Eingang durch ESR_CEL dividiert wird. Da der Wechselstrom einen dreieckförmigen Verlauf hat, lässt sich der Effektivwert des Wechselstroms (I_CEL,eff) mit Gleichung 7 abschätzen.

$left parenthesis 7 right parenthesis space space space space I subscript C E L comma e f f end subscript space equals fraction numerator 1 over denominator 2 square root of 3 end fraction times fraction numerator increment U subscript E comma S S end subscript over denominator E S R subscript C E L end subscript end fraction$

Zum Berechnen der Welligkeitsspannung am Eingang dient Gleichung 8.

$left parenthesis 8 right parenthesis space space space space increment U subscript E comma S S end subscript almost equal to fraction numerator T V times left parenthesis 1 minus T V right parenthesis times I subscript A over denominator C subscript C E comma t o t a l end subscript times f subscript s times left parenthesis 1 minus T o l. right parenthesis end fraction$

Der Ladekondensator C_EL sollte so gewählt werden, dass der in der Schaltung auftretende Wechselstrom I_CEL,eff kleiner als der für den Kondensator maximal zulässige Wechselstrom I_CEL,eff,max ist.

$left parenthesis 9 right parenthesis space space space space I subscript C E L comma e f f comma m a x end subscript greater or equal than I subscript C E L comma e f f end subscript$

Der zulässige Wechselstrom und der ESR-Wert des Ladekondensators sollten somit dem mit Gleichung 9 aufgestellten Kriterium entsprechen (siehe Gleichung 10).

$left parenthesis 10 right parenthesis space space space space space I subscript C E L comma e f f comma m a x end subscript times E S R subscript C E L end subscript greater or equal than fraction numerator 1 over denominator 2 square root of 3 times increment U subscript E comma S S comma m a x end subscript end root end fraction$

Bei TV_max = 12,1 %, C_CE,total = 6,6 µF und einer Toleranz von 10 % beträgt die maximale Wechselspannung am Eingang (ΔU_E,SS,max) etwa 179 mV. Das Produkt aus dem zulässigen Wechselstrom und dem ESR sollte deshalb größer sein als die nach Gleichung 9 berechneten 51,7 mV.

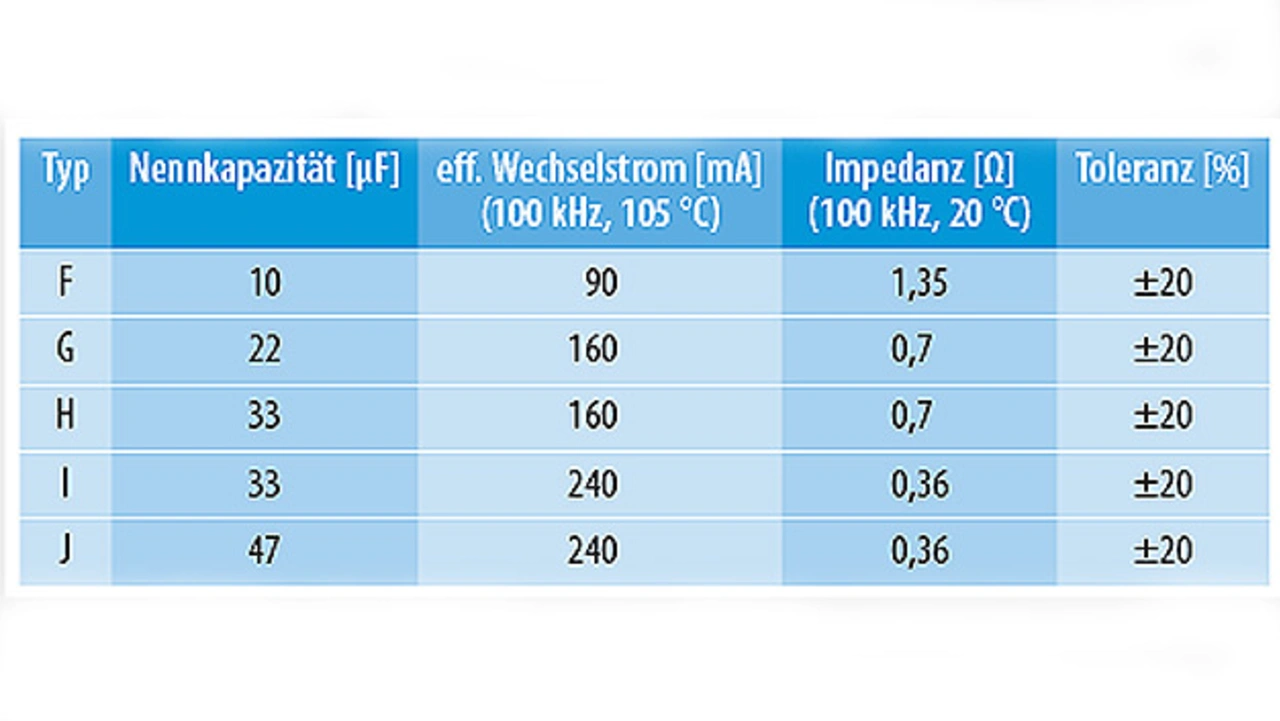
In Tabelle 2 wurden die Kenndaten von fünf verschiedenen Elektrolytkondensatoren zusammengefasst. Um die Transienten- und Welligkeitsstrom-Vorgaben zu erfüllen, wurde Kondensator G aus Tabelle 2 als Eingangskondensator für das Dimensionierungsbeispiel gewählt. In Anwendungen, in denen ein Elko allein nicht ausreicht, können mehrere Elkos parallelgeschaltet werden, um die Transienten-Anforderungen zu erfüllen.

Das Kriterium für das Produkt aus dem zulässigen Wechselstrom und ESR_CEL bleibt jedoch unverändert. Wenn kein Elektrolytkondensator die Wechselstromanforderungen erfüllt, werden zusätzliche Keramikkondensatoren benötigt. Die Kapazität dieser zusätzlichen Keramikkondensatoren lässt sich mit den Gleichungen 8 und 9 berechnen.

Bei all diesen Überlegungen darf ein Aspekt aber nicht übersehen werden: Entscheidend für die Leistungsfähigkeit des Schaltwandlers ist auch ein korrektes Leiterplattenlayout [2].

Literatur

[1] TPS5331x High-Efficiency, 8-A or 14-A, Synchronous Buck Converter with Eco-mode Control. Texas Instruments, Datenblatt, 2015, www.ti.com/lit/ds/symlink/tps53318.pdf.
[2] Taylor, R.: Power Tips: Don’t let your power supply layout ruin your day! Texas Instruments, TI E2E Community, Blogs, Power House, e2e.ti.com/blogs_/b/powerhouse/archive/2015/01/23/don-t-let-your-power-supply-layout-ruin-your-day.
[3] Simpson, C.: Engineers Note: Capacitors are key to voltage regulator design. Texas Instruments, Dokument Nr. SNOA842, 2011, www.ti.com/lit/wp/snoa842/snoa842.pdf.

Die Autorin

Manjing Xie
ist Applikationsingenieur für Stromversorgungen im Bereich Power Design Services bei Texas Instruments. Sie hat mehr als zehn Jahre Erfahrung in der Entwicklung von AC/DC- und DC/DC-Wandlern sowie in der Entwicklung von Leistungshalbleitern. Xie hat ihr Elektrotechnikstudium an der Tsinghua-Universität, Peking, China, mit dem Bachelor (BSEE) und an der Virginia Polytechnic Institute and State University (Virginia Tech), Blacksburg, USA, mit dem Master (MSEE) abgeschlossen.

Manjing Xie

ist Applikationsingenieur für Stromversorgungen im Bereich Power Design Services bei Texas Instruments. Sie hat mehr als zehn Jahre Erfahrung in der Entwicklung von AC/DC- und DC/DC-Wandlern sowie in der Entwicklung von Leistungshalbleitern. Xie hat ihr Elektrotechnikstudium an der Tsinghua-Universität, Peking, China, mit dem Bachelor (BSEE) und an der Virginia Polytechnic Institute and State University (Virginia Tech), Blacksburg, USA, mit dem Master (MSEE) abgeschlossen.

asktexas@ti.com