Würth Elektronik eiSos
Ferrite für die EMV
Fortsetzung des Artikels von Teil 1
Derating und Resonanzeffekte
Die unterschiedlichen Materialien eignen sich für verschiedenen Frequenzbereiche. Eisenpulver (Fe) ist bei niedrigen Frequenzen am effektivsten. Bei Ferrit hingegen gibt es zwei Typen, MnZn für den mittleren Frequenzbereich und NiZn für den hohen Frequenzbereich. Die Besonderheit an Ferrit ist, dass oberhalb einer materialspezifischen Frequenz (z. B. 10 MHz) der Realteil des Verlustwiderstandes dominiert. Daraus können sich in Abhängigkeit der an das Filter angeschlossenen Impedanz folgende Vorteile ergeben:
- Der Ferrit arbeitet im ohmschen Bereich (µ“) als »Absorber« für Frequenzen über etwa 10 MHz, das Nutzsignal im Bereich unter 10 MHz wird nicht beeinflusst.
- Die Tiefpassfilterung von drahtgewickelten Ferriten oder SMD-Ferriten wird in Verbindung mit einer niederimpedanten Filterlast erreicht.
- Breitbandige Störunterdrückung ist mit »nur« einer Komponente erreichbar,
- kein kapazitiver Einfluss auf Daten- oder Signalleitungen.
Jobangebote+ passend zum Thema
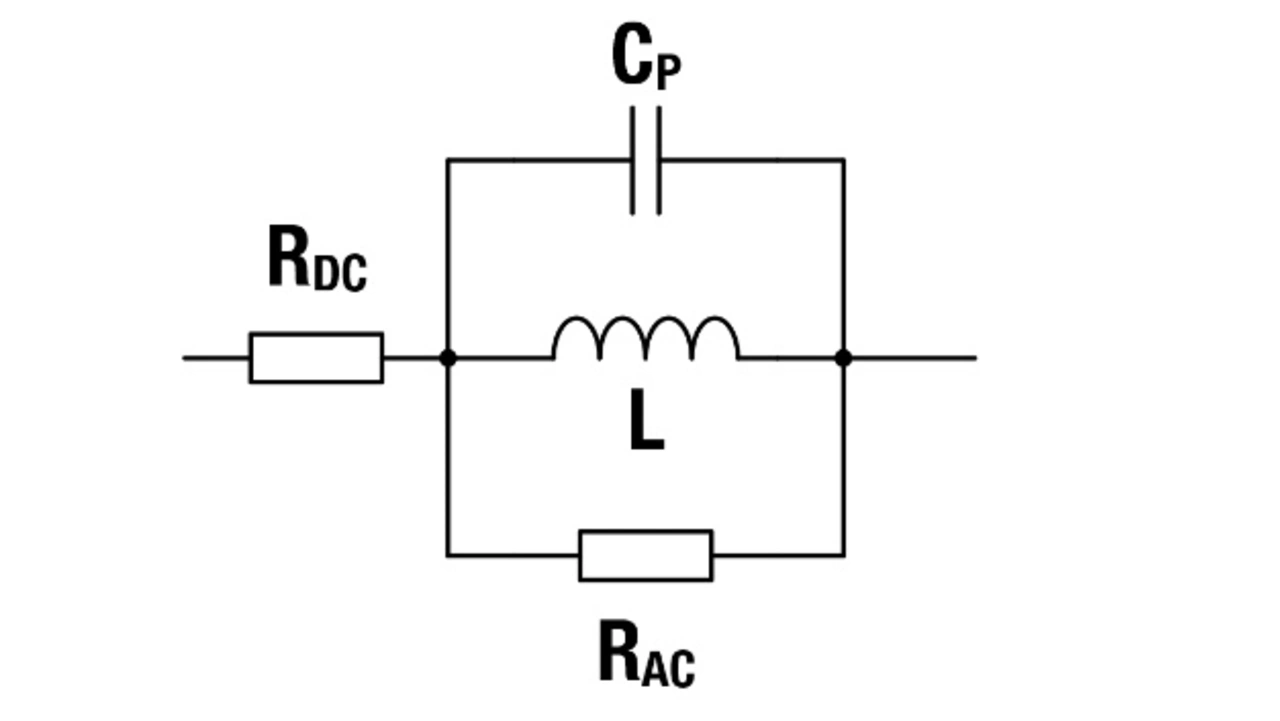
Dazu ist jedoch notwendig, dass die an das Filter angeschlossene kapazitive Last als Teil des frequenzabhängigen Spannungsteilers fungiert und damit bekannt sein muss. Neben ihrer Induktivität haben alle induktiven Bauelemente auch einen ohmschen Widerstand (sowohl bezüglich Wechselstrom als auch bezüglich Gleichstrom) und eine Kapazität. Zusammen bilden jene die parasitäre Impedanz (Bild 6).
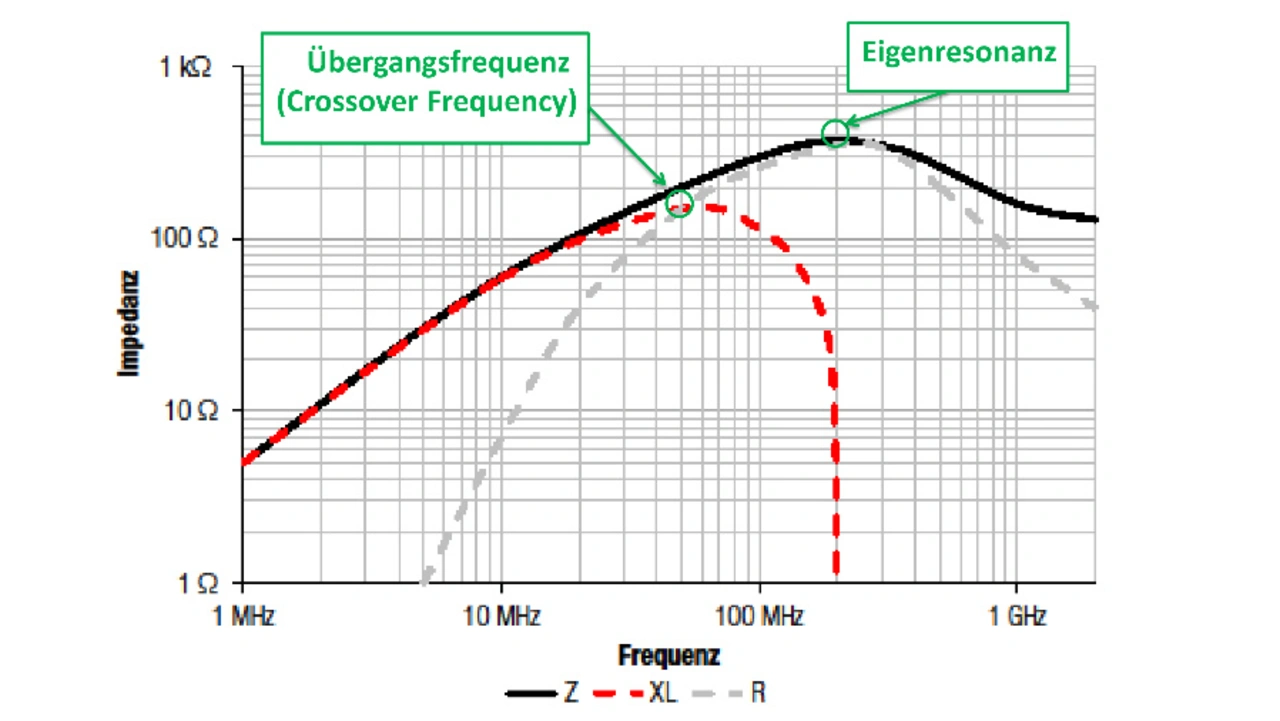
Bei der Übergangsfrequenz (Crossover Frequency) sind die induktive Reaktanz und der Widerstand im Diagramm betragsmäßig gleich, nicht aber in ihrer Phasenlage (Bild 7). Unterhalb dieser Frequenz ist die induktive Reaktanz höher, sodass sich das Bauelement wie eine Induktivität verhält. Jenseits dieser Frequenz ist der resistive Anteil betragsmäßig höher, sodass das Bauteil den Strom in diesem Frequenzbereich in Wärme umwandelt. Dies funktioniert bis zu Eigenresonanzfrequenz. An diesem Punkt gerät die Induktivität mit der parasitären Kapazität der Wicklung in Resonanz, was die Impedanz stark erhöht. Über diesen Punkt hinaus wirkt das Bauteil kapazitiv und seine Effektivität nimmt ab.
Derating und Resonanzeffekte
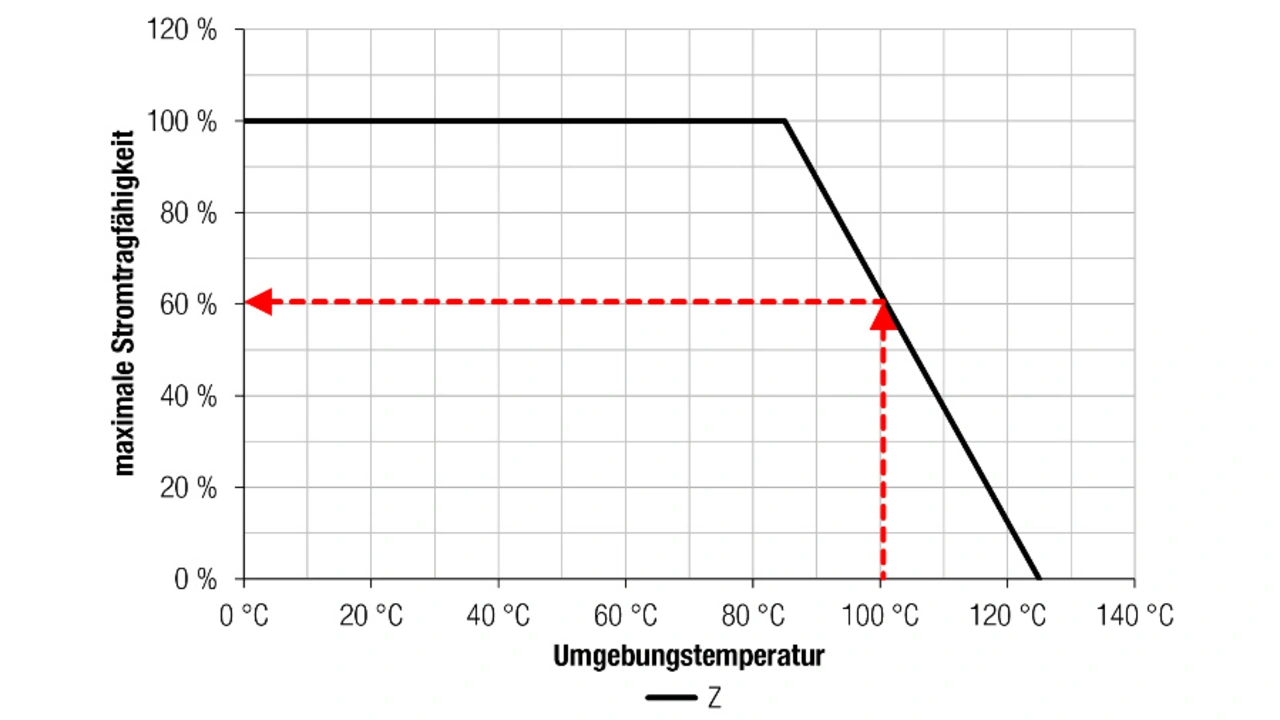
Die Strombelastbarkeit der Induktivität ist aus zwei Gründen zu beachten. Erstens ist sie thermisch begrenzt, der Leiter kann also nur eine begrenzte Stromstärke übertragen, ohne zu heiß zu werden. Daher spezifizieren die Hersteller in den Datenblättern den »Nennstrom«. Dies ist der Strom, der dazu führt, dass die Temperatur der Induktivität um einen bestimmten Betrag steigt, typischerweise um 40 K gegenüber der Umgebung. In Kombination mit einer Umgebungstemperatur von +85 °C beträgt die maximale Betriebstemperatur +125 °C. Um bei einer höheren Umgebungstemperatur arbeiten zu können, ist der Nennstrom zu reduzieren – Derating genannt. Dadurch fällt der Temperaturanstieg nicht so groß aus und das Bauteil bleibt innerhalb der maximal zulässigen Betriebstemperatur. Um beispielsweise bei einer Umgebungstemperatur von +100 °C arbeiten zu dürfen, müsste der Strom unter Verwendung der Derating-Kurve in Bild 8 auf 60 % reduziert werden, um den Temperaturanstieg auf maximal +125 °C zu begrenzen.
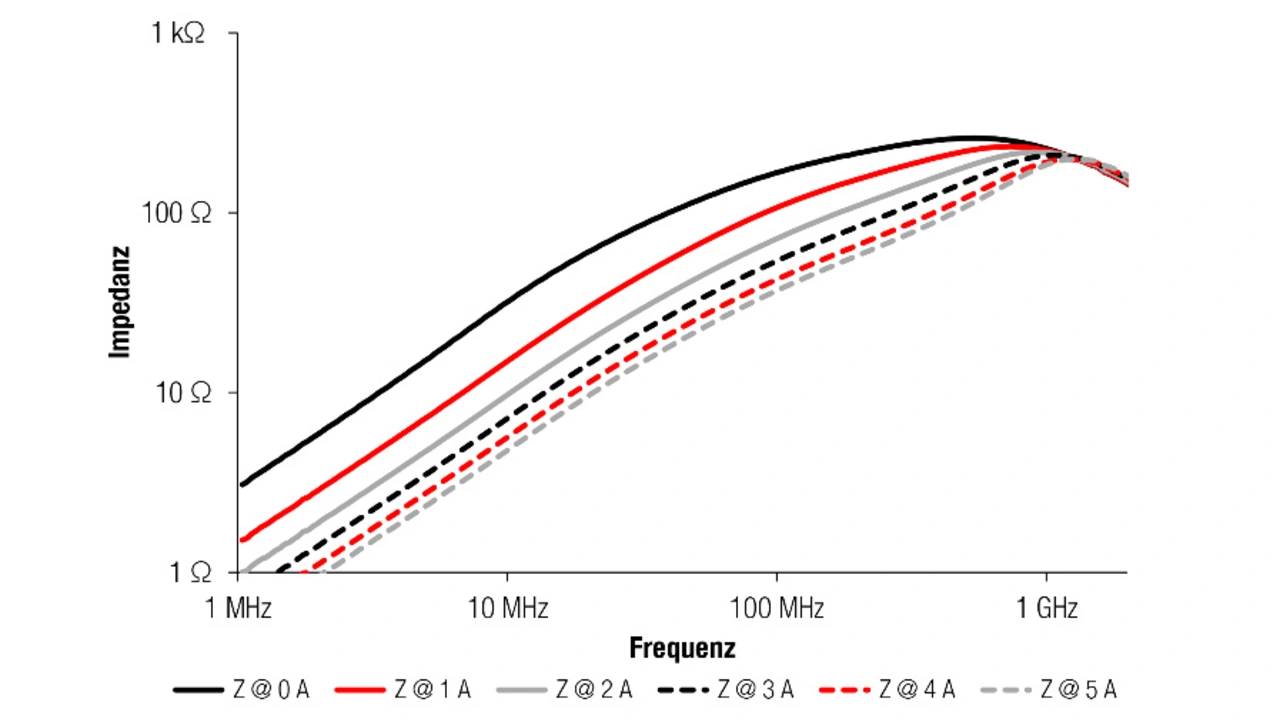
Die zweite Überlegung ist der Vormagnetisierungsstrom (DC-Bias). Alle Ferritperlen werden bei einem Vormagnetisierungsstrom von Null gemessen, also wenn kein Strom durch diese fließen. Im realen Filterbetrieb bei Stromversorgungen ist der Strom durch die Ferritperlen jedoch niemals gleich Null. Mit steigendem Strom nimmt die Impedanz ab, da der Kern durch den Gleichstrom vormagnetisiert wird und sich somit der Sättigung nähert. Große Induktivitäten spezifizieren einen maximalen Vormagnetisierungsstrom insofern, dass Induktivität um einen definierten Prozentsatz abgefallen ist. Zu beachten ist, dass es dafür keine Norm gibt, die diesen Parameter spezifiziert. Daher liegt dieser Prozentsatz bei vielen Herstellern irgendwo zwischen 10 % und 40 %. Bei Ferritperlen verschiebt sich auch die Impedanzcharakteristik nach unten, sodass bei der Auswahl Vorsicht geboten ist (Bild 9).
Ein weiterer zu beachtender Nebeneffekt sind Resonanzspitzen. Diese resultiert aus der Wechselwirkung zwischen der Ferritperle und dem Entkoppelkondensator mit hoher Güte im Tiefpassfilter, dessen Resonanzfrequenz des Filters unterhalb der Übergangsfrequenz der Ferritperle liegt. Dies führt zu einer zu geringen Dämpfung und kann Teile der Restwelligkeit und des Störsignals sogar verstärken anstatt sie zu dämpfen. Unterhalb der Übergangsfrequenz genügt die ohmsche Komponente nicht, um ausreichend zu dämpfen. In diesen Fällen ist es notwendig, zusätzlich zu dämpfen. Drei Möglichkeiten stehen dafür zur Verfügung:
- Hinzufügen eines Widerstands in Serie zum Entkoppelkondensator, was jedoch dessen Wirkung mindert.
- Hinzufügen eines Widerstands parallel zur Ferritperle, was jedoch deren Wirksamkeit mindert.
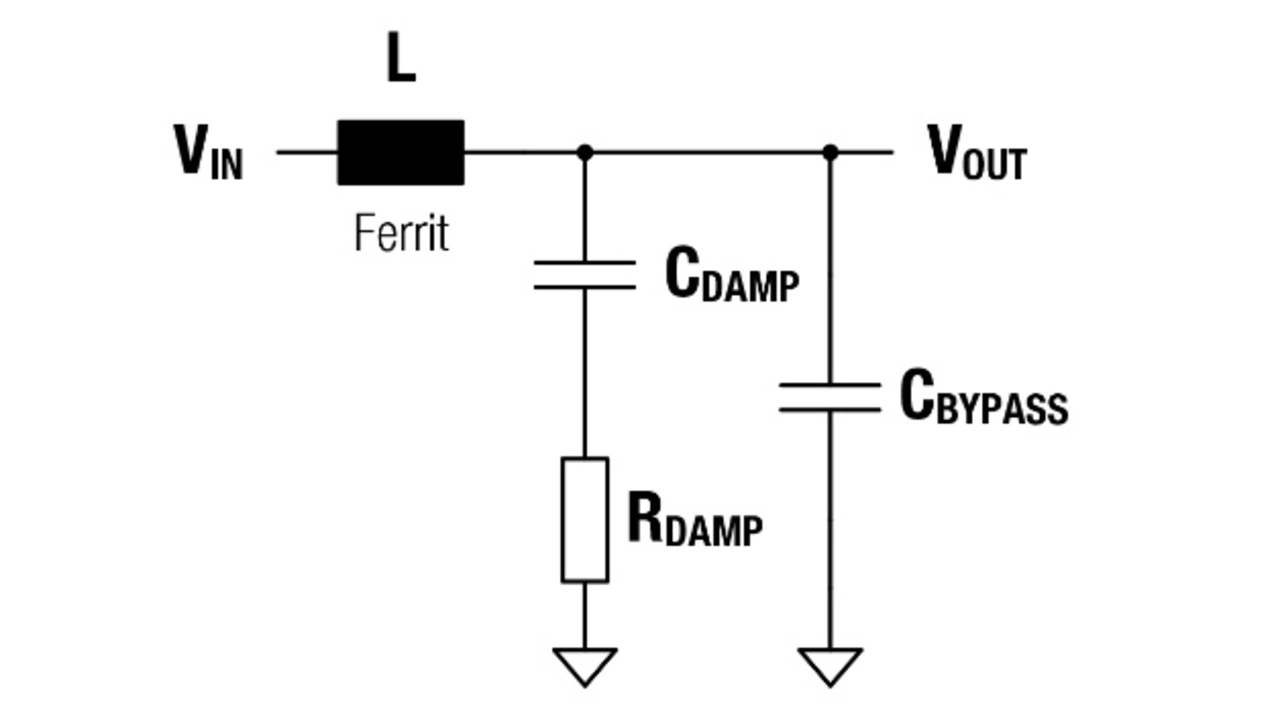
- Hinzufügen eines großen Kondensators mit seriellem Dämpfungswiderstand parallel zum Entkoppelkondensator (Bild 10). Dies verschlechtert das Filter nicht, und der große Kondensator verhindert, dass im Widerstand die Verlustleistung zu hoch wird.
Zu beachten ist, dass Ferritperlen jeweils für verschiedene Anwendungsbereiche optimiert sind. Entscheidend ist das Zusammenspiel von Ferritmaterial und Wicklungsstruktur. Der Vorteil der SMD-Ferrite besteht darin, dass sie sich direkt auf der Leiterplatte in unmittelbarer Nähe der Störquelle platzieren lassen, was den besten Effekt erzielt. SMD-Ferrite lassen sich nach folgenden Anwendungsbereichen klassifizieren:
- High-Speed-SMD-Ferrite haben eine geringere Impedanz im unteren Frequenzbereich, um eine geringe Dämpfung für schnelle Signale zu erzielen.
- Breitband-SMD-Ferrite zeigen eine hohe Impedanz im niedrigen Frequenzbereich. Daher arbeiten sie breitbandig über das gesamte Frequenzspektrum.
- HF-SMD-Ferrite haben eine modifizierte interne Anordnung, um den effektiven Entstörfrequenzbereich zu erhöhen. Folglich ist die Impedanz bei 1 GHz bis zu dreimal höher.
- Hochstrom-SMD-Ferritperlen sind für Ströme über 1 A ausgelegt. Der Nennstrom bezieht sich auf 40 K Eigenerwärmung.
- SMD-Ferritperlen mit hoher Pulsfestigkeit sind so konzipiert, dass sie wiederkehrende hohe Einschaltströme ohne Ausfall überstehen.
Anwendung von Ferrit-Bauelementen
Eigentlich lässt sich die richtige Auswahl des Ferrits nur durch Messungen im EMV-Labor bestätigen. Denn nur so kann festgestellt werden, welche Frequenz zu dämpfen ist. Bei einer hochfrequenten elektronischen Schaltung ist es generell nicht möglich, die dynamische Impedanz (Systemimpedanz) zu berechnen. Denn sie hängt von vielen Faktoren ab, die mathematisch schwer zu beschreiben sind, insbesondere im HF-Bereich. Nichtsdestotrotz kann die Vorauswahl mit vergleichenden Messungen und Erfahrungen unter Berücksichtigung folgender Punkte getroffen werden:
- Frequenzbereich des Störsignals,
- Quelle des Störsignals,
- Benötigte Dämpfung,
- Umgebungs- und elektrische Parameter der Schaltung (Umgebungstemperatur, Vormagnetisierungsstrom, maximaler Betriebsstrom, Frequenz des Nutzsignals),
- Platz auf der Platine.
Die Dämpfung A kann folgendermaßen berechnet werden:
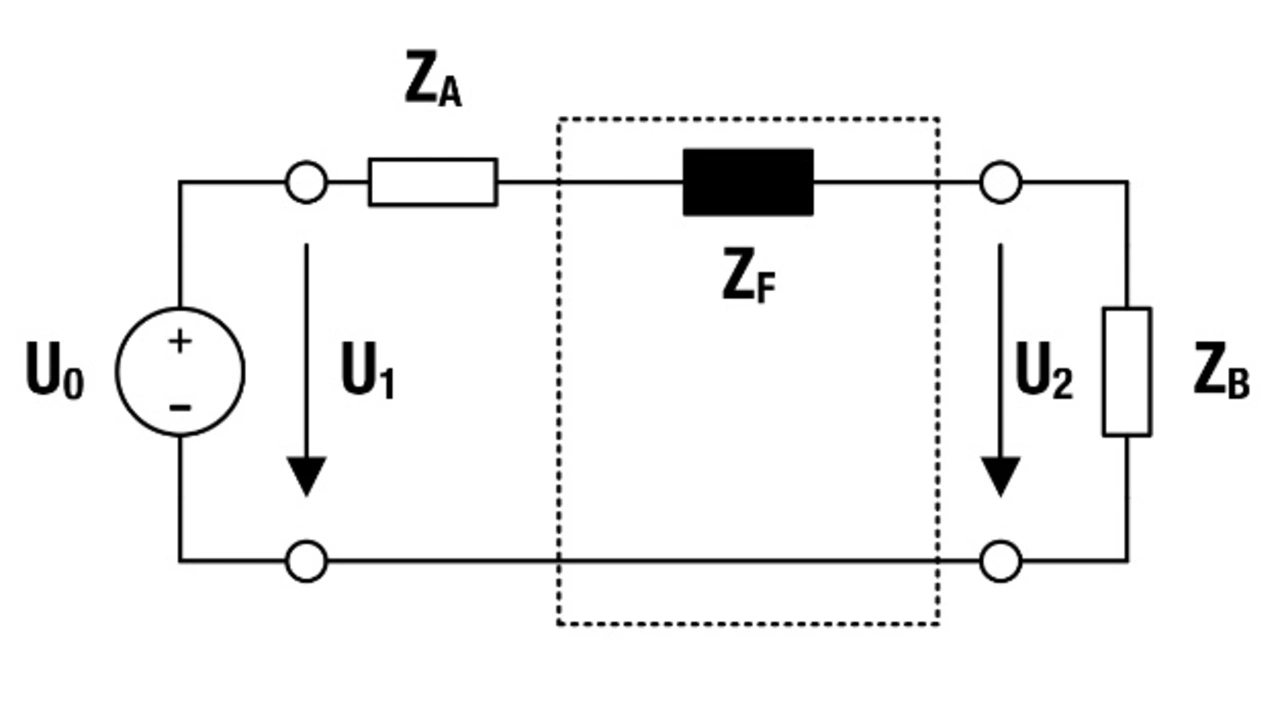
Zunächst sind die Systemimpedanzen ZA (Quelle) und ZB (Last) und die erforderliche Störunterdrückung A zu bestimmen (Bild 11). Die Impedanz des Ferritbauteils ZF lässt sich berechnen, wenn man obige Gleichung nach ZF umstellt:
Je nach benötigter Impedanz und Anwendung kann der Ferrittyp und das richtige Bauelement ausgewählt werden. Als Hilfsmittel zur Bestimmung der Systemimpedanzen, die nicht immer vorhanden sind, lassen sich die Werte aus Tabelle 1 verwenden.
| Anwendung | Angenommene praxisnahe Systemimpedanz |
|---|---|
| Masse (GND) | 1 Ω |
| Spannungsversorgung (VCC) | 10 Ω |
| Signalleitungen | 50 Ω bis 90 Ω |
| Lange Datenleitungen | 90 Ω bis 150 Ω |
Tabelle 1: Praxisnahe Systemimpedanzen.
Hier ein einfaches Beispiel aus der Praxis: Bei 125 MHz ist an einer Stromversorgungsschnittstelle mit 1 A Gleichstrom eine zusätzliche Dämpfung von 12 dB erforderlich. Aus der letzten Gleichung lässt sich mithilfe der Werte aus Tabelle 1 die Impedanz des Ferritbauteils ZF zu 59,6 Ω bestimmen. Die Ferritperle 74279215 aus der Serie WE-CBF von Würth Elektronik eiSos hat bei 125 MHz eine Impedanz von etwa 75 Ω und ist für 3 A ausgelegt. Dies ist unter Berücksichtigung des Vormagnetisierungsstroms bei einem Gleichstrom von 1 A vorteilhaft.
Ein letzter Punkt zu Tiefpassfiltern. Im Zeitbereich steigen die Anstiegs- und Abfallzeiten des Signals, im Frequenzbereich reduziert sich die Amplitude der höherfrequenten Oberwellen. Bei Mikroprozessoranwendungen ist darauf zu achten, dass die Flanken der digitalen Signale nicht zu langsam verlaufen, da dies im Falle von zeitkritischen Schaltungen die Funktion beeinträchtigen kann.
Fazit
Zusammenfassend lässt sich sagen, dass die Impedanzkurven der Hersteller die Auswahl der richtigen Bauteile vereinfachen. Bei der Verwendung von Ferriten für EMV-Applikationen ist das effektivste Ferritmaterial für den relevanten Frequenzbereich, der Nennstrom, ein eventueller Vormagnetisierungsstrom, die Betriebstemperatur und die spezifische Art der Anwendung (High Speed, breitbandig, Leistung) in Betracht zu ziehen. Weiterhin sind mögliche unbeabsichtigte Nebeneffekte wie Eigenresonanz oder Nutzsignalverzerrungen zu berücksichtigen. Die korrekte Verwendung von Ferritperlen ist eine effektive und kostengünstige Möglichkeit, hochfrequente Störungen zu reduzieren.
WEITERFÜHRENDE LITERATUR
- T. Brander, A. Gerfer, B. Rall, H. Zenkner, Trilogie der induktiven Bauelemente (fünfte Auflage), Würth Elektronik eiSos, ISBN: 978-3-934-35030-4.
- H. Ott, Electromagnetic Compatibility Engineering, Wiley, ISBN: 978-0-470-18930-6.
- J. Eco, A. Limjoco, Ferrite Beads Demystified, Analog Dialogue 50-02, February 2016.
- C. Burket, All ferrite beads are not created equal – Understanding the importance of ferrite bead material behavior, In Compliance, August 2010.
- Ferrite für die EMV
- Derating und Resonanzeffekte
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Elektromagnetische Verträglichkeit
DC-DC-Wandler zeit- und kostensparend entstören
Jetzt Vorträge einreichen!
„Anwenderforum EMV“ - Call for Papers läuft!
Aktion »Elektronik Leser testen«
Zehn Praxistester für Powermanagement-Baukästen gesucht!
Jetzt Vorträge einreichen!
„Anwenderforum EMV“ - Call for Papers eröffnet
EMV-Filter für Umrichter
Gleichtaktdrossel und Gegentaktdrossel in Einem
Kondensatoren / Intertec Components
MLCCs richtig messen
Leistungswandler - Teil 2
Gekoppelte Induktivitäten und ihre Anwendungen
Forschungstransfer
Würth Elektronik und Uni Hannover gewinnen Gold
Leistungswandler - Teil 1
Gekoppelte Induktivitäten und ihre Anwendungen
Unternehmenskultur
Fehler erlaubt: Zwei Führungskräfte über den »eiSos-Spirit«
Technologiezentrum in München
Würth Elektronik eiSos investiert dreistelligen Millionenbetrag
How-to-Video / Würth Elektronik
Der Nennstrom einer Induktivität einfach erklärt
Speicherinduktivitäten
EMV bei Schaltreglern sicherstellen
Übertrager für Schaltregler-Designs
Trafos für Sperrwandler
