Mit nichtlinearen Kapazitäten umgehen
Schaltungs-Design mit Planar- und Superjunction-MOSFETs
Fortsetzung des Artikels von Teil 1
Physikalische Gesetze – ein Gedankenspiel
Anstatt grundlegende physikalische Gesetze in Zweifel zu ziehen, ist es vielleicht lehrreicher, sich diese nochmals genauer anzusehen und sich zu vergewissern, ob sie im vorliegenden Kontext auch korrekt angewandt werden. Ein kleines Gedankenexperiment macht die Sache interessant: Wenn zwei parallelgeschaltete Kondensatoren auf die gleiche Spannung aufgeladen sind und exakt die gleiche Ladung speichern, folgt daraus dann zwingend, dass sie auch die gleiche Energiemenge speichern?
Gemäß den wohlbekannten Gleichungen Q = CU und E = ½ CU2 müsste die Antwort ein klares „ja“ sein. Man könnte meinen, dass das Ergebnis für jede Spannung gilt, auch für nichtlineare Kapazitäten. Leider sind die vertrauten Gleichungen für gespeicherte Ladung und Energie nicht universell gültig – sie gelten nur für den Sonderfall konstanter Kapazität. Auf einer fundamentaleren Ebene definiert, ist die Kapazität gleich der Ladungsänderung pro Spannungsänderung und die Spannung gleich der Energieänderung pro Ladungsänderung, also C = dQ/dU und U = dE/dQ.
Jobangebote+ passend zum Thema
Unter der impliziten Voraussetzung konstanter Kapazität lassen sich aus den obigen Gleichungen die vereinfachten Gleichungen für Ladung und Energie ableiten. Im Falle nichtlinearer Kapazitäten müssen Ladung und Energie durch Integration der Kapazität bzw. der Ladung über die Spannung berechnet werden.
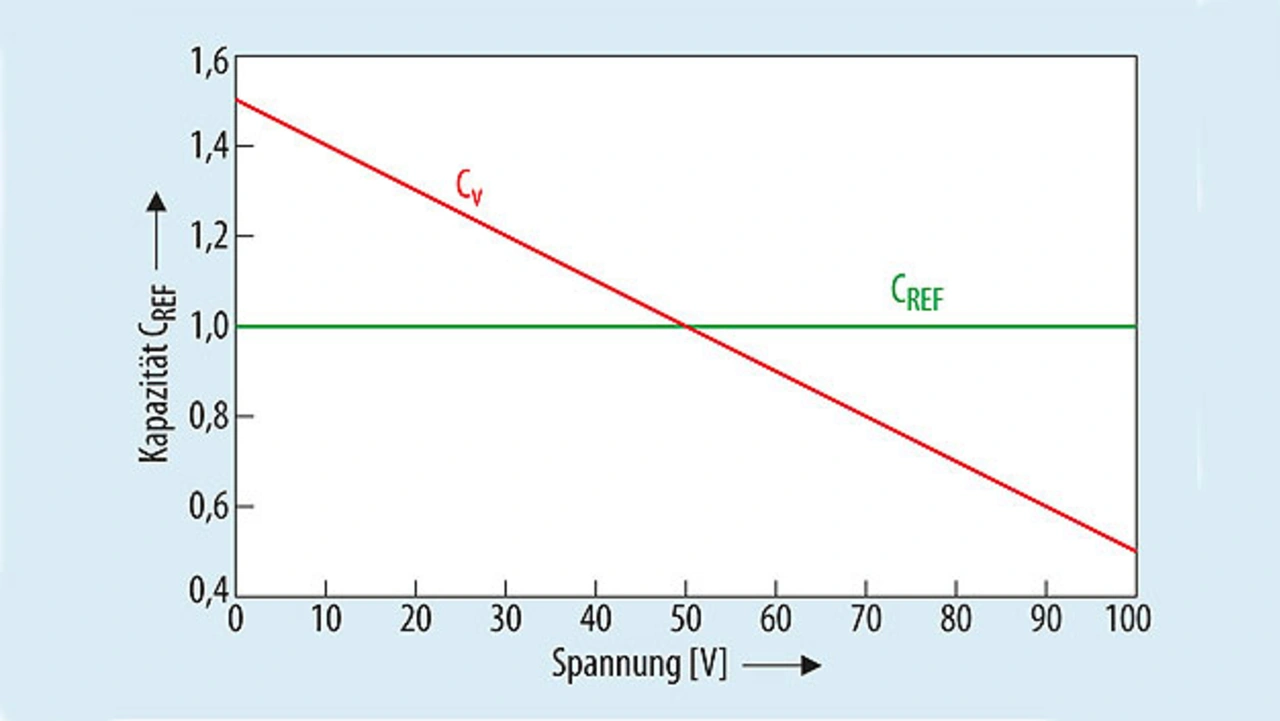
Bild 3 soll das verdeutlichen. Die Kurven zeigen die Kapazität zweier Kondensatoren in Abhängigkeit von der anliegenden Spannung. Die Kapazität des Referenzkondensators CREF ist spannungsunabhängig. Die Kapazität des Kondensators CV ändert sich im Bereich zwischen 0 V und 100 V linear von 1,5∙CREF bis 0,5∙CREF. Bei 100 V speichern beide Kondensatoren die gleiche Ladungsmenge. Das ist daran zu erkennen, dass die Fläche (C ∙ U) unter den beiden Kurven in diesem Fall für beide Kondensatoren gleich groß ist. Die gespeicherten Energiemengen sind hingegen unterschiedlich.
Integriert man die gespeicherte Ladung über die Spannung, so stellt sich heraus, dass CREF bei 100 V nur 83,3 % der Energie von CV speichert. Ebenso lässt sich zeigen, dass CV bei 75 V 10 % mehr Ladung, aber die gleiche Energiemenge wie CREF speichert.
Zwei äquivalente Kapazitäten
Mit diesen Integrationen arbeiten MOSFET-Hersteller schon seit Jahren. Allerdings spezifizieren sie die Ergebnisse nicht als Ladung und Energie, sondern rechnen sie in zwei verschiedene äquivalente Kapazitäten um: COTR ist eine feste Kapazität, die beim Aufladen auf 80 % von UDSS die gleiche Ladungsmenge wie COSS enthält. COER ist eine feste Kapazität, die bei Aufladung auf 80 % von UDSS die gleiche Energiemenge wie COSS enthält.
In [4] wird eine empirisch ermittelte, effektive COSS bei 80 % der Nennspannung beschrieben, die der zeitbezogenen äquivalenten Kapazität entspricht. Allerdings differenziert der Applikationsbericht nicht zwischen COTR und COER, die sich bei heutigen MOSFETs weitaus stärker voneinander unterscheiden als früher und individuell betrachtet werden müssen. Dabei ist zu beachten, dass sowohl COTR als auch COER selbst von der anliegenden Spannung abhängig sind.
Das Integral einer nichtlinearen Funktion ist stets wieder eine nichtlineare Funktion. Deshalb wird dieser Wert in den Datenblättern auf eine bestimmte Spannung bezogen, beispielsweise auf 80 % der Nenn-Sperrspannung UDS oder auf 400 V. Die Tatsache, dass es für ein und dieselbe COSS zwei verschiedene äquivalente Werte gibt – einen für die gespeicherte Ladung und einen für die gespeicherte Energie – liefert die Antwort auf das Rätsel.
COTR und COER sind nicht nur unterschiedlich groß, das Verhältnis der beiden Werte kann sogar als Maß für die Nichtlinearität dienen. In dem genannten Beispiel mit einer Kapazitätsschwankungsbreite von 1,5:0,5 unterscheiden sich COTR und COER um 16,7 %. Beim SiHP15N60E beträgt das Verhältnis COTR/COER fast 3,6. Bei anderen Superjunction-MOSFETs kann die Kapazitätsschwankungsbreite größer als 100:1 und das Verhältnis COTR/COER größer als 10 sein.
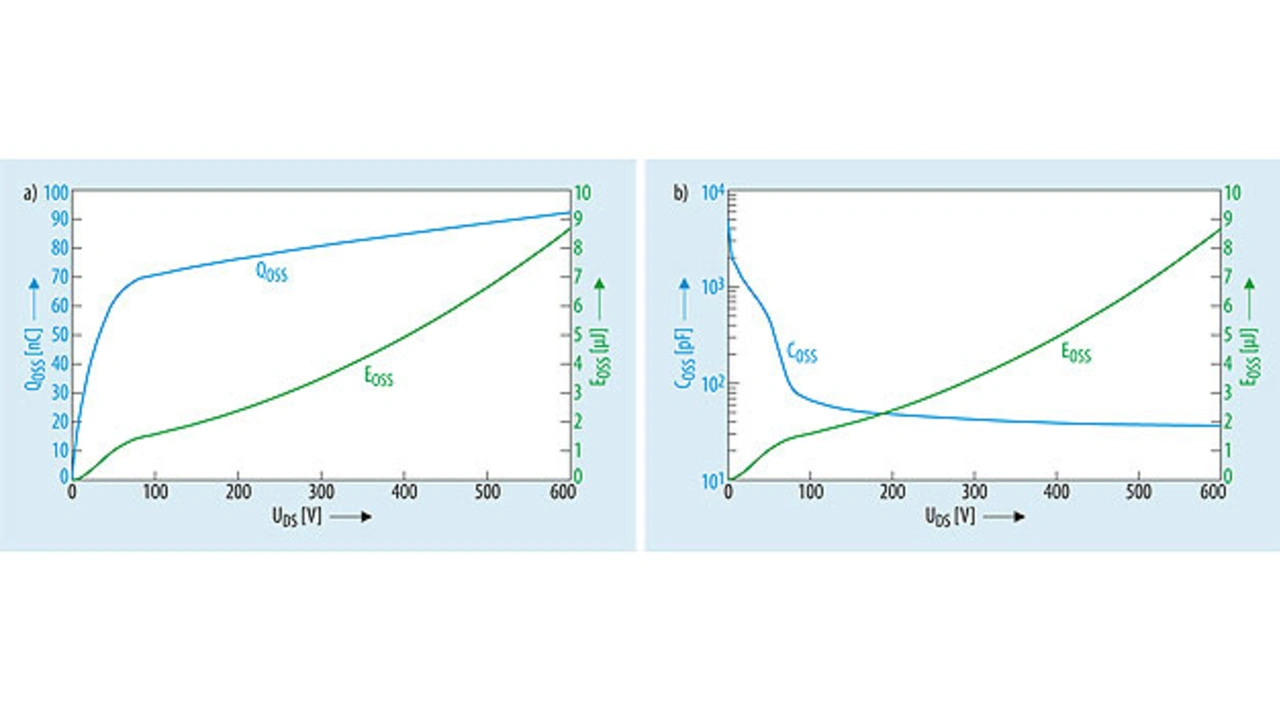
Bild 4a zeigt die gespeicherte Ladung und die gespeicherte Energie in Abhängigkeit von der Spannung für den SiHP15N60E. Obwohl die beiden Parameter eng miteinander zusammenhängen, unterscheiden sie sich hinsichtlich ihrer Spannungsabhängigkeit drastisch voneinander. Die im Verhältnis sehr große Kapazität COTR und die entsprechend große gespeicherte Ladungsmenge muss in allen Brückenschaltungen berücksichtigt werden – insbesondere in solchen, die im ZVS-Modus arbeiten.
Das Entladen des MOSFET-Ausgangskondensators ist nicht gleichbedeutend mit Energieentzug, und für die Dimensionierung der Schaltung sollte nicht COER, sondern COTR herangezogen werden. Selbstverständlich werden für die Berechnung der Schaltverluste sowohl die Berechnungen COER als auch der Energie benötigt [3].
Damit ist klar, dass der Absolutwert von COSS bei einer gegebenen Spannung nicht mehr aussagekräftig ist, also wertlos für die Anwender. Nicht die Kapazität selbst interagiert mit dem Rest der Schaltung, sondern die gespeicherte Ladung und die gespeicherte Energie bestimmen das Verhalten. Sieht man sich Schaltungsberechnungen an, in denen COSS vorkommt, stellt man fest, dass dieser Wert durch Multiplikation mit den entsprechenden Spannungsfaktoren in die gespeicherte Ladung oder Energie umgerechnet wird.
Mehr Informationen im Datenblatt
Zur Unterstützung von Systementwicklern veröffentlichen MOSFET-Hersteller, darunter auch Vishay, jetzt in ihren Datenblättern zu Hochspannungs-MOSFETs außer COTR und COER auch die vollständigen EOSS-Kurven (Bild 4b). Für 100-V-MOSFETs wird in der Regel auch die Ladung QOSS bei 50 % spezifiziert, um die Totzeitanalyse für 48-V-ZVS-Brücken zu erleichtern.
Ähnliche Erwägungen gelten auch für die Gate-Drain-Kapazität CRSS, deren Wert jedoch wesentlich kleiner als COSS ist. Wie bereits eingangs erwähnt, ist dieser Wert definitionsgemäß in den COSS-Messwerten enthalten. Die nichtlineare Natur von CRSS wurde schon vor langer Zeit als problematisch erkannt und in der Fachliteratur abgehandelt. Die QGD-Komponente der Gate-Ladungskurve ist nichts anderes als die in CRSS gespeicherte Gesamtladung, die beim Ein- bzw. Ausschalten zugeführt bzw. entnommen werden muss.
Zu beachten ist, dass die Nichtlinearität der (stückweise linearen) Gate-Ladungskurve nicht auf Nichtlinearitäten der beteiligten Kapazitäten zurückzuführen ist. Beim Einschalten eines MOSFETs ist das Laden zweier verschiedener Kondensatoren erforderlich, an denen während des ausgeschalteten Zustands unterschiedlich hohe Spannungen anliegen [2].
Beim Einsatz von MOSFETs sollte man sich stets darüber im Klaren sein, dass deren Kapazitäten nicht aus zwei Elektroden mit einem Dielektrikum dazwischen bestehen. Stattdessen sind sie von transienter Natur und kommen hauptsächlich während der Schaltintervalle ins Spiel, wenn der MOSFET schnellen Spannungsänderungen dU/dt ausgesetzt ist.
Die in Ersatzschaltbildern dargestellten Kapazitäten repräsentieren die Interaktionen zwischen elektrischen Feldern in Halbleitermaterialien und den damit einhergehenden Strömen. Die Darstellung ist nur aussagekräftig, solange die Beziehung linear ist. Angesichts der hohen Nichtlinearitäten bei heutigen MOSFETs könnte man auch sagen, dass es so etwas wie COSS oder CRSS eigentlich nicht mehr gibt.
Die Integration der Kapazitätskurven lässt keine Schlüsse darauf zu, wie diese Kapazitäten mit dem Rest der Schaltung interagieren. Der Versuch, die Kurve zu linearisieren und zu glätten, macht also keinen Sinn. Stattdessen sollten Entwickler direkt mit gespeicherten Ladungen und Energien arbeiten.
Literatur
[1] Sanjay Havanur and Philip Zuk. “Power MOSFET Basics: Understanding Superjunction Technology” Vishay Application Note AN-849, April 2015, http://www.vishay.com/docs/66864/an849.pdf
[2] Sanjay Havanur “Power MOSFET Basics: Understanding the Turn On Process” Vishay Application Note AN-850, June 2015, http://www.vishay.com/docs/68214/turnonprocess.pdf
[3] Sanjay Havanur, “Beware of Zero Voltage Switching” April 2016 Newsletter, http://www.how2power.com/pdf_view.php?url=/newsletters/1604/articles/H2PToday1604_design_VishaySiliconix.pdf
[4] International Rectifier “More Realistic Characterization of Power MOSFET Output Capacitance COSS” AN-1001, 1999. http://www.infineon.com/dgdl/an-1001.pdf?fileId=5546d462533600a401535590a5c70f36
[5] Shen, Z. John, Yali Xiong, Xu Cheng, Yue Fu, and Pavan Kumar. „Power MOSFET switching loss analysis: a new insight.“ 2006 IEEE Industry Applications Conference Forty-First IAS Annual Meeting, vol. 3, pp 1438-1442.
[6] M. Orabi, A. Abou-Alfotouh and A. Lotfi “Coss Capacitance Contribution to Synchronous Buck Converter Losses” Power Electronics Specialists Conference (PESC), 2008, pp 666-672
[7] Drofenik, U., A. Muesing, and J. W. Kolar. „Voltage-dependent capacitors in power electronic multi-domain simulations.“ Proc. 2010 Int. Power Electron. Conf. (ECCE Asia), pp. 643-650. 2010.
[8] Costinett, Daniel, Regan Zane, and Dragan Maksimovic. „Circuit-oriented modeling of nonlinear device capacitances in switched mode power converters.“ Control and Modeling for Power Electronics (COMPEL), 2012 IEEE 13th Workshop on, pp. 1-8. IEEE, 2012.
[9] Elferich, Reinhold. „General ZVS half bridge model regarding nonlinear capacitances and application to LLC design.“ 2012 IEEE Energy Conversion Congress and Exposition (ECCE), pp 4404-4410.
[10] “Coss related energy loss in power MOSFETs used in zero-voltage-switched applications”, JB Fedison et al, IEEE Applied Power Electronics Conference and Exposition (APEC), 2014, pp 150-156
[11] Roig, Jaume, and Filip Bauwens. „Origin of Anomalous Hysteresis in Resonant Converters with Superjunction FETs.“ IEEE Transactions on Electron Devices 62, no. 9 (2015), pp 3092-3094.
[12] Fedison, J. B., and M. J. Harrison. „Coss hysteresis in advanced superjunction MOSFETs.“ 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), pp 247-252.
Der Autor
Sanjay Havanur
arbeitet als Senior Manager Systems Applications bei Vishay Siliconix. Er ist IEEE-Mitglied, hält sieben Patente im Bereich Leistungsumwandlung und ist Autor mehrerer technischer Veröffentlichungen. Havanur hat einen Hochschulabschluss in Elektrotechnik und einen Master in Leistungselektronik; beide Abschlüsse absolvierter er am Indian Institute of Technology.
- Schaltungs-Design mit Planar- und Superjunction-MOSFETs
- Physikalische Gesetze – ein Gedankenspiel
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
2. Anwenderforum Leistungshalbleiter
Dr. Gerald Deboy und Dr. Alex Lidow halten die Keynotes
LTspice von Vishay
Entwicklung einer PTC-basierten Schutzvorrichtung
Vishay
IR-Empfänger für die Wohnrealität
Hochspannungs-SiC-Wechselrichter
Zur Stabilisierung von Mittelspannungsverteilnetzen
Isolierte Gate-Treiber
Tore öffnen – aber wie?
Obsoleszenz-Probleme lösen
SiC-Kaskoden ersetzen Si-MOSFETs
Infineon
Neues Entwicklungszentrum für Automotive und KI in Dresden
Kommentar von Prof. Leo Lorenz
Entwicklungstrends in der Leistungselektronik
