Präzise Messwerterfassung
Was beim Einsatz von ADUs mit hoher Auflösung zu beachten ist
Fortsetzung des Artikels von Teil 1
Die Auswirkungen des Rauschens der Eingangsstufe
Da die Rauschquellen üblicherweise nicht korrelieren, lassen sie sich nach dem RSS-Verfahren (Root Sum Square) addieren. Je stärker das Rauschen in der Eingangsstufe ist, umso mehr dominiert es das Gesamtrauschen (RMS, Root Mean Square). Addiert sich eine Rauschquelle von 5 nV zu einer weiteren Quelle von 3 nV, so ergibt sich ein RMS-Rauschen von 5,8 nV. An diesem Ergebnis ist die Dominanz der größeren der beiden Quellen zu erkennen.
Um einen besseren Eindruck zu bekommen, soll nun der Gesamt-Signal-Rauschabstand (SNR, Signal-to-Noise Ratio) berechnet werden, wobei aus Gründen der Einfachheit der SINAD (SINAD, Signal-to-Interference Ratio Including Noise and Distortion) außer Acht gelassen werden soll. Der SNR-Wert eines A/D-Umsetzers wird im Datenblatt üblicherweise in dB angegeben und lässt sich gemäß Gleichung 3 ausdrücken:
SNR = 6,02n+1,761
Darin steht n für die Auflösung in bit.
Um den SNR eines Operationsverstärkers, eines PGA oder eines Messverstärkers zu berechnen, ist zunächst das Gesamtrauschen nach der RSS-Methode zu berechnen (siehe Schaltung in Bild 1).
Jobangebote+ passend zum Thema
![Beschalteter Operationsverstärker (OPA189 [2]) zur Ermittlung des RMS-Rauschens und des SNR Beschalteter Operationsverstärker (OPA189 [2]) zur Ermittlung des RMS-Rauschens und des SNR](https://cdn.elektroniknet.de/thumbs/media_uploads/images/1597835381-270-woramyjmt.jpg.1280x0.webp)
Anstatt die verstärkungsbestimmenden Widerstände und die Gegenkopplungs-Widerstände einzeln zu betrachten, kann zum Berechnen des Rauschens die Parallelschaltung dieser Widerstände in Form des Ersatzwiderstands (RErsatz) herangezogen werden. RErsatz hat in diesem Fall einen Wert von 990 Ω und lässt sich für die Rauschberechnung mit 1 kΩ gleichsetzen.
Das thermische Rauschen der externen Widerstände berechnet sich nach Gleichung 4:
Darin ist kB die Boltzmann-Konstante (1,38 × 10-23 J/K) und T ist die absolute Temperatur, z.B. 298 K bei 25 °C.
Das thermische Rauschen eines Widerstandes lässt sich vereinfacht auch mit Gleichung 5 errechnen:
Mit R für den Widerstandswert in kΩ.
Bei einem 1-kΩ-Widerstand resultiert somit ein Wert von 4 nV/√Hz, bei 100 kΩ ein Wert von 40 nV/√Hz – und zwar jeweils bei einer Temperatur von 25 °C bzw. 298 K.
Der Operationsverstärker OPA189 [2] von Texas Instruments hat eine Rauschspannungsdichte UR’ von 5,2 nV/√Hz und eine Rauschstromdichte IR’ von 165 fA/√Hz bei 1 kHz. Der Anteil des Stromrauschens ergibt sich als
URausch, I = IR’ × R = 165 × 10-15 × 1 × 103 = 165 × 10-12.
Gleichung 6 drückt das Gesamtrauschen (URausch, RSS) wie folgt aus:
und ergibt einen Wert von 6,56 nV/√Hz.
Zur Berechnung des RMS-Rauschens am Ausgang wird zunächst die Bandbreite (B) des beschalteten Operationsverstärkers benötigt, die durch Gleichung 7 definiert wird:
Darin steht GBP für das Verstärkungs-Bandbreiten-Produkt und NG (Noise Gain) für die Rauschverstärkung. Durch das Einsetzen der Werte der Schaltung aus Bild 1 in Gleichung 7 ergibt sich 14 × 106/101 = 139 kHz. Das Gesamt-RMS-Rauschen wird daraufhin mithilfe von Gleichung 8 ermittelt:
Hierin steht NG wiederum für die Rauschverstärkung und BRauschen ist die Rauschbandbreite. Sie ist wie folgt definiert: BRauschen = 1,57 × fg = 218 kHz.
Durch Einsetzen der Werte in Gleichung 8 ergibt sich:
101 × 6,56 × 10-9 × √218000 = 310 µV.
In der Schaltungssimulation betrug das RMS-Rauschen 300 µV.
Mit Gleichung 9 wird der SNR des Operationsverstärkers berechnet:
Darin beträgt die Spannung zur Vollaussteuerung (FSR, Full Scale Range) (UFSR) 2,5 V und aus der vorherigen Berechnung wurde URausch, RMS = 310 µV ermittelt. Das Ergebnis der Rechnung ist 69,1 dB. Zum Vergleich: Die Schaltungssimulation lieferte 70,6 dB.
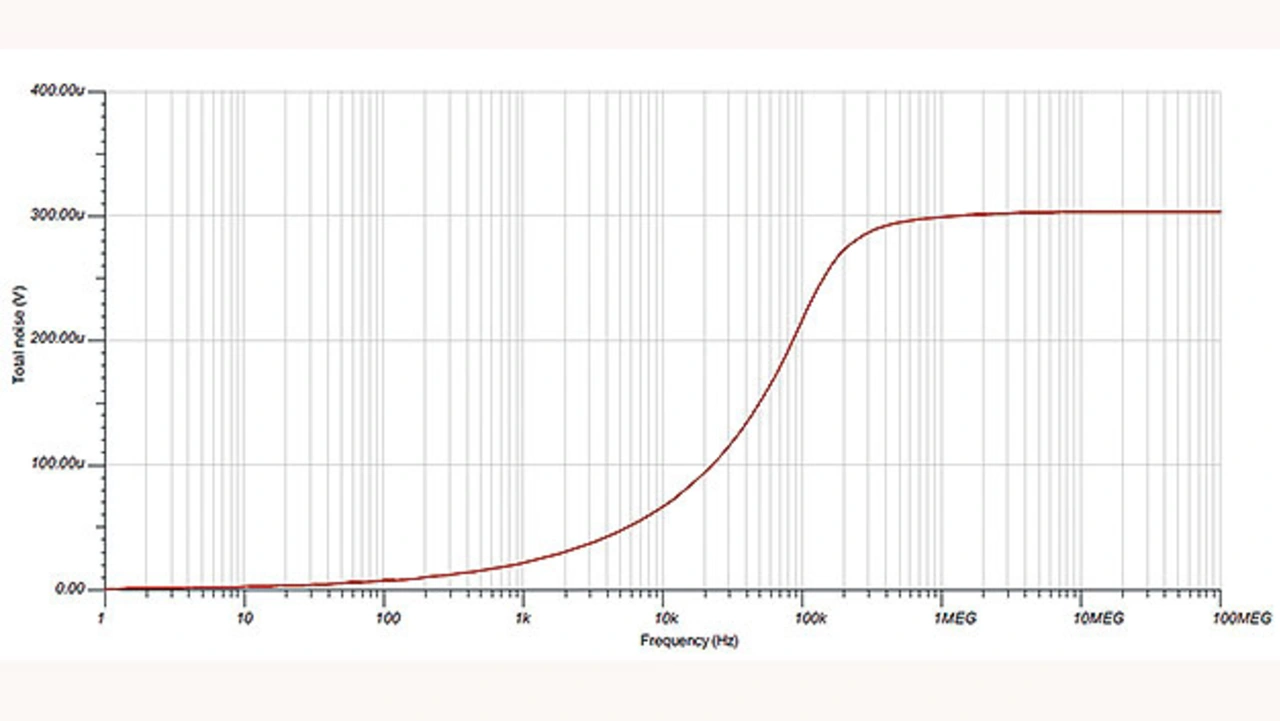
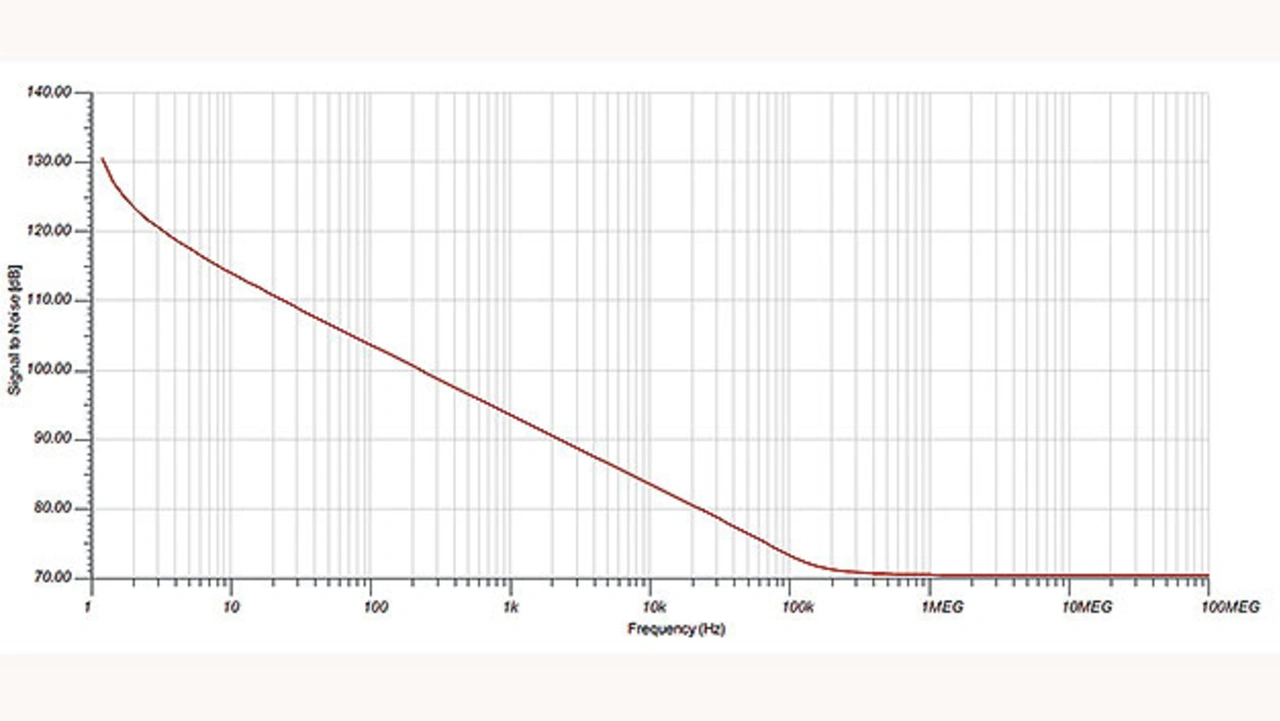
Die Bilder 2 und 3 zeigen das in der Schaltungssimulation ermittelte Gesamtrauschen (RMS) und den SNR abhängig von der Frequenz.
- Was beim Einsatz von ADUs mit hoher Auflösung zu beachten ist
- Die Auswirkungen des Rauschens der Eingangsstufe
- Auswirkungen auf den Analog-Digital-Umsetzer