Startseite > Power > Spannungswandler > Kapazitive Stromversorgungen auslegen

Kondensatoren

Kapazitive Stromversorgungen auslegen

5. November 2015, 10:46 Uhr | Ralf Higgelke

▶ Diesen Artikel anhören

Fortsetzung des Artikels von Teil 1

Eine kapazitive Stromversorgung berechnen

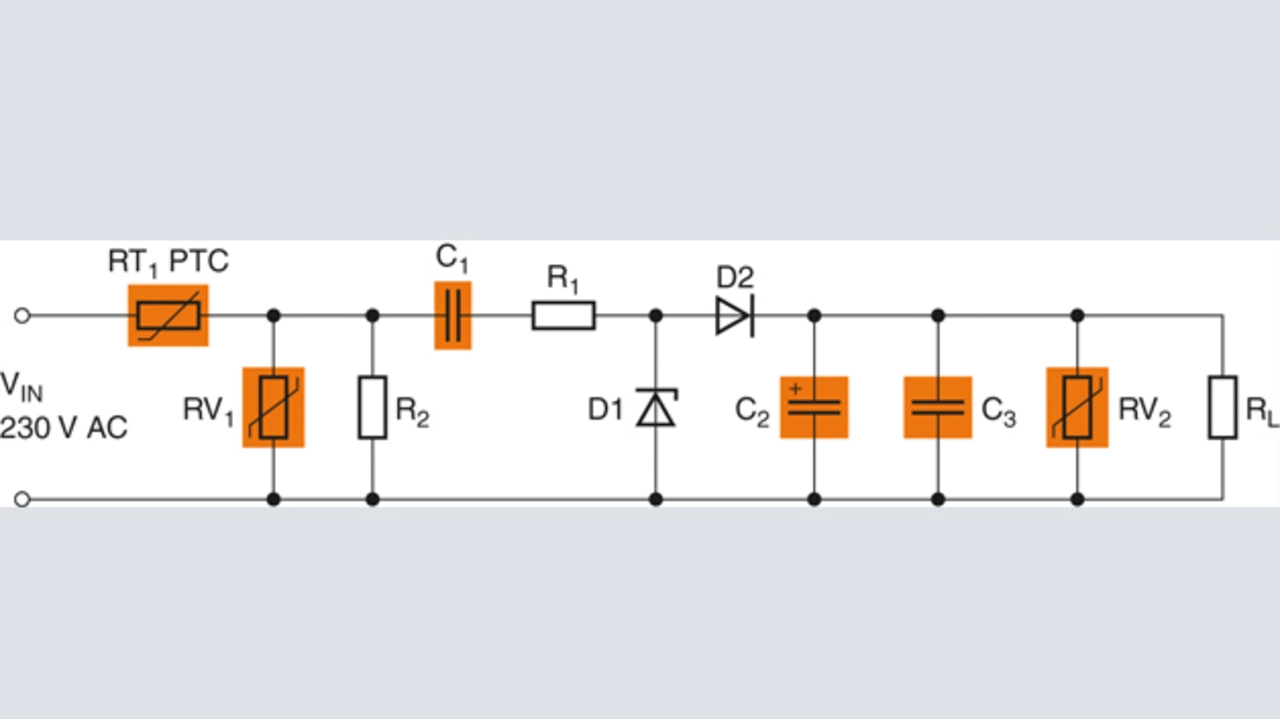
Meist werden Stromversorgungen benötigt, die am Ausgang eine Gleichspannung zur Verfügung stellen. Die einfachste Lösung besteht in der einpulsigen Gleichrichtung (Bild 2); für das Berechnungsbeispiel soll eine Ausgangsspannung von rund 9 V bei einem maximalen Laststrom von 15 mA erzeugt werden.

Zur Funktion der Zenerdiode D1: Während der positiven Halbwelle arbeitet D1 als spannungsbegrenzendes Bauelement. Um die Ausgangsspannung von 9 V zu erreichen, müsste die Zenerspannung bei 9,7 V liegen, weil an der Diode D2 rund 0,7 V abfallen. Da Zenerdioden mit diesem Wert aber nicht verfügbar sind, wird eine Diode mit 10 V und einer zulässigen Verlustleitung von 1,3 W gewählt. Wird die Stromversorgung im Scheitelpunkt der Netzspannung eingeschaltet, würde ein zu hoher Strom durch D1 fließen. Er wird mit R₁ begrenzt. Zenerdioden mit einer Verlustleistung von 1,3 W können in der Regel kurzfristige Ströme von etwa 1 A bewältigen. So lässt sich der Wert von R₁ nach Gleichung (1) berechnen. Der nächstgelegene Normwert ist 330 Ω.

(1) $R subscript 1 space equals space fraction numerator square root of 2 space times space U over denominator I subscript m a x end subscript end fraction space equals space fraction numerator square root of 2 space times space 230 space V over denominator 1 space A end fraction space equals space 325 comma 27 space Ω space$

R₁ musst im Betrieb den gesamten Laststrom tragen. Zur Berechnung ist das Verhältnis vom Effektivwert des Wechselstroms und zum Mittelwert des Gleichstroms zu berücksichtigen. Da es sich um eine einpulsige Gleichrichtung handelt, liegt der Formfaktor bei 2,22. Mit dem Ausgangsstrom von 15 mA ergibt sich somit ein Strom durch R1 von 33,3 mA und in der Folge eine Verlustleistung, die sich aus Gleichung (2) ergibt.

(2) $P space equals space I squared space times space R space equals space open parentheses 33 comma 3 space m A close parentheses squared space times space 330 space Ω space equals space 0 comma 366 space W$

Gewählt wird ein Widerstand mit einer Belastbarkeit von 0,5 W. Der Spannungsabfall über dem Widerstand beträgt knapp 11 V.

Aus den bisher ermittelten Daten lässt sich nun der erforderliche Blindwiderstand des Kondensators C₁ bestimmen. Um eine Versorgung der Last auch bei Unterspannung sicherzustellen, sollte die Berechnung mit einem Spannungsabfall der Netzspannung von mindestens 10 Prozent durchgeführt werden, außerdem ist der Spannungsabfall über R₁ und D1 zu berücksichtigen. So ergibt sich der Blindwiderstand aus Gleichung (3).

(3) $X subscript C 1 end subscript space equals space U subscript C 1 end subscript over I subscript m a x end subscript space equals space fraction numerator 230 space V space minus space 23 space V space minus 11 space V space minus 10 space V over denominator 33 comma 3 space m A end fraction space equals space 5585 comma 6 space Ω$

Daraus lässt sich bei der Netzfrequenz von 50 Hz nach Gleichung (4) die erforderliche Kapazität berechnen.

(4) $C subscript 1 space equals space fraction numerator 1 over denominator 2 straight pi space times space straight f space times space straight X subscript straight C 1 end subscript end fraction space equals space fraction numerator 1 over denominator 2 straight pi space times space 50 space Hz space times space 55 comma 85 comma 6 space Ω end fraction space equals space 0 comma 57 space mu F$