Advertorial
Exakte Bestimmung von Spulenverlusten mit RedExpert
Ein erheblicher Teil der Verluste in Schaltnetzteilen entsteht in Kern und Wicklungen von Speicherinduktivitäten. Ein besonders genaues Wechselstromverlustmodell in der Online-Design-Plattform RedExpert liefert zuverlässige Simulationsergebnisse.
In einem Schaltnetzteil (SMPS) besteht der größte Teil der Leistungsverluste in Form von Schalt- und magnetischen Verlusten, die durch den Kern und die Wicklungen in der Speicher-/Koppelspule entstehen. In der Vergangenheit wurden die Kernverluste anhand der Steinmetz-Gleichung und ihrer Erweiterungen berechnet. Diese Gleichungen können die Verluste nur für bestimmte Bedingungen oder Materialien zuverlässig abschätzen. Würth Elektronik hat daher ein eigenes Modell entwickelt, um die Kernverluste effektiv und genau zu bestimmen, das in der eigenen Online-Design Plattform RedExpert implementiert ist.
Energiespeicherung in Spule
In Schaltnetzteilen dient die Speicherdrossel als Speicherkomponente: Sie speichert Energie in Form eines Magnetfeldes während der Einschaltphase des Schaltreglers und gibt diese Energie während der Ausschaltphase an die Last ab. Die Speicherdrossel besteht üblicherweise aus einer mit Kupferdraht gefertigten Spule und einem Kern mit magnetischen Eigenschaften. Aus der elektromagnetischen Physik ist bekannt, dass, wenn eine magnetomotorische Kraft an eine Spule angelegt wird, diese im zeitlichen Verlauf einen Magnetfluss ø(t) induziert. An jeder Stelle ist die Magnetflussdichte B stets proportional zur Feldstärke H (Gleichung 1).
B ist die magnetische Flussdichte (ø/A), µr ist die Permeabilität des Materials, µ0 die Permeabilität der Luft und H die magnetische Feldstärke.
Die Spule ist wahlweise um den Kern gewickelt oder darin untergebracht. Der Kern enthält einen Luftspalt, um das magnetische Feld effektiv zu nutzen. Der Kern ist in der Regel aus Ferritmaterial mit ferromagnetischen Eigenschaften und einer sehr viel höheren Permeabilität als Luft. Aus der Reihenschaltung des hohen Luftspaltwiderstands mit dem widerstandsarmen Ferritmaterial, wird der Großteil der Energie im Luftspalt gespeichert.
Spulen unterliegen dem ampèreschen sowie dem faradayschen Gesetz. Das ampèresche Gesetz setzt den Strom in der Spule oder den Drahtwicklungen zum Magnetfeld im Spulenkern ins Verhältnis. Zur Annäherung wird angenommen, dass das Magnetfeld im Drosselkern über die gesamte Kernlänge (le) gleichförmig ist. Aufgrund dieser Annahme lässt sich das ampèresche Gesetz formulieren (Gleichung 2):
Hierbei ist N die Anzahl der Wicklungen der Spule um den Drosselkern und I der Spulenstrom.
Nach dem faradayschen Gesetz beträgt die an der Spule angelegte Spannung (Gleichung 3):
Aus den obigen Gleichungen lässt sich der Spulenwert berechnen (Gleichung 4):
Hierbei ist AC die Querschnittsfläche des Kerns.
Da Ferritmaterialien eine hohe Permeabilität aufweisen, stellen sie aufgrund des niedrigen magnetischen Widerstands einen einfachen Weg für den Magnetfluss dar. Diese Eigenschaft unterstützt den Fluss im Drosselkern, was die Konstruktion von Drosseln mit hohen Induktivitätswerten bei geringen Abmessungen ermöglicht. Dieser Vorteil ist aus Gleichung 4 klar ersichtlich: Ein Kernmaterial mit hoher Permeabilität ermöglicht eine kleinere Querschnittsfläche.
Bei Schaltnetzteilen lässt sich die maximale Magnetflussdichte gemäß Gleichung 5 berechnen:
Auch gekoppelte Drosseln (Sperrwandler-Übertrager) sind Spulen, nur mit mehreren Wicklungen. Diese Wicklungen sind komplexer zu betrachten, aber die Kerneigenschaften bleiben hiervon unberührt.
Leistungsverluste treten bei Spulen in den Wicklungen und im Kern auf und heißen folglich Wicklungs- bzw. Kernverluste.
Wicklungsverluste
Die Leistungsverluste in den Wicklungen entstehen aufgrund des Gleichstromwiderstands (RDC) der Wicklungen, des Skin-Effekts und des Proximity-Effekts. Leistungsverluste aufgrund des Gleichstromwiderstands lassen sich mit der folgenden Gleichung 6 näherungsweise bestimmen:
P = I2 ⋅ RDC (6)
Die durch den Skin- und den Proximity-Effekt bedingten Leistungsverluste werden als Wechselstromwiderstand (RAC) der Wicklung bezeichnet, der in erster Linie von der Frequenz abhängt. Es gibt einige Methoden zur Ermittlung dieser Effekte in magnetischen Bauteilen, doch sind zur näherungsweisen Bestimmung dieser Verluste komplizierte Berechnungen wie bei der Dowell-Methode nötig.
Kernverluste
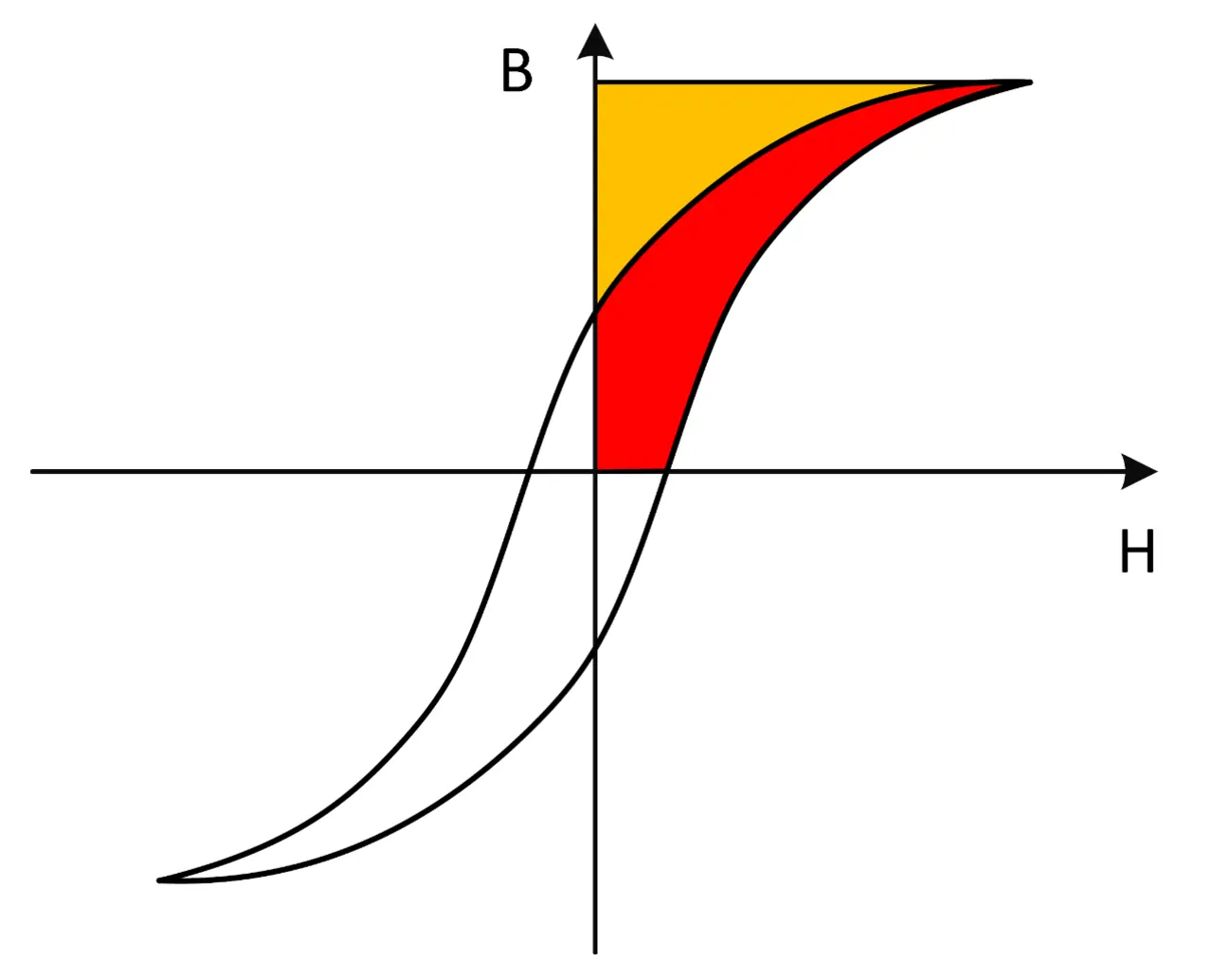
Zur Bestimmung der Kernverluste lässt sich B in Abhängigkeit von H messen. Die Ansprechcharakteristik von B zu H ist nicht linear und zeigt eine Hysterese (daher die Bezeichnung Hysteresekurve). Die Hysterese stellt die Eigenschaften des Kernmaterials dar, die zum Leistungsverlust im Spulenkern führen. Bild 1 zeigt eine typische BH-Kurve bei sinusförmiger Anregung des Kerns.
Der Energieverlust eines Schaltzyklus im Kern entspricht der Differenz zwischen der Magnetenergie, die dem Kern während der Einschaltphase zugeführt wird, und der Magnetenergie, die während der Ausschaltphase aus dem Kern abgezogen wird. Dies wird verursacht durch die Elementarmagnete, die in der Ausschaltphase nicht von alleine in die Ausgangslage zurückfallen, sondern mit Energieaufwand zurückgestellt werden müssen.
Unter Verwendung des ampèreschen und des faradayschen Gesetzes lässt sich die Energie im Kern gemäß Gleichung 7 ausdrücken:
Der Energieverlust im Kern ist der von der BH-Kurve umschlossene Bereich multipliziert mit dem Kernvolumen. Der Leistungsverlust entspricht dem Produkt aus diesem Energiewert (E) und der Schaltfrequenz.
Dieser Ausdruck ist unter den Bedingungen gültig, dass der Kern nicht in die Sättigung gefahren wird und die Schaltfrequenz im vorgesehenen (linearen) Betriebsbereich liegt. Der Bereich der Hysteresekurve (in Bild 1 rot gekennzeichnet) stellt den Energieverlust dar. Der Leistungsverlust hängt davon ab, wie häufig pro Sekunde die Hysteresekurve durchlaufen wird. Insofern stehen die Hystereseverluste in direktem Zusammenhang mit der Frequenz.
Die zweite Form der Kernverluste entstehen durch Wirbelströme, die durch einen zeitlich veränderlichen Fluss dø/dt im Kernmaterial induziert werden. Nach der Lenz‘schen Regel wird durch eine Änderung eines Magnetflusses ein Strom induziert, der seinerseits einen Magnetfluss induziert, der dem ursprünglichen Fluss entgegenwirkt. Dieser Wirbelstrom fließt durch das leitfähige Kernmaterial und erzeugt I²R-Verluste.
Exaktes Wechselstromverlustmodell
Anfänglich wurden Kernverluste mithilfe der Gleichung 8 ermittelt, die auch als Steinmetz-Gleichung bekannt ist.
Hierbei sind Pv die Kernverluste (bedingt durch Hysterese und Wirbelströme) je Volumeneinheit, f die Frequenz, Bpk die höchste Flussdichte einer sinusförmigen Anregung und K, α und β Konstanten, die aus einem Kernverlustdiagramm abgeleitet werden. Der wesentliche Nachteil der Steinmetzgleichung besteht darin, dass sie vor allem für sinusförmige Anregungen gilt. Diesen Nachteil sollte die Entwicklung der modifizierten und der generalisierten Steinmetz-Gleichung [1] ausgleichen, was aber nur sehr eingeschränkt gelang.
Würth Elektronik eiSos hat daher ein hochmodernes Modell entwickelt, mit dem Kunden die passende Induktivität mit hoher Effektivität auswählen, und ihre Schaltung optimieren können. Dieses Modell basiert auf den empirischen Daten, die mit einem Echtzeitanwendungsaufbau gewonnen werden.
Beim Modell von Würth Elektronik eiSos werden die Gesamtverluste der Induktivität in Wechselstrom- und Gleichstromverluste unterteilt. Die Leistungsverluste aufgrund des Gleichstroms in den Spulenwicklungen werden als Gleichstromverluste, die Leistungsverluste infolge der magnetischen Aussteuerung in der Spule und im Kern als Wechselstromverluste bezeichnet.
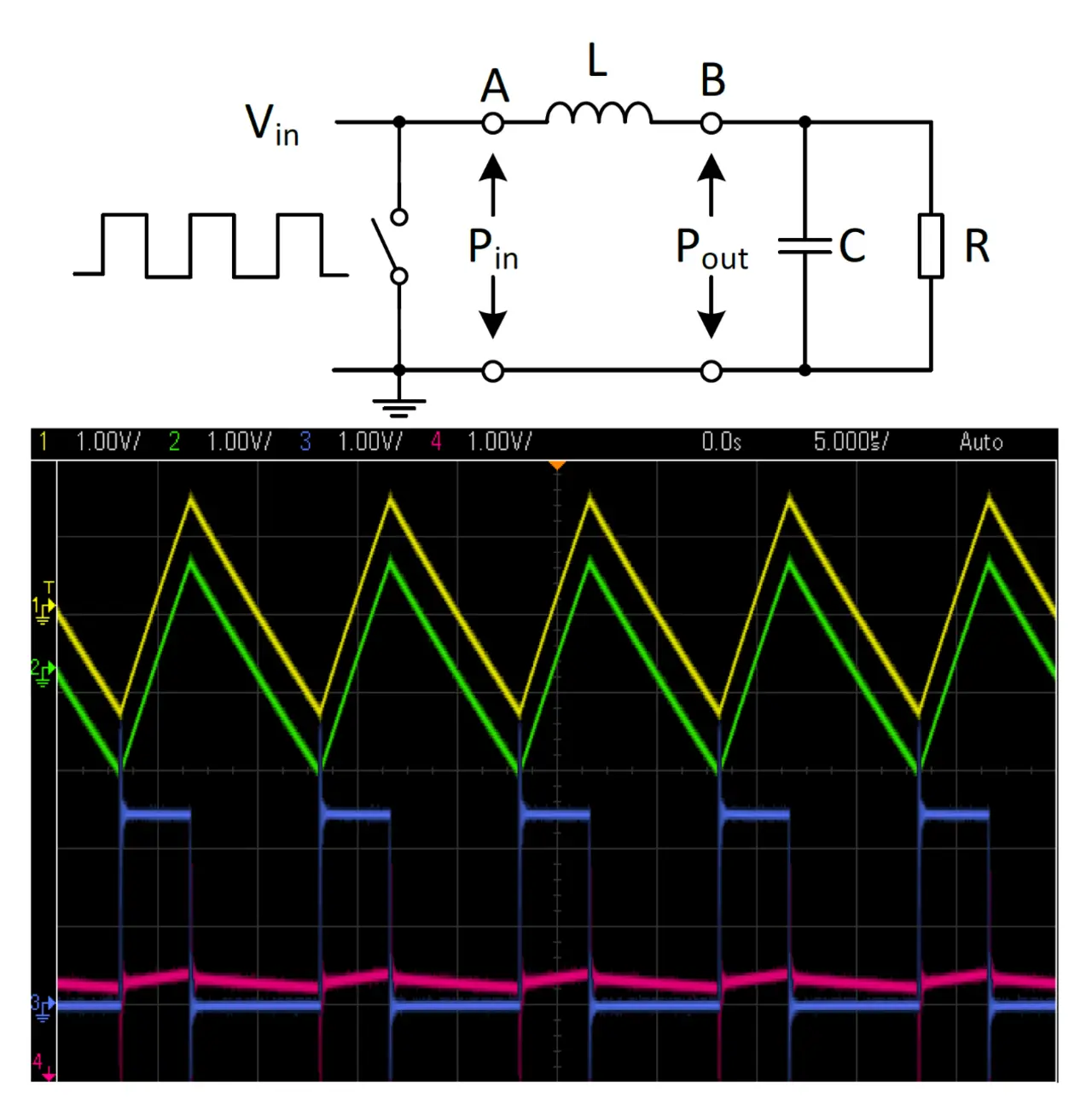
Empirische Daten werden mit einem DC/DC-Wandler erfasst, wie er in Bild 2 gezeigt ist. An die Induktivität wird eine pulsierende Spannung angelegt, dann werden die Eingangsleistung Pin und die Ausgangsleistung Pout gemessen. Auf dieser Basis wird PLoss = Pin - Pout geschätzt und die Wechselstromverluste der Spule PAC werden separiert. Dieser Vorgang wird für unterschiedlichste Parametereinstellungen – beispielsweise Schwankungen der magnetischen Aussteuerung, Frequenz, Rippelstrom, usw. – gemessen, um so die empirischen Daten aufzeichnen zu können. Mithilfe dieser empirischen Daten wird das Modell zur Berechnung der Wechselstromverluste erstellt: PAC = f(∆I, freq, DC, k1, k2).
Die in den Datenblättern für typische Kernmaterialien gezeigte Hysteresekurven stellen die magnetische Aussteuerung von + nach – des Kerns durch ein sinusförmiges Signal dar. Die Hysteresekurve gibt dabei den in Bild 3 oben dargestellten Energieverlust an.
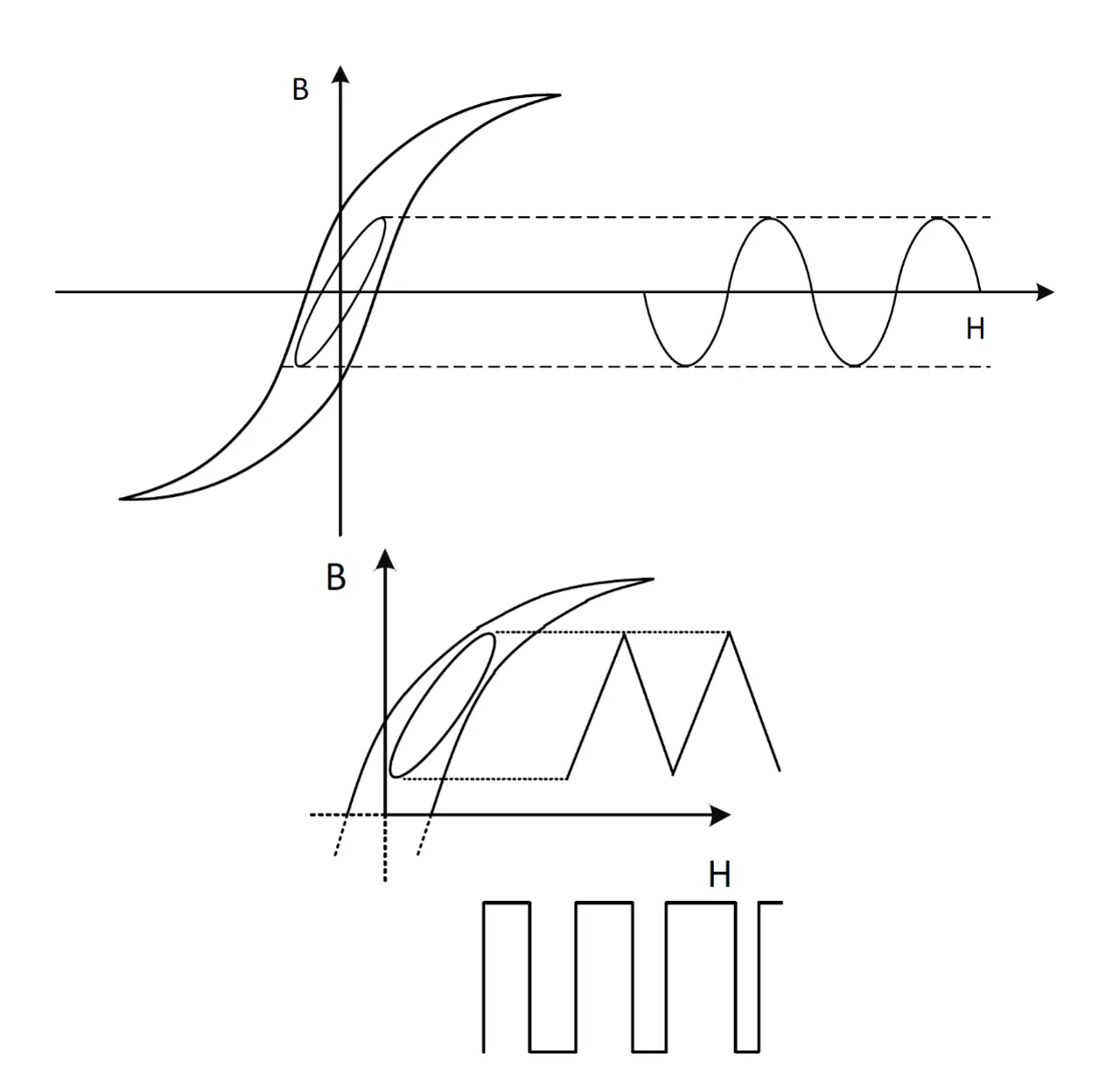
Bei einer Schaltnetzteilanwendung wird der Kern normalerweise durch eine wesentlich kleinere Rechteckwellenform mit einer maximalen Flussdichte betrieben, die durch die Kernverluste auf eine kleinere Hysteresekurve beschränkt wird (Bild 3 unten). Der Leistungsverlust hängt davon ab, wie häufig pro Sekunde die Hystereseschleife durchlaufen wird. Insofern stehen die Hystereseverluste in direkter Abhängigkeit zur Frequenz. Die Hysteresekurve ändert ihre Form bei Änderungen der Signalform, des Antriebsstroms bzw. der Antriebsspannung und der Temperatur. Diese Schwankungen machen eine genaue Vorhersage der Kernverluste ausgesprochen schwierig. Die kleinere Hysteresekurve hängt von der Spannung über der Drossel ab. Diese kleinere Hysteresekurve wird genau am Arbeitspunkt zur Erzeugung empirischer Daten für das Wechselstromverlustmodell von Würth Elektronik verwendet. Es hat sich als robust und präzise für weite Bereiche von Parametern wie Frequenz, Rippelstrom und Tastverhältnis erwiesen.
Vorteile des AC-Verlustmodells von Würth Elektronik:
- Da die empirischen Daten ausschließlich auf Echtzeitparametern basieren, lässt sich eine genaue Ermittlung der Verluste für jedes gegebene Tastverhältnis erzielen.
- Das Modell funktioniert über einen weiten Frequenzbereich (10 kHz - 10 MHz) sehr genau, da die Konstanten der Leistungsgleichung über einen weiten Bereich ermittelt wurden, unter Einbeziehung der magnetischen Aussteuerung.
- Sogar geringfügige Änderungen im Kernmaterial und der Wicklungsstruktur werden berücksichtigt.
- Ist gültig für Bauteile aus mehr als einem Material.
- Gestattet exakte Ermittlung von Verlusten bei Eisenpulver und neuen „Metal Alloy“ Materialien.
- Gültig für beliebige Kernformen und Windungsstrukturen.
- Umfasst AC-Wicklungsverluste.
Das Modell von Würth Elektronik wurde ausgiebig validiert und mit bestehenden Modellen und gemessenen Daten verglichen. Wechselstromverluste für verschiedene Materialien wie WE-Superflux, Eisenpulver, NiZn, MnZn usw. werden über große Tastverhältnis- und Frequenzbereiche gemessen und mit theoretischen Modellen verglichen [1].
Leistungsverluste mit RedExpert bestimmen
Mit der Online-Design-Plattform RedExpert gibt Würth Elektronik den Kunden ein Werkzeug zur Bauteileauswahl und -simulation an die Hand, mit dem sich unkompliziert eine für die jeweilige Anwendung geeignete Speicherdrossel auswählen lässt.
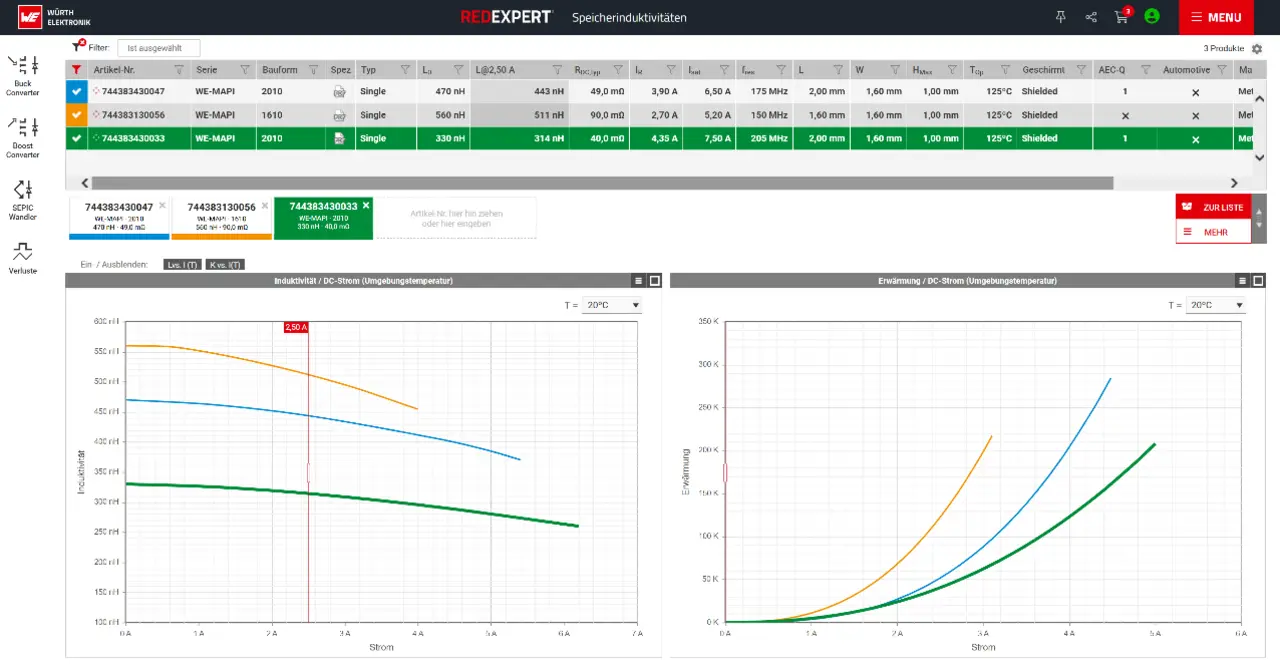
Zunächst gibt der Benutzer die Eingangs- und Ausgangsparameter in die gewünschte Topologie ein. Dann berechnet RedExpert den Induktivitätswert und zeigt die passenden Induktivitäten an (Bild 4). Da Würth Elektronik eiSos eine sehr umfangreiche Palette von Speicherdrosseln für alle möglichen Einsatzzwecke anbietet, sollte jeder Benutzer nach Eingabe der Parameter ein für seine Zwecke geeignetes Bauteil finden. Die Berechnung der AC-Verluste in einem magnetischen Bauteil ist ebenso kritisch wie komplex, nicht jedoch mit RedExpert, da das neue AC-Verlustmodell von Würth Elektronik in das Tool integriert ist. Aufgrund der genauen Berechnung der kompletten AC-Verluste eignet sich die Anwendung auch zur Temperaturabschätzung.
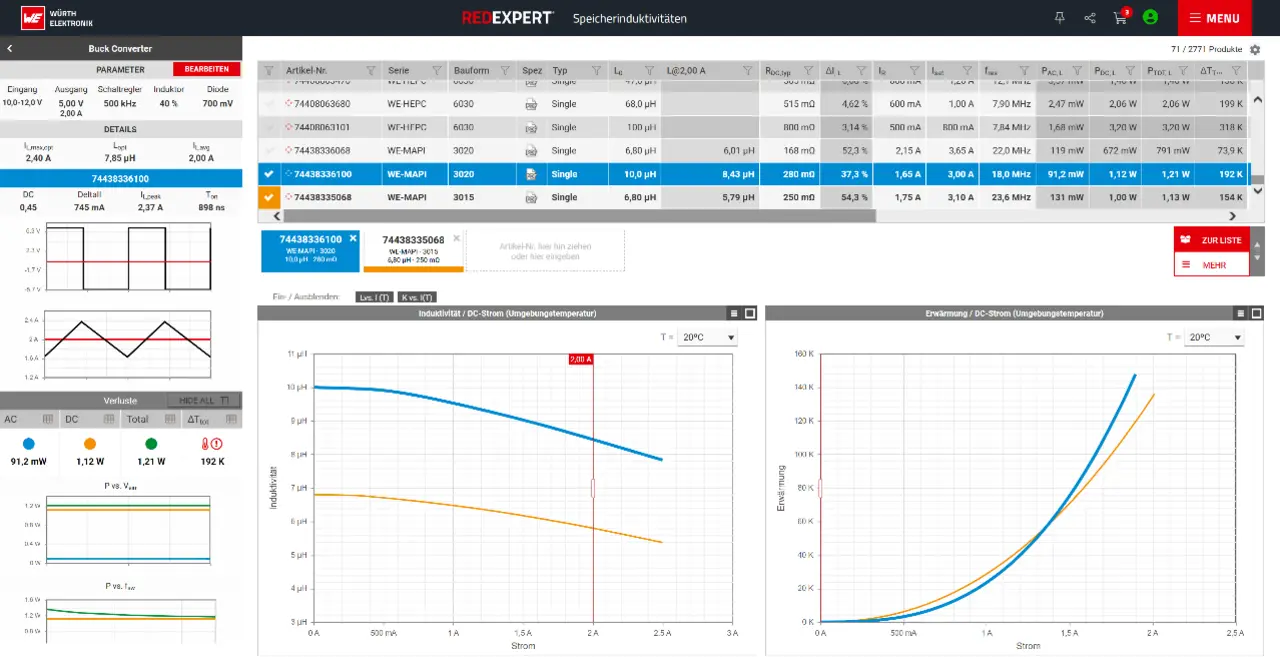
Bild 5 zeigt ein Beispiel. Hier wurde ein Tiefsetzsteller (buck converter) ausgewählt. Als Eingangsspannung werden 10 - 12 V angegeben, als Ausgangsspannung 5 V, Schaltfrequenz 500 kHz, ein Rippelstrom der Induktivität von 40 % und als Ausgangsstrom 2 A. Für diese Werte hat RedExpert eine optimale Induktivität (Lopt) von 7,85 µH, eine Einschaltdauer von 898 ns und ein Tastverhältnis von 0,45 berechnet. Für dieses Beispiel werden mehr als 200 Produkte zur Auswahl vorgeschlagen. Geht man in diesem Beispiel davon aus, dass für die Anwendung eine sehr kleine und verlustarme Speicherdrossel benötigt wird, so fällt die Entscheidung auf ein Exemplar aus der WE-MAPI-Baureihe.
Autor
Ranjith Bramanpalli schloss 2008 sein Studium an der University of Massachusetts in Lowell mit Mastern in Elektrotechnik und Informatik ab. Seither arbeitete er im Bereich Leistungselektronik, wobei sein Schwerpunkt auf Forschung, Entwicklung und Anwendung liegt. Zurzeit ist er als Product Application Engineer bei Würth Elektronik eiSos tätig.
[1] Application Note ANP029: Exakte Bestimmung von Spulenverlusten mit RedExpert; www.we-online.de/ANP029





