Wege zur THD-Wert-Optimierung:
Verzerren für bessere Messungen
Fortsetzung des Artikels von Teil 2
Praktisches Experiment mit digitaler Vorverzerrung
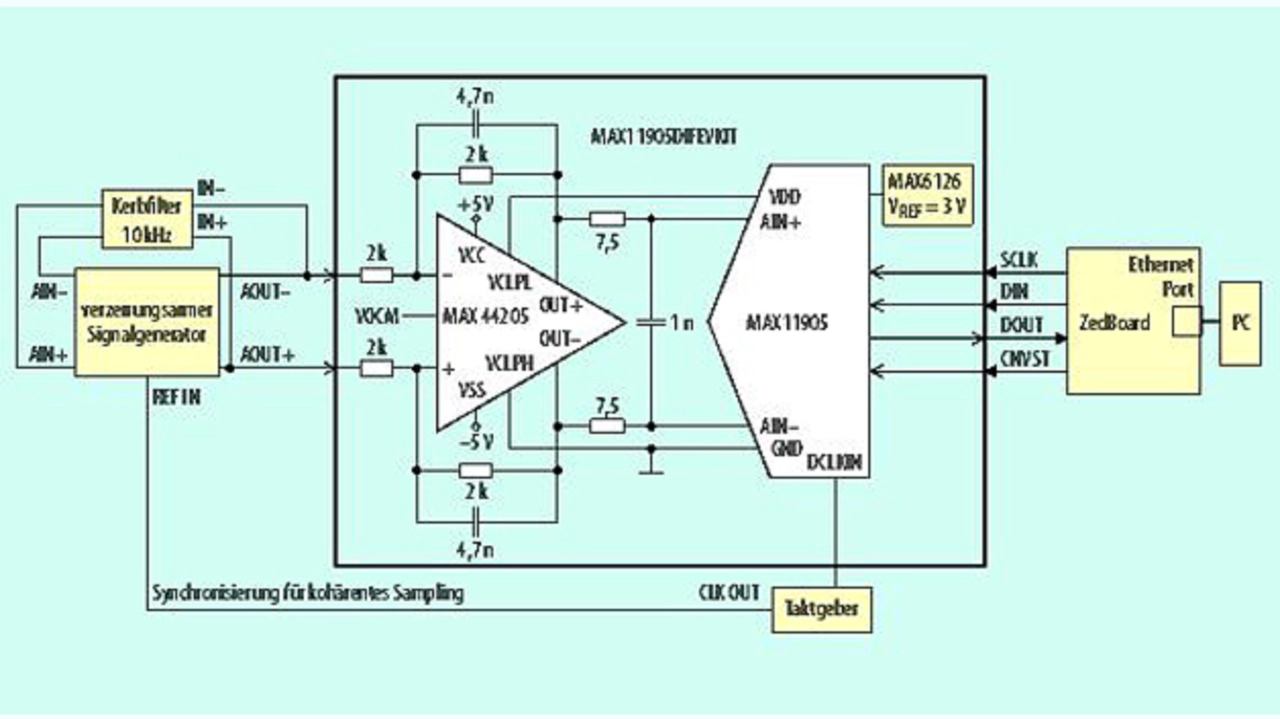
Mit einem Arbitrary-Waveform-Generator und dem Prüfaufbau aus Bild 4 wurde eine 10-kHz-Sinuswelle erzeugt. Der Spektrumanalysator misst dabei die Verzerrung des Signalgenerators. Mit einem 10-kHz-Kerbfilter wird die Grundschwingung abgeschwächt, um die Verzerrungen des Spektrumanalysators zu reduzieren.
Bild 5 zeigt das Spektrum der erzeugten Sinuswelle nach dem Kerbfilter und ohne digitale Vorverzerrung. Die Grundschwingung bei 10 kHz hat –23 dBV, die Oberschwingung zweiter Ordnung –112 dBV und die Oberschwingung dritter Ordnung –117 dBV. Bild 6 gibt die Verhältnisse nach dem Kerbfilter wieder, wenn die digitalen Codes, die in den internen Pufferspeicher des Signalgenerators geladen wurden, einer digitalen Vorverzerrung unterzogen wurden.
Jobangebote+ passend zum Thema
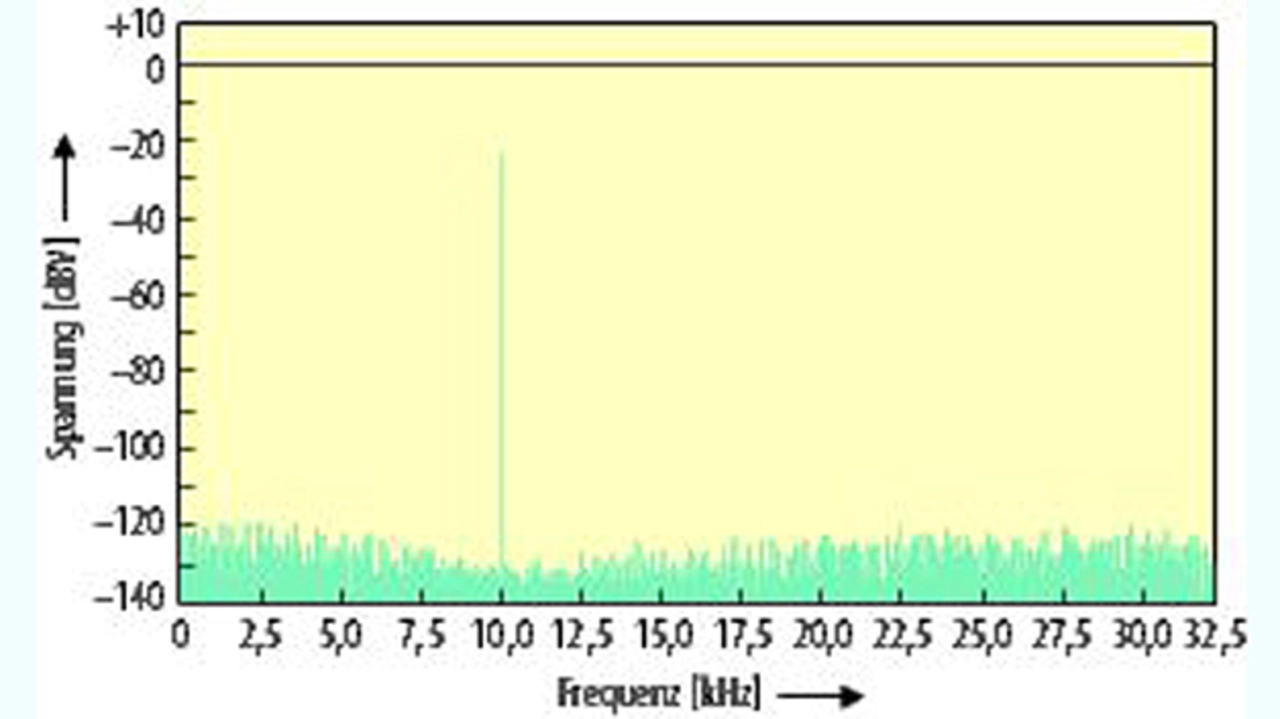
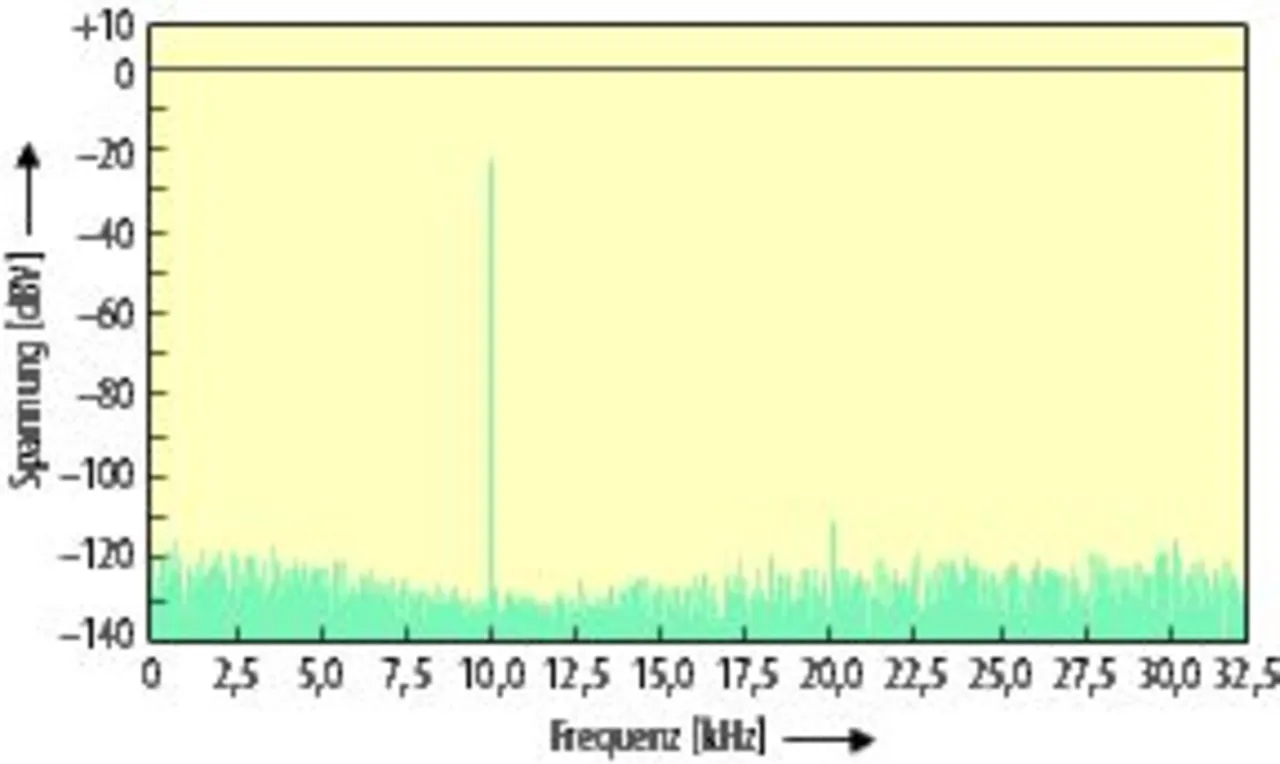
Im Anschluss an die digitale Vorverzerrung hat sich die Oberschwingung zweiter Ordnung von –112 dBV auf –123 dBV reduziert und die Oberschwingung dritter Ordnung von –117 dBV auf –124 dBV. Dies trägt zur Verbesserung des THD-Werts bei.
Bei dieser Methode zur digitalen Vorverzerrung sollte man mit großer Sorgfalt vorgehen und eine Oberschwingung nach der anderen reduzieren. Hierzu werden alle mit der dritten Oberschwingung im Zusammenhang stehenden Parameter auf null gesetzt, während man die zweite Oberschwingung gemäß Gleichung 3 abschwächt. Aus Bild 5 ist zu entnehmen, dass die zweite Oberschwingung im FFT-Plot mit ca. –112 dB angegeben ist, was 2,5 µV entspricht. Iterativ werden für A2 Werte zwischen –2,5 µV und +2,5 µV eingesetzt, um herauszufinden, welcher Wert die zweite Oberschwingung am besten vermindert. Nach wenigen Iterationen stellt sich heraus, dass dies mit A2 = –1,5 µV am besten gelingt. Mit dem Parameter φ2 wird nun die Oberschwingung weiter abgeschwächt. A2 = –1,5 µV kombiniert mit φ2 = –45° erzielt, wie Bild 6 zeigt, die besten Ergebnisse zur Eliminierung der zweiten Oberschwingung. Nach demselben iterativen Verfahren erhält man für die dritte Oberschwingung A3 = –0,5 µV in Verbindung mit φ3 = 45° (siehe auch hierzu Bild 6).
DAS-Messung mit DPD am Signalgenerator
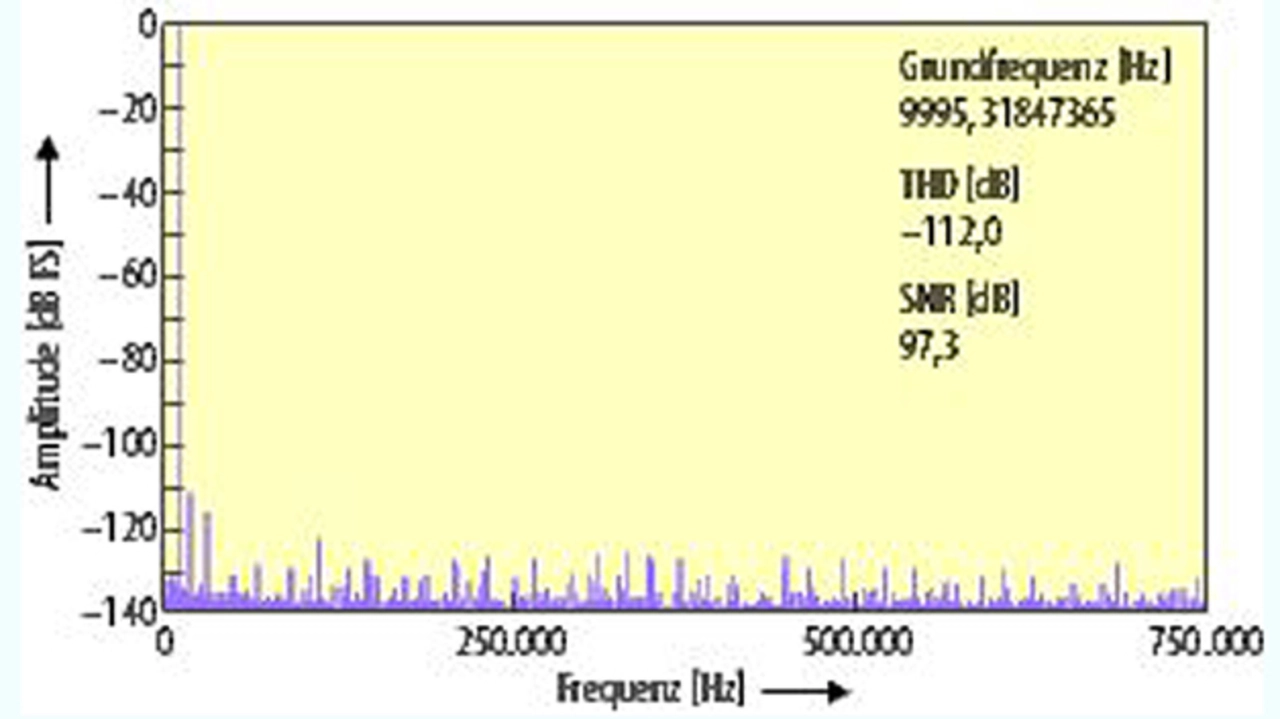
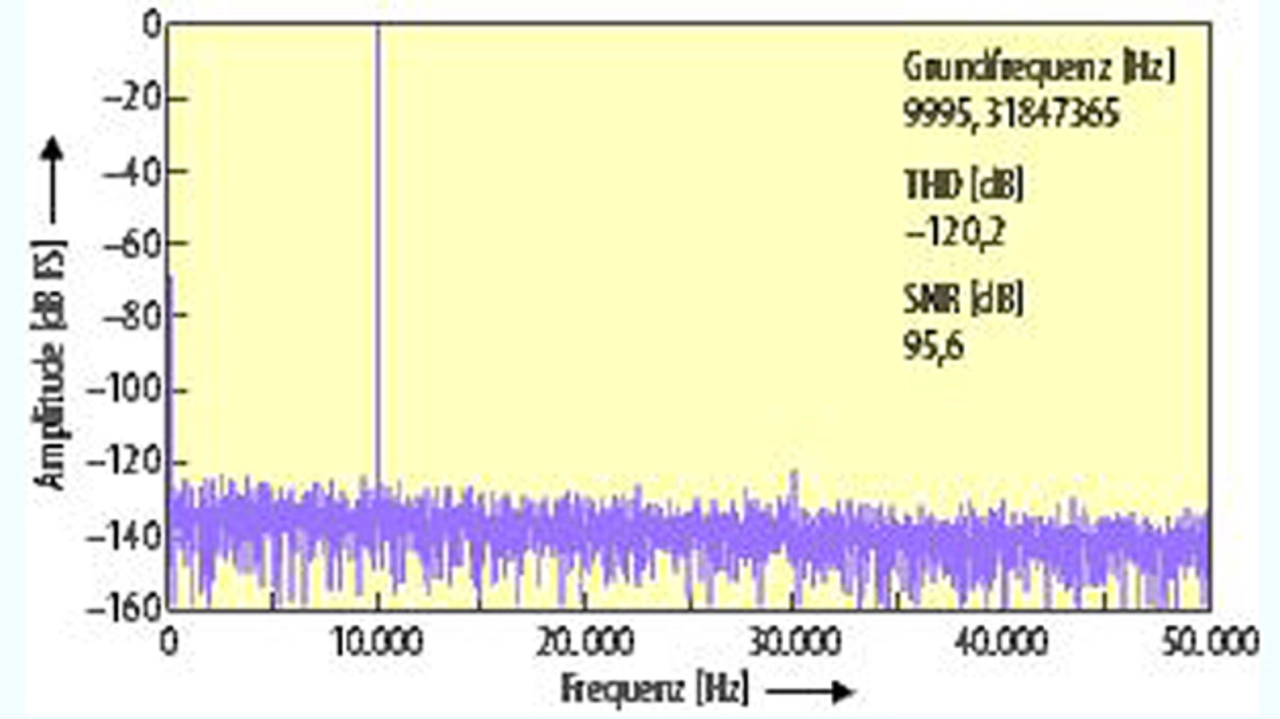
Bild 7 gibt die Performance des DAS bei 1,6 MS/s nach Eliminierung der zweiten und dritten Oberschwingung wieder.
Die dynamischen Eigenschaften des MAX11905DIFFEVKIT in der Betriebsart Arb Wfm(D/A) mit digitaler Vorverzerrung verbesserte den gemessenen THD-Wert des DAS um 8 dB, nämlich von –112 dB auf –120 dB (bei 1,6 MS/s).
Einschränkung des SNR durch den Arbitrary-Waveform-Modus
Die Oberschwingungen in der Betriebsart Arb Wfm(D/A) werden mit der digitalen Vorverzerrung eliminiert. Allerdings ist im Arbitrary-Waveform-Modus eine Verschlechterung des SNR gegenüber der Betriebsart Sine(D/A) zu beobachten.
Bild 8 zeigt das Verhalten des DAS bei 1,6 MS/s in der Betriebsart Sine(D/A) des Signalgenerators. Die Daten machen deutlich, dass sich der SNR hier gegenüber dem Arbitrary-Waveform-Modus um 2 dB verbessert. Das Phänomen, dass der SNR in der Betriebsart Arb Wfm(D/A) schlechter ist als in der Betriebsart Sine(D/A), bedarf einer genaueren Untersuchung.
Die Autoren:
| Srudeep Patil |
|---|
| ist seit Juli 2011 bei Maxim Integrated als Applications Engineer tätig und beschäftigt sich hauptsächlich mit Operationsverstärkern, Komparatoren, Strommessverstärkern, ADCs und Spannungsreferenzen. Patil besitzt ein Master-Diplom in Elektrotechnik mit dem Schwerpunkt Analog/HF VLSI. Vor seinem Wechsel zu Maxim hatte er eine Praktikantenstelle bei NXP Semiconductors inne und war dort im Analog-Team auf den Gebieten ADCs und Verstärker tätig. |
| Carmelo Morello |
|---|
| arbeitet als Senior Business Manager in der Industrial and Healthcare Business Unit von Maxim Integrated und ist dort für die geschäftlichen Aktivitäten auf dem Industrie- und Telekommunikationsmarkt zuständig. Bis zu seinem Eintritt bei Maxim war Morello als Analog Field Application Engineer und R&D Designer für präzise und schnelle Signalketten-Schaltungen bei bekannten internationalen Unternehmen beschäftigt. An der Universität Pavia (Italien) erwarb Morello ein Master-Diplom in Elektrotechnik. |
- Verzerren für bessere Messungen
- DAS-Messungen auf traditionelle Art
- Praktisches Experiment mit digitaler Vorverzerrung
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Erste Universität in Europa nutzt Watson
Mit Twitter-Daten Grippewelle vorhersagen
Maxim Integrated Products
IO-Link-Transceiver senkt Verluste um 50 Prozent
Arbitärgeneratoren
Gute Dynamik bei bis zu 1,25 GSa/s
Oszilloskop, Analysator, Signalgenerator
Von Kickstarter zum Open Source Messgerät
