Wege zur THD-Wert-Optimierung:
Verzerren für bessere Messungen
Fortsetzung des Artikels von Teil 1
DAS-Messungen auf traditionelle Art
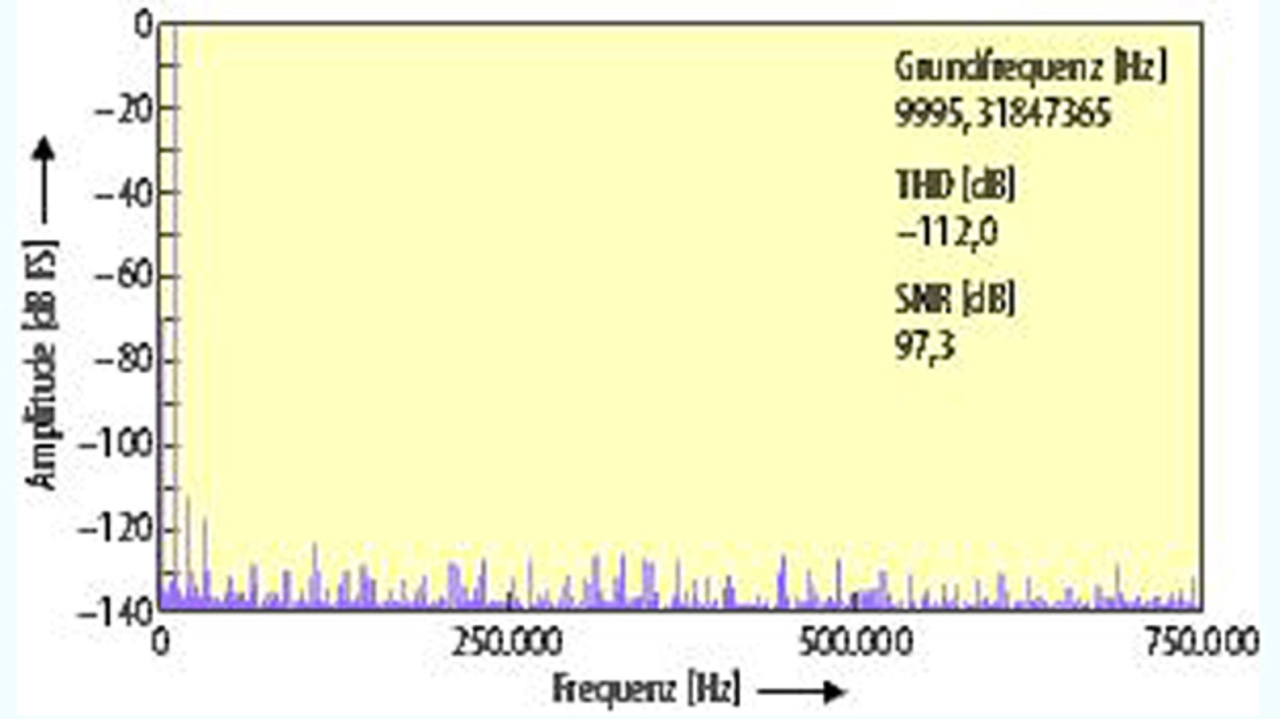
Die in Bild 2 gezeigten Ergebnisse geben die dynamischen Eigenschaften des DAS wieder – gemessen mit dem in Bild 1 gezeigten Prüfaufbau. Der ADU läuft dabei mit einer Abtastrate von 1,6 MS/s.
Ein SNR von 97,3 dB ist als relativ gut anzusehen, doch der Oberschwingungsgehalt des Ausgangssignals ist größer, als man es für das DAS erwartet hätte. Wie im Folgenden erläutert wird, ist der gemessene THD-Wert infolge der Verzerrungen des Signalgenerators auf –112 dB beschränkt.
Bessere Verzerrungswerte durch digitale Vorverzerrung
Um die Verzerrungen bzw. den THD-Wert des digitalen Signalgenerators zu verbessern, wird eine digitale Korrekturtechnik angewandt. Das gezielte Hinzufügen von Oberschwingungen zu einem digitalen Signal mit der Absicht, die von der Digital-Analog-Umsetzung hervorgerufenen Oberschwingungen zu reduzieren oder ganz zu eliminieren, wird als digitale Vorverzerrung (englisch: Digital Predistortion, DPD) bzw. als digitale Linearisierung bezeichnet. Die Blockschaltung in Bild 3 gibt eine Übersicht über die Haupt-Baugruppen eines typischen digitalen Signalgenerators.
Jobangebote+ passend zum Thema
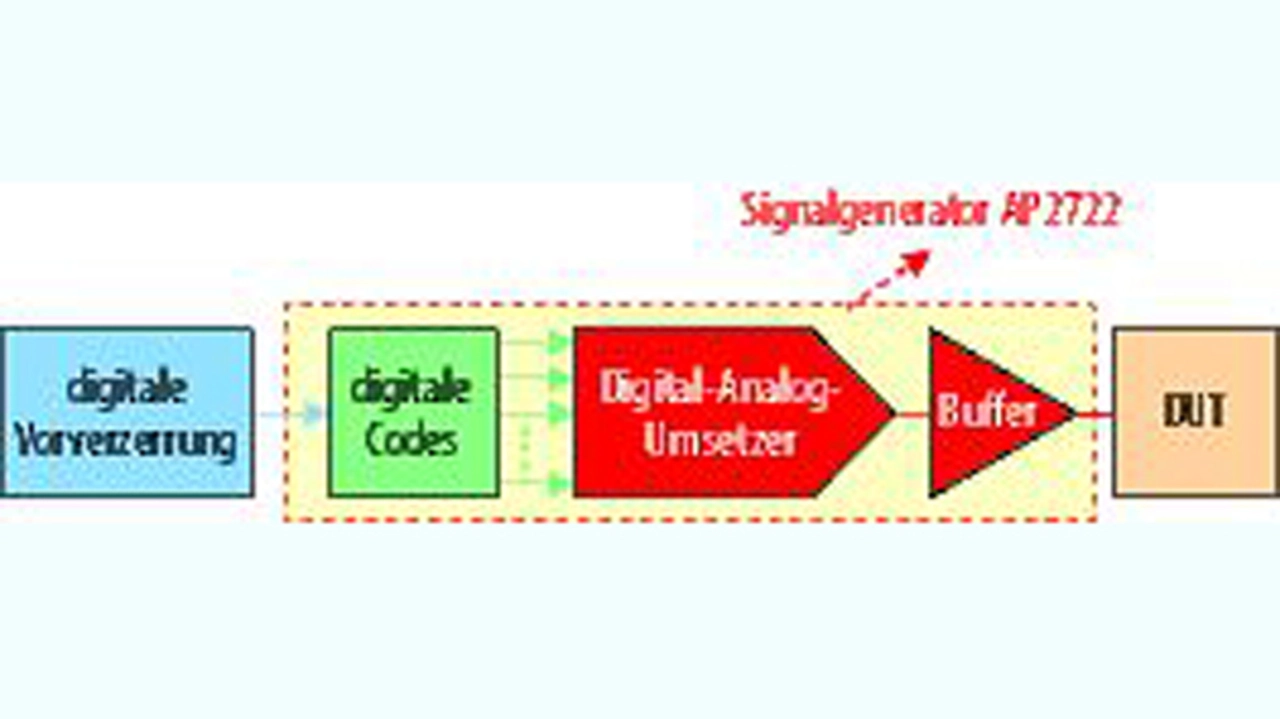
Die folgende Aufstellung skizziert die Funktionsweise:
- Der mit „Digital Codes“ bezeichnete Teil speichert die digitalen Codes des Signalverlaufs.
- Der DAU-Block wandelt die digitalen Codes in die entsprechenden analogen Werte um.
- Der Buffer-Teil stellt die nötige Leistung und die passende Ausgangsimpedanz zum Ansteuern des Prüflings bereit.
- Der mit ‚digitale Vorverzerrung‘ bezeichnete Abschnitt stellt die verzerrte Wellenform zur Verfügung.
Beim Signal zum Ansteuern des Prüflings handelt es sich um eine Sinuswelle, die der Signalgenerator aus digitalen Codes erzeugt.
Gleichung 1 gibt die digitalen Codes der Sinuswelle wieder, die dem DAU zur Erzeugung des analogen Ausgangssignals zugeführt werden. (Die Farben der Gleichungen 1, 2, 3, 4 und 5 entsprechen den Farben der verschiedenen Abschnitte in Bild 3.)
yd steht in der Gleichung für das digitale Signal, A1 ist die Amplitude der Grundschwingung, ω1 = 2πf1, f1 ist die Frequenz der Sinus-Grundschwingung, t ist die Abtastperiode und φ1 ist die Phase der Grundschwingung.
Gleichung 2 gibt das analoge Ausgangssignal des Signalgenerators an. Darin stehen die roten Terme für die Oberschwingungen zweiter und dritter Ordnung, die durch den DAU und den Puffer entstehen.
A2 und A3 sind die Amplituden der Oberschwingungen zweiter bzw. dritter Ordnung, φ2 und φ3 die entsprechenden Phasen.
In Bild 3 fügt der blau dargestellte Digitale-Vorverzerrungs-Block gegenphasige Oberschwingungen mit gleicher Amplitude hinzu, um die Oberschwingungen am Ausgang des Signalgenerators zu eliminieren. In Gleichung 3 steht ydDPD steht für die digital vorverzerrte Wellenform. 
Das in Gleichung 3 generierte Signal wird an den DAU gerichtet (siehe Bild 3). Das neue Signal am Ausgang des Signalgenerators lautet demnach:
yaDPD ist hierin das mit digitaler Vorverzerrung versehene analoge Ausgangssignal.
Die gleich- und gegenphasigen Terme der Oberschwingungen zweiter und dritter Ordnung heben sich gegenseitig auf, sodass Gleichung 5 entsteht:
Die Auswahl der Oberschwingungen zweiter und dritter Ordnung für das digital vorverzerrte Signal ist das Resultat eines später in diesem Beitrag genauer erläuterten iterativen Prozesses.
Implementierung der digitalen Vorverzerrung
In diesem Experiment wurde der digitale Signalgenerator AP2722 in zwei Betriebsarten eingesetzt:
- In der Betriebsart Sine(D/A) (Sinuswelle)
- In der Betriebsart Arb Wfm(D/A) (Arbitrary Waveform)
Die Betriebsart Sine(D/A) wurde für die in den Bildern 2 und 8 gezeigten Messungen verwendet, die Betriebsart Arb Wfm(D/A) dagegen für die Messungen, deren Ergebnisse in den Bildern 5, 6 und 7 zu sehen sind.
In den Messungen für Bild 2 erzeugt der Signalgenerator ein 10-kHz-Sinussignal zum Evaluieren des DAS. Für die digitale Vorverzerrung wurde dagegen der Arbitrary-Waveform-Modus des Signalgenerators (Bild 3) gewählt. Die mit Hilfe von Matlab erzeugten digitalen Codes für eine 10-kHz-Sinuswelle sind in einer WAV-Datei abgelegt. Diese digitalen Codes lassen sich in den Signalgenerator laden und mit dessen integriertem D/A-Umsetzer in ein analoges Sinussignal mit 10 kHz verwandeln. Die maximale Kapazität des internen Puffers im Signalgenerator ermöglicht die Speicherung von 16.384 digitalen Codes.
- Verzerren für bessere Messungen
- DAS-Messungen auf traditionelle Art
- Praktisches Experiment mit digitaler Vorverzerrung
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Erste Universität in Europa nutzt Watson
Mit Twitter-Daten Grippewelle vorhersagen
Maxim Integrated Products
IO-Link-Transceiver senkt Verluste um 50 Prozent
Arbitärgeneratoren
Gute Dynamik bei bis zu 1,25 GSa/s
Oszilloskop, Analysator, Signalgenerator
Von Kickstarter zum Open Source Messgerät
