Digitale Filter
IIR-Filter in FPGAs implementieren - Teil 1
Fortsetzung des Artikels von Teil 1
Struktur der IIR-Filter
IIR-Filter-Struktur
Ein IIR-Filter besteht aus einem Vorwärts-FIR-Filter, auch bekannt als All-Zero-Filter, einschließlich des Zählers b (Koeffizienten für die Nullen) und einem Rückkoppel-FIR für den Nenner a (Koeffizienten für die Polstellen). Eine Art, einen IIR-Filter zu beschreiben, ist seine Z-Übertragungsfunktion mit Zähler-Koeffizienten bi und Nennerkoeffizienten ai:
Jobangebote+ passend zum Thema
Festkomma-Implementationen
Um einen zufriedenstellenden Festkomma-Betrieb des IIRFilters sicherzustellen, sind Untersuchungen hinsichtlich Koeffizientenquantifizierung, interner Quantifizierung, Überlauf und Stabilität notwendig.
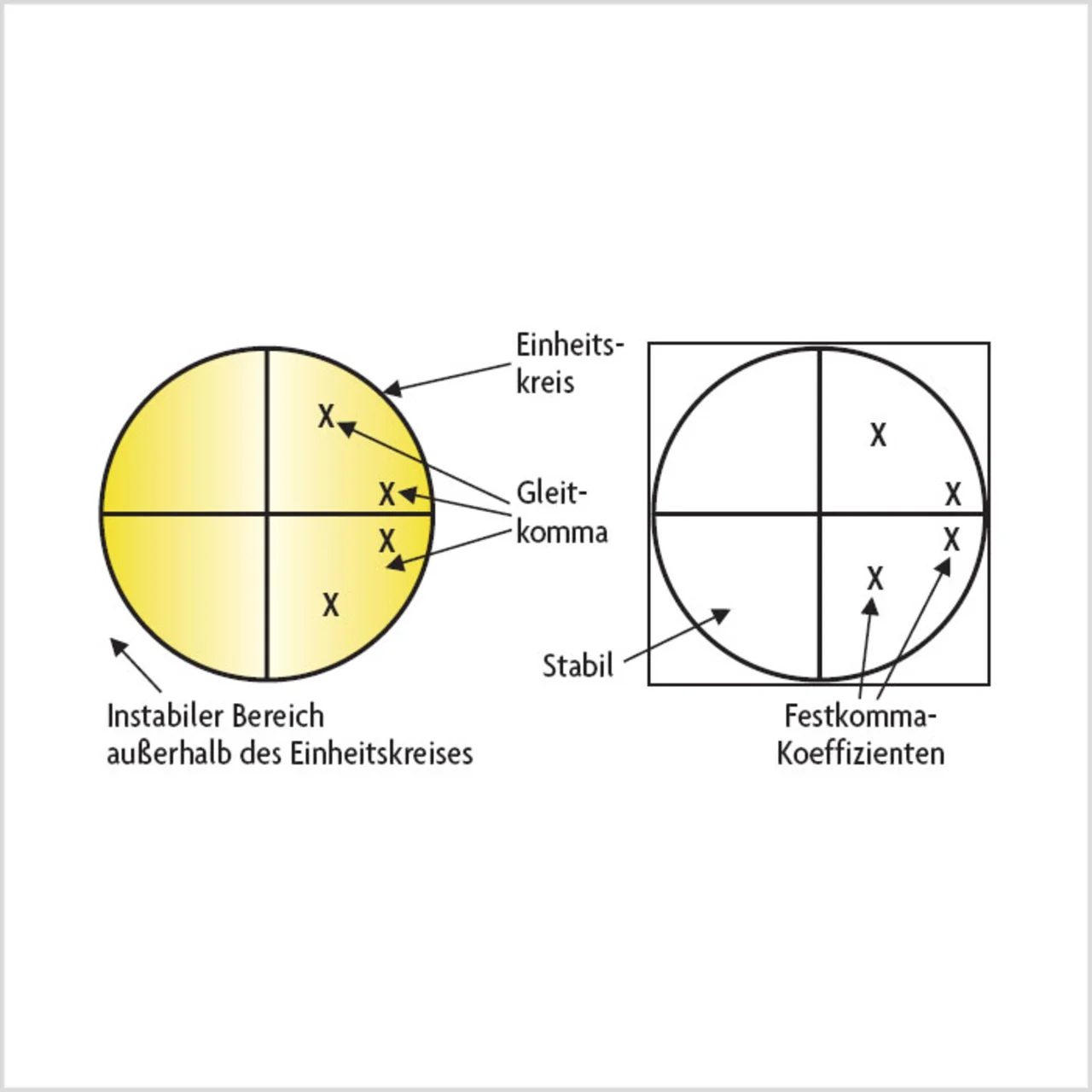
Die Koeffizientenquantifizierung beeinflusst den Frequenzgang. Um den Effekt der Quantifizierung zu erkennen, ist es sinnvoll, das Filter im Z-Bereich zu betrachten und die Pol-/Nullstellen-Darstellung zu verwenden. Diese zeigt, wie die Nullen und Pole (Spitzen im Frequenzgang) positioniert sind. Tatsächlich hat das Problem der IIR-Stabilität mit den Koeffizienten des Nenners und ihrer Position zu tun (Bild 5).
Die Pole für die Gleitkomma-Version sind in Bild 5 links dargestellt. Sie liegen innerhalb des Einheitskreises, was bedeutet, dass die Werte der Koeffizienten kleiner sind als 1 und deshalb in der stabilen Region liegen. Nachdem die Koeffizienten quantifiziert sind, verschieben sich diese Pole und wirken sich auf die Frequenzantwort aus. Wenn sie sich auf den Einheitskreis hin bewegen (die Pole sind gleich 1), wird das Filter definitiv instabil. Die Multiplizierer in den Spartan-3- und Virtex-4-FPGA-Familien erlauben Koeffizienten bis zu 18 bit für vorzeichenlose Werte und bis zu 25 bit im XtremeDSP-Slice in den Virtex-5-FPGAs. Die Flexibilität der FPGA-Architektur ermöglicht es, noch größere Multiplizierer zu realisieren, um die Auswirkungen der Koeffizientenquantifizierung zu reduzieren.
In einer DSP-Funktion sind stets Multiplikationen sowie Addition und Subtraktion enthalten. Es gibt jedoch ein „Bit-Wachstum“ aufgrund dieser Funktionen, und ab einem bestimmten Punkt muss die Wortbreite reduziert werden. Deshalb müssen für die LSBs (Least Signifikant Bit) Funktionen wie Runden/Abschneiden eingesetzt werden. Die Rundung reduziert die Bitbreite, ist aber eine Rauschquelle und steuert zum Rauschen am Ausgang bei und wirkt sich deshalb auf das Signal-Rausch-Verhältnis (SNR) aus. Die Flexibilität der FPGA-Architektur erlaubt eine größere Wortlänge und reduziert damit das Rundungsrauschen. Deshalb ermöglicht die Verwendung der Xtreme-DSP-Slices bis zu 40 bit in den Spartan-3A-DSP-FPGAs und bis 48 bit in den Virtex-4- und Virtex-5-FPGAs. Es können sogar noch größere Wortbreiten durch die Kaskadierung von XtremeDSP-Slices erzeugt werden.
Für eine Festkomma-Implementierung gibt es eine feste Bitbreite und deshalb einen bestimmten Bereich. Als ein Ergebnis der Berechnungen kann das Filter seinen Maximal-/Minimal-Bereich überschreiten. Der Wert eines Zweierkomplements von 01111000 (+120) + 00001001 (+9) ist 10000001 (–127). Die großen positiven Zahlen werden in eine große negative Zahl überführt. Dieser Effekt ist als „Wraparound“ bekannt und kann große Fehler verursachen. Der Einsatz von Sättigungslogik kann diese Situation mildern. In diesem Beispiel wäre das Ergebnis 01111111 (+127). Um die Auswirkung einer Bereichsüberschreitung zu minimieren, lässt sich die Skalierung verwenden. Damit können Werte nicht mehr überlaufen. Es gibt verschiedene Arten der Skalierung, und diese werden häufig von DSPs benutzt, da sie gut in ihre feste Struktur passen. Dies hat jedoch wiederum einen Effekt auf das Signal-Rausch-Verhältnis.
Betrachtet man nur den Rückkopplungspfad des rekursiven Filters, ist dies grundsätzlich ein Polynom höherer Ordnung:
Das MathWork-Tool liefert mathematische Funktionen wie die Wurzelberechnung, um zu helfen, diese Gleichung zu lösen, die Lösungen mit doppelter Genauigkeit zu bestimmen und den Betrag auszugeben. Dabei ist leicht festzustellen, ob ein Wert größer als 1 ist und damit Instabilität anzeigt. Es wird ebenfalls die Anzahl der Pole angezeigt, die nahe am Einheitskreis liegen, und somit wird hervorgehoben, welche Koeffizienten besondere Beachtung benötigen und welche mehr Bits für die Genauigkeit erfordern.
Koeffizientenwerte von IIR-Filtern höherer Ordnung
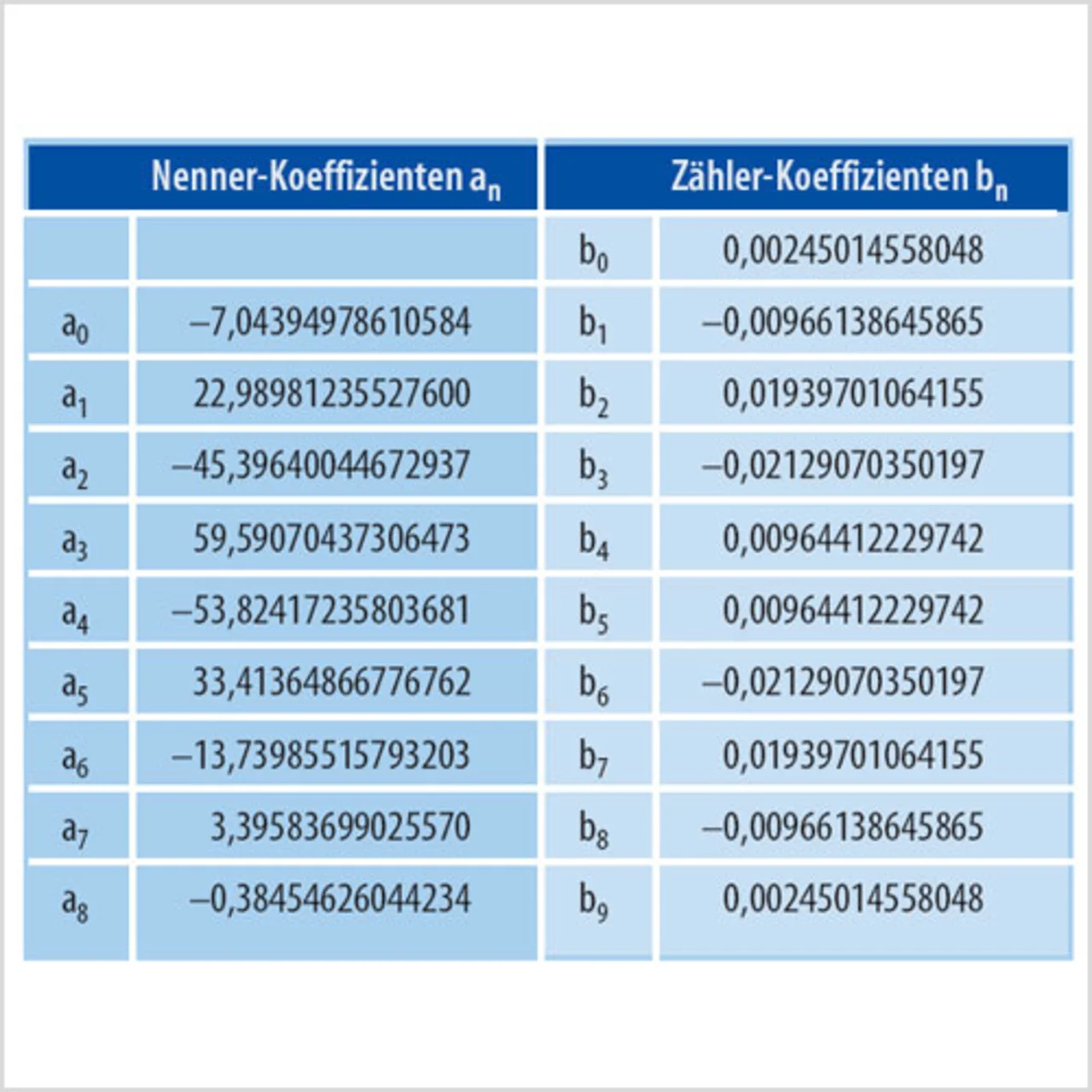
In Tabelle 1 sind die Koeffizienten für die 9. direkte Form der verwendeten IIR-Filterspezifikationen aufgelistet. Obwohl dies ein Filter 9. Ordnung ist, hat es tatsächlich 19 Koeffizienten: zehn für den Zähler und neun für den Nenner. Dies stellt eine Design-Herausforderung dar, da die Koeffizienten des Zählers fraktioniert sind, die Nennerkoeffizienten hingegen einen Ganzzahlenbereich haben und deshalb auch eine hohe Genauigkeit. Deswegen erfordern beide Koeffizientensätze eine Festkomma-Repräsentation mit adäquatem Bereich und Genauigkeit. Die Zählerkoeffizienten sind in diesem Falle jedoch symmetrisch und könnten deshalb vorteilhaft in FPGAs implementiert werden.
Für die Zählerkoeffizienten verbessert ein Erhöhen der Bitbreite den Frequenzgang nicht. Da das Filter aber die eingebetteten Multiplizierer in der FPGA-Schaltmatrix benutzt, wird eine Multiplizierer-Bitbreite von 18 bit empfohlen. Um jedoch noch eine weitere Verbesserung zu erzielen, können mehr als 18 bit notwendig sein. Eine Untersuchung der binären Repräsentation der Koeffizienten kann dabei helfen. Der Koeffizientenwert 0,00245014558048 resultiert bei 17 bit Genauigkeit in dem Zweierkomplement 000000000101000001. Damit die eingebetteten Multiplizierer nicht Zeit damit verschwenden müssen, alle diese Nullen zwischen dem binären Punkt und der ersten aktiven 1 zu multiplizieren, wird empfohlen, die Zählerkoeffizienten mit 2 zu potenzieren und die resultierenden Produkte mit dem gleichen 2er-Potenzwert herunterzuskalieren.
18 bit für den Nennerkoeffizienten a3 benötigen 7 bit zur Darstellung der Ganzzahl, wodurch nur mehr 11 bit für die Genauigkeit übrig bleiben, was zu Instabilität führen kann. Eine Möglichkeit ist es, die Bitbreite zu erhöhen, aber das würde zu 25 × 18 Multiplikationen führen, was zwar akzeptabel für den DSP48E ist, aber zwei Hardware-Multiplizierer in den anderen FPGA-Familien benötigt. Weiterhin ist 59,59070437306473 = 64 – 4,40929562693527, und 4,40929562693527 kann durch FIX_ 18_14 repräsentiert werden, d.h. ein 18-bit-Wert mit 14 bit zum Richtigstellen des Binärpunktes. Die Multiplikation mit 64 ist nichts weiter als eine Verschiebung, die via Verdrahtungs-Routing im FPGA implementiert wird.
Direkt-Form-Strukturen
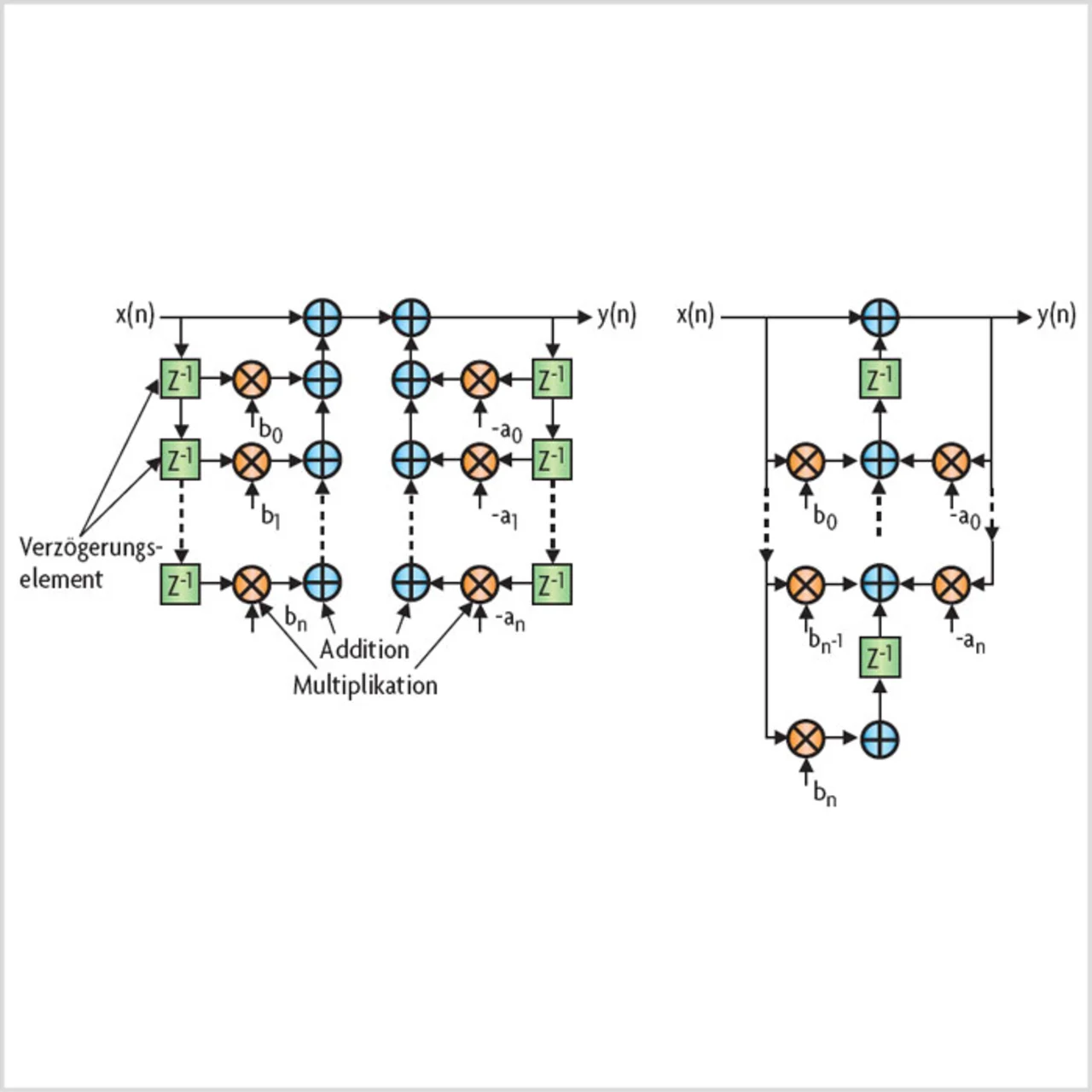
Die Direkt-Form-I-Struktur lässt sich als zwei FIR-Filter betrachten: ein aus den b-Koeffizienten bestehendes Vorwärts-FIR-Filter und ein reverses FIRFilter, das die a-Koeffizienten nutzt. Die IIR-Struktur kann in einer anderen Form neu geordnet werden (Bild 6). Die transponierte Direkt-Form-IStruktur ist in diesem Bild rechts dargestellt. Sie hat einen zentralen Zweig, bestehend aus Verzögerungselementen und Addierern. Es gibt zwei Multiplizier-Sektionen für die Zähler- und die Nennerkoeffizienten, die diesen Zweig speisen.
In der transponierten IIR-Struktur wird das Vorwärtsfilter vom All-Pol-Filter gefolgt. Deshalb wird das Signal gedämpft, bevor es an die höhere Verstärkung des All-Pol-Filters gelangt. Das Vorwärtsfilter ist durch die Bitbreite des Dateneingangs definiert.
Beim Vorwärtsfilter gibt es höhere Verzögerungen wegen der Verwendung von Pipeline-Registern. Die All-Pol-Sektion ist wegen der Rückkopplung der begrenzende Faktor und läuft langsamer. Da aber höhere Taktraten in einem FPGA möglich sind, sind Multizyklen für die Implementierung des Vorwärtsfilters verfügbar. Das Vorwärtsfilter kann unter Einsatz des CORE-Generator-FIR-Compilers implementiert werden, der den gleichen Grad an Abstraktion bietet, d.h. bis herunter zur Entwicklung auf der untersten Ebene, aber er bietet Zugriff auf die maximale Leistung, die im FPGA vorhanden ist. Für das All-Pol-Filter können die Daten- und Koeffizientenbreite größer sein, erfordern dann aber auch größere Multiplizierer.
Bei der Direkt-Form-I-Architektur können die Vorwärts- und reversen Filterstufen ausgetauscht werden. Wenn dies erfolgt, dann besteht das Zentrum aus zwei Spalten mit Verzögerungselementen. Dies kann in eine einspaltige Struktur umgewandelt werden, bekannt als kanonisch, was bedeutet, dass sie nur eine minimale Speicherkapazität benötigt. In diesem Fall kann verteilter Speicher, der innerhalb der FPGA-Schaltmatrix verfügbar ist, verwendet werden.
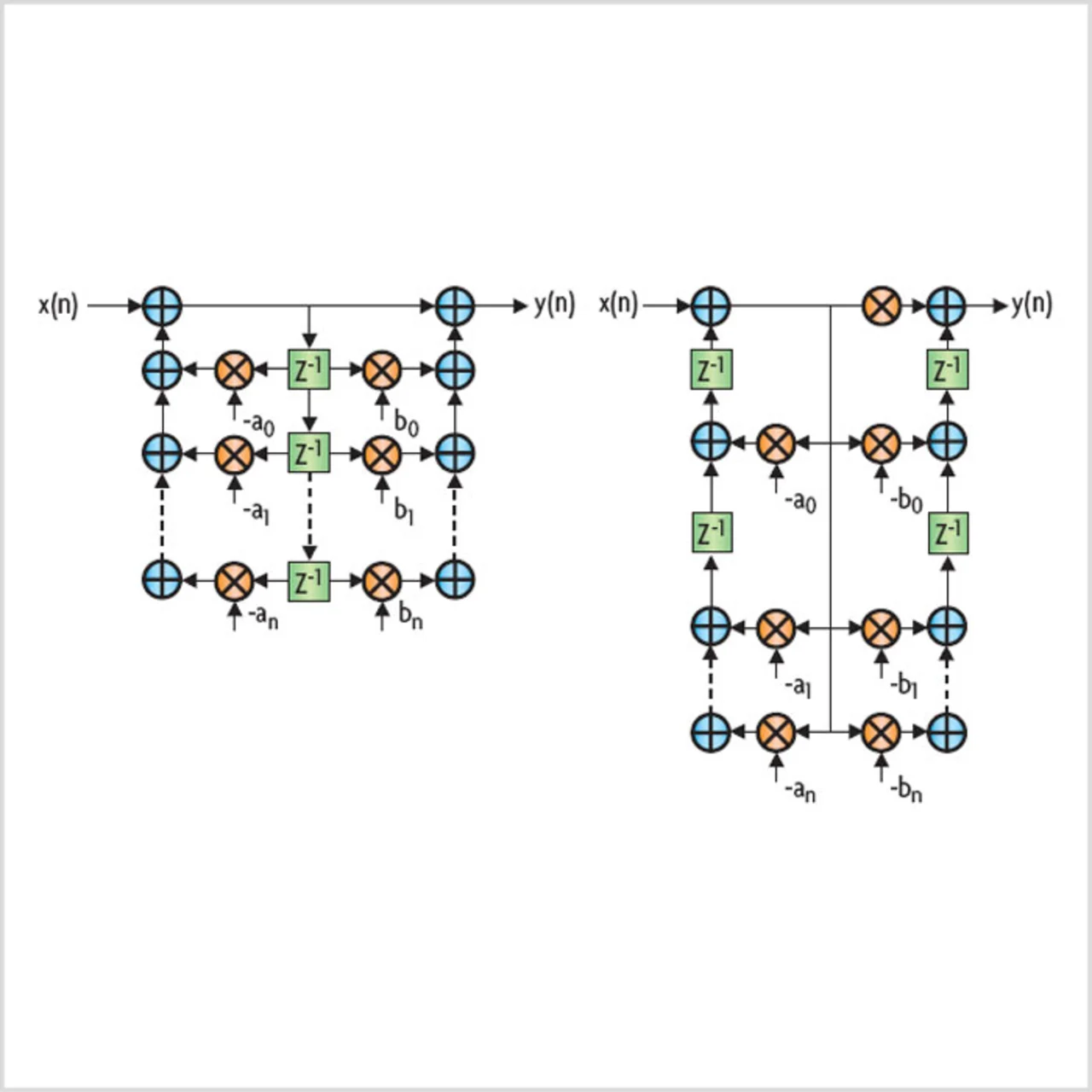
Die Direkt-Form-II-Struktur hat Vorteile gegenüber der Direkt-Form-I, da sie weniger Speicherplatz für die Datenwerte benötigt. Diese Filtertypen vereinen ein All-Pol-Filter, gefolgt von einem All-Zero-Vorwärts-Filter (Bild 7). Das Problem dabei ist die hohe Verstärkung der All-Pol-Sektion. Die Addierer sind größer, um einen potentiellen Überlauf zu handhaben. Der Vorteil des reduzierten Speicherbedarfs wird von den größeren Addierern wieder aufgehoben. Deshalb tendiert man bei dieser Struktur dazu, den Eingang zu skalieren, um die Verstärkung zu reduzieren, was aber zu einem schlechten Signal-Rausch-Verhältnis für Filter höherer Ordnung führen kann. Es ist deshalb das Beste, diese Struktur nicht für Filter größer als 2. Ordnung zu verwenden.
Literatur
[1] Loomis, H.H.; Sinha, B.: High Speed Recursive Digital Filter Realization Circuits. Circuits, Systems and Signalprocessing, 1984, Vol. 3, pp. 267 – 294, ISSN 0278-081X.
[2] Parhi, K.K.; Messerschmitt, D.G.: Pipeline Interleaving and Parallelism in Recursive Digital Filters. IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. 3, pp. 1099 – 1135, Juli 1989.
[3] Website von Xilinx: www.xilinx.com.
| B.Sc. Michael Francis |
|---|
| studierte an der Leicester Polytechnic (heute De Montfort University) in Großbritannien und schloss sein Studium mit einem B.Sc. ab. Bevor er im Jahr 2001 zu Xilinx wechselte, war er bei Firmen wie Racal und Newbridge Networks tätig. Sein Schwerpunkt liegt bei der digitalen Signalverarbeitung mit dem System Generator von Xilinx. Er entwickelt damit Lösungen für die Digitale Kommunikation, insbesondere Forward-Error-Correction-IP. |
Michael.Francis@xilinx.com
- IIR-Filter in FPGAs implementieren - Teil 1
- Struktur der IIR-Filter