Digitale Filter
IIR-Filter in FPGAs implementieren - Teil 1
Die Mehrzahl der digital implementierten Filter sind vom Typ FIR (Finite Impulse Response). Sie werden für einen großen Abtast-Bereich benutzt und im Hinblick auf Entwicklungswerkzeuge, Software und IP-Cores gut unterstützt. Das IIR-Filter (Infinite Impulse Response) wird bei geringeren Abtastraten unter 2000 kHz verwendet und nicht so gut von Entwicklungswerkzeugen unterstützt. Dieser zweiteilige Artikel beschreibt die unterschiedlichen Arten von IIR-Filtern und ihre Strukturen und zeigt unter Einsatz von Mathworks-Werkzeugen, wie diese Strukturen in die Architektur von Xilinx-FPGAs implementiert werden können und wie man IIR-Filter zusammenschalten kann, um höhere Abtastraten zu erzielen.
Das FIR-Filter nimmt abgetastete Signale auf, verarbeitet sie und gibt die verarbeiteten Signale aus. Die Vorteile des FIR-Filters sind, dass es einen stabilen linearen Phasengang hat, unempfindlich gegenüber Quantisierungseffekten ist, einfach zu entwickeln ist und nicht unter Problemen mit Grenzzyklen leidet.
Jobangebote+ passend zum Thema
Das IIR-Filter ist eine rekursive Filterstruktur, was bedeutet, dass die Ausgangssignale rückgekoppelt werden, um den nächsten Ausgang zu realisieren. IIR-Filter haben tendenziell einen besseren Amplitudengang, benötigen weniger Koeffizienten, erfordern weniger Speicherplatz für Variable, haben geringere Latenz und sind näher an den analogen Modellen.
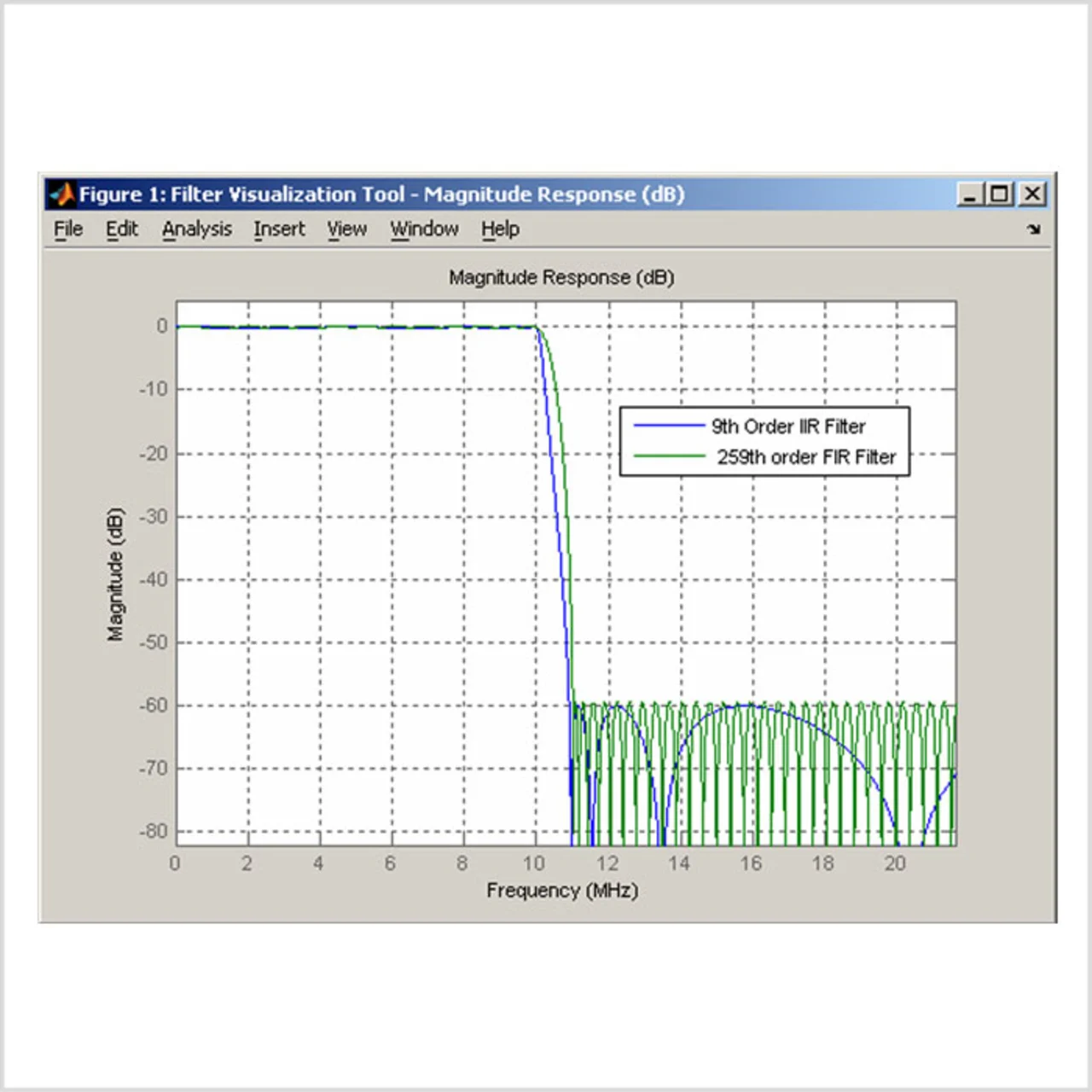
Bild 1 zeigt die Frequenzgänge eines FIR- und eines IIR-Filters. Man sieht, dass für eine Abtastrate von 100 MHz und eine Eckfrequenz von 10 MHz mit einer Stoppfrequenz von 11 MHz für die FIR-Filter-Implementierung ein Filter 259. Ordnung nötig ist. Für die gleichen Parameter reicht ein IIR-Filter 9. Ordnung aus.
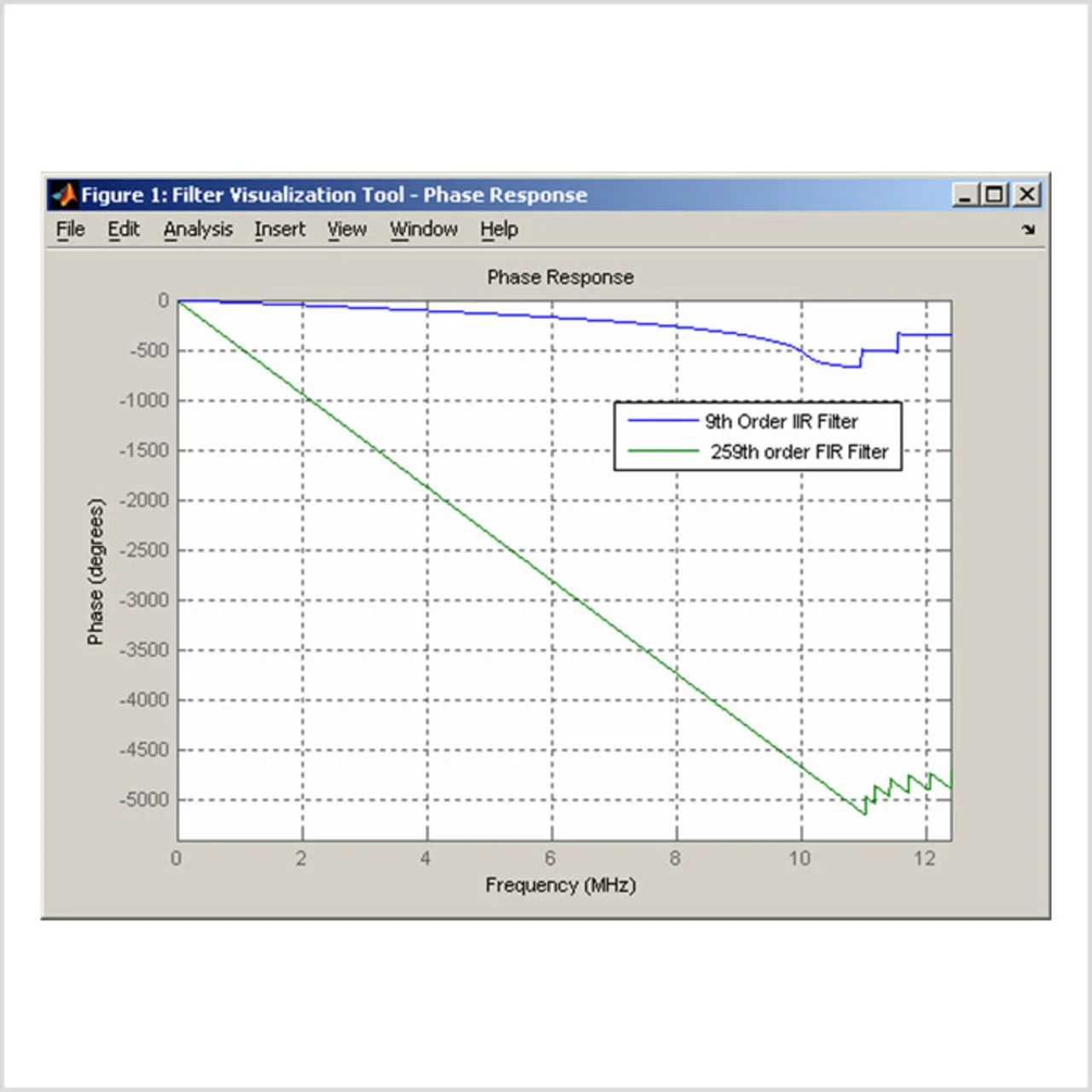
Betrachtet man das Diagramm der Phasenantworten (Bild 2), ist die Phase für das FIR-Filter linear, die Phase des IIRFilters hingegen nicht. Es gibt IIR-Filter, die einen besseren Phasengang liefern, diese werden in diesem Artikel jedoch nicht behandelt.
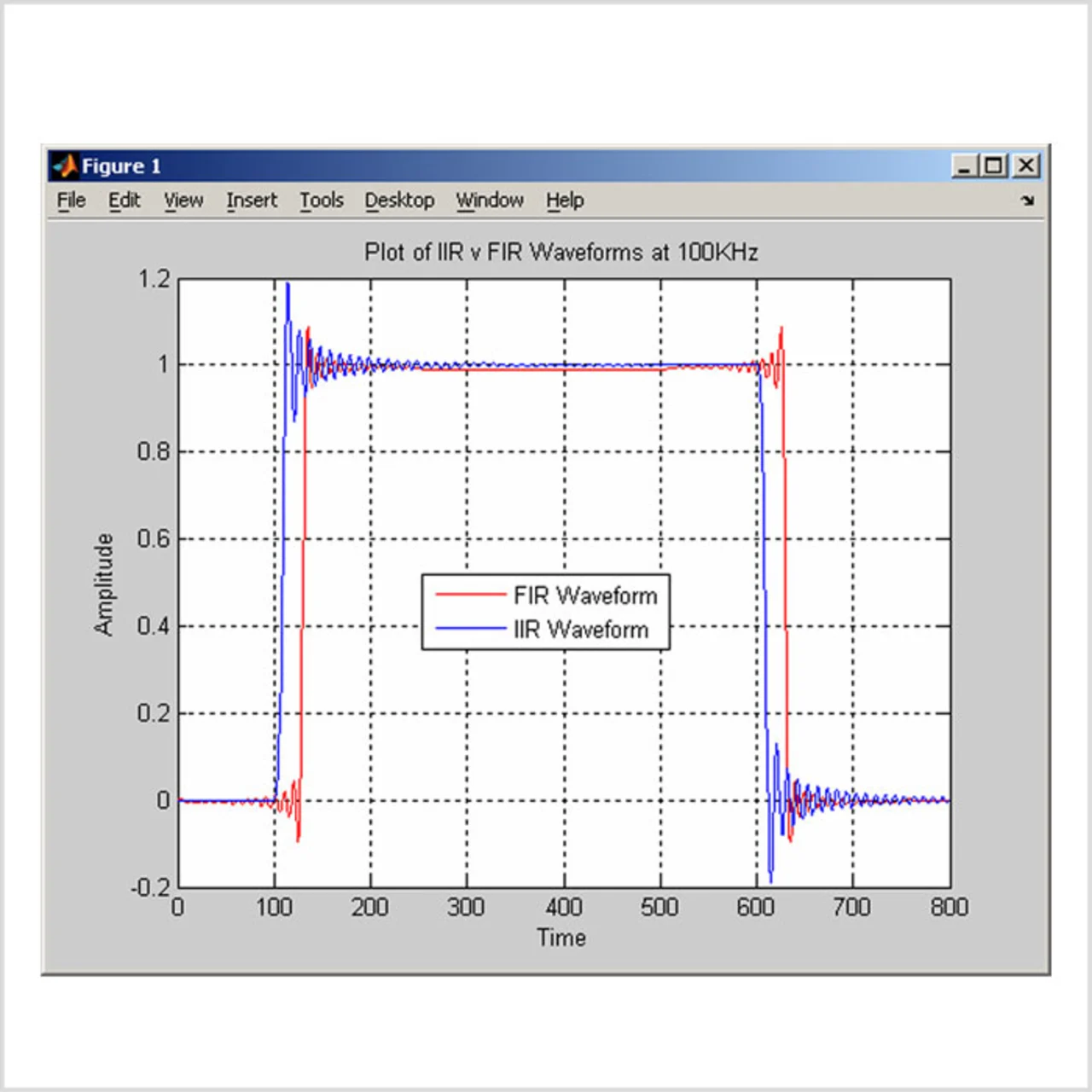
Ein Rechtecksignal beinhaltet beispielsweise unerwünschte Harmonische der Grundfrequenz (Bild 3), weil unterschiedliche Frequenzanteile unterschiedliche Verzögerungen durch ein IIR-Filter haben. Die Latenz durch das IIR-Filter ist jedoch gering.
Klassische IIR-Filter
Abhängig von der Filtercharakteristik kann eine Reihe von IIR-Filterformaten verwendet werden. Die Darstellungen in Bild 4 zeigen den Amplituden- und den Phasengang für die unterschiedlichen IIR-Filter, ausgenommen des Bessel-Filters.
Auch als Cauer-Filter bezeichnet, haben elliptische Filter eine konstante Welligkeit sowohl im Durchlass- als auch im Sperrbereich. Sie erfüllen generell die Anforderungen mit Filtern der kleinsten Ordnung, betrachtet man alle unterstützten Filtertypen.
Für eine vorgegebene Filterordnung, Welligkeit im Durchlass- und Sperrbereich, minimieren elliptische Filter die Durchgangsbandbreite.
Das Butterworth-Filter bietet die beste Annäherung an ein ideales Tiefpassfilter. Durchlass- und Sperrbereich sind besonders flach.
Das Tschebyscheff-Typ-I-Filter minimiert durch Einspeisen der gleichen Welligkeit in den Durchlassbereich die absolute Differenz zwischen der idealen und der aktuellen Frequenzantwort über den gesamten Durchlassbereich. Der Übergang vom Durchlass- zum Sperrbereich erfolgt abrupter als beim Butterworth-Filter.
Abhängig von der Filtercharakteristik kann eine Reihe von IIR-Filterformaten verwendet werden. Die Darstellungen in Bild 4 zeigen den Amplituden- und den Phasengang für die unterschiedlichen IIR-Filter, ausgenommen des Bessel-Filters.
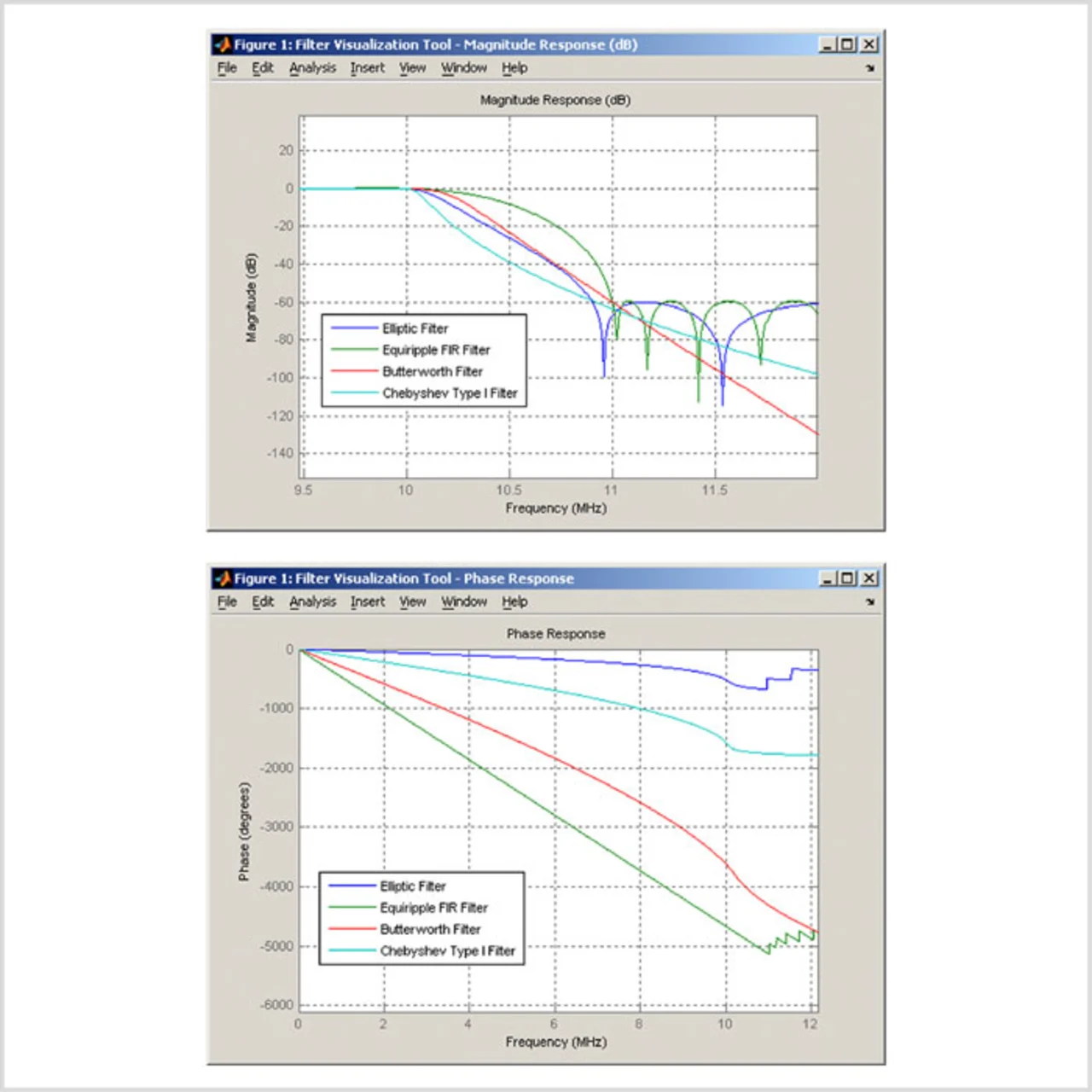
Auch als Cauer-Filter bezeichnet, haben elliptische Filter eine konstante Welligkeit sowohl im Durchlass- als auch im Sperrbereich. Sie erfüllen generell die Anforderungen mit Filtern der kleinsten Ordnung, betrachtet man alle unterstützten Filtertypen. Für eine vorgegebene Filterordnung, Welligkeit im Durchlass- und Sperrbereich, minimieren elliptische Filter die Durchgangsbandbreite.
Das Butterworth-Filter bietet die beste Annäherung an ein ideales Tiefpassfilter. Durchlass- und Sperrbereich sind besonders flach.
Das Tschebyscheff-Typ-I-Filter minimiert durch Einspeisen der gleichen Welligkeit in den Durchlassbereich die absolute Differenz zwischen der idealen und der aktuellen Frequenzantwort über den gesamten Durchlassbereich. Der Übergang vom Durchlass- zum Sperrbereich erfolgt abrupter als beim Butterworth-Filter.
Das Tschebyscheff-Type-II-Filter minimiert ebenfalls die absolute Differenz zwischen der idealen und der aktuellen Frequenzantwort über den gesamten Sperrbereich durch das Einfügen einer gleich großen Welligkeit in den Sperrbereich. Der Frequenzgang im Durchlassbereich ist maximal flach. Der Sperrbereich erreicht den Nullwert nicht so schnell wie das Typ-I-Filter (und erreicht Null überhaupt nicht für gerade Zahlen bei Filtern nter Ordnung). Das Fehlen von Welligkeit im Durchlassbereich ist jedoch häufig ein wichtiger Vorteil.
Analoge Bessel-Tiefpassfilter haben eine maximal flache Gruppenverzögerung bei Null-Frequenz und behalten eine nahezu konstante Gruppenverzögerung über den gesamten Durchlassbereich bei. Gefilterte Signale behalten deshalb ihre Signalformen im Frequenzbereich des Durchlassbereichs bei. Frequenz-gemappte und digitale Bessel-Filter besitzen die Eigenschaft der maximalen Flachheit jedoch nicht. Sie erfordern allgemein ein Filter höherer Ordnung für eine zufriedenstellende Dämpfung des Sperrbereichs als andere Filterarten. Da das MathWorks-Tool das digitale Modell des Bessel-Filters nicht unterstützt, wird dieses Format in diesem Artikel auch nicht beschrieben.
- IIR-Filter in FPGAs implementieren - Teil 1
- Struktur der IIR-Filter