Startseite > E-Mechanik+Passive > Passive > Eng umschlungene, gekoppelte Induktivitäten

Würth Elektronik eiSos

Eng umschlungene, gekoppelte Induktivitäten

19. Februar 2019, 11:00 Uhr | Ralf Higgelke

▶ Diesen Artikel anhören

Fortsetzung des Artikels von Teil 1

Einfluss der Streuinduktivität

Ein Problem bei der Anwendung der gekoppelten Induktivitäten in Schaltnetzteilen ist der Umgang mit der Energie im Streufeld, die durch die Streuinduktivitäten LL_x verursacht wird. Die Folge davon ist eine Resonanz, verursacht durch die parasitären Kapazitäten und der Streuinduktivität. Durch die Resonanz können hohe Spannungsspitzen am Mosfet entstehen, die es zu begrenzen gilt.

Betrachtet man die beiden Wicklungen der gekoppelten Induktivität, so ist die Gesamtmenge des von einer Wicklung erzeugten Flusses nicht vollständig mit der zweiten Wicklung gekoppelt. Jeder magnetische Flussanteil der Primärwicklung, der nicht in die Sekundärwicklung einkoppelt, wirkt als induktive Impedanz in Reihe mit der Primärwicklung. Daher wird diese Streuinduktivität im Ersatzschaltbild in Bild 4 durch zusätzliche Induktivitäten LL₁ und LL₂ dargestellt. Um den Streueffekt zu verdeutlichen, ist in Bild 5 das Schaltbild einer gekoppelten Induktivität ohne Verluste, jedoch mit Streuinduktivitäten dargestellt.

Jobangebote+ passend zum Thema

Ingenieur/Elektroingenieur/Elektrotechniker als Field Application Engineer

GEYER Electronic GmbH, Planegg

Alle Jobangebote im Elektroniknet Karrierebereich anzeigen

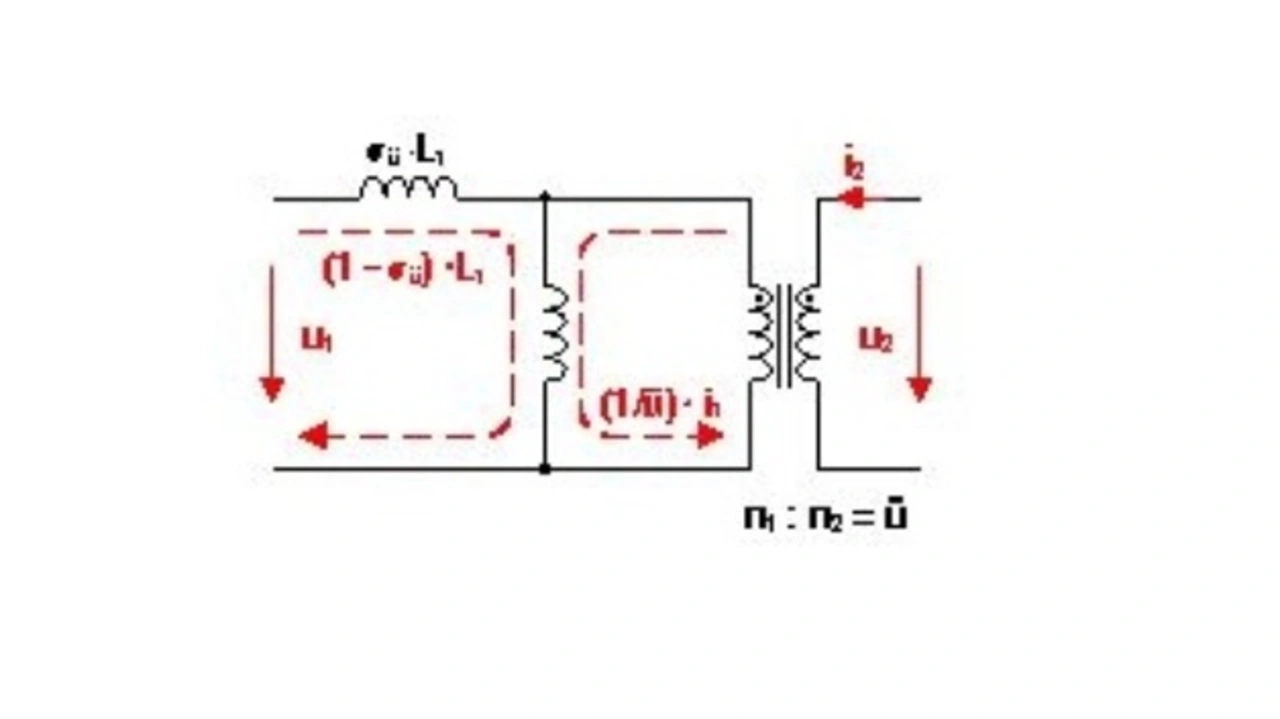
Der Streufaktor σ_ü ist ein Maß für den Teil des Feldes, der nicht durch beide Wicklungen des Transformators fließt und lässt sich wie folgt beschreiben:

(8) $sigma subscript ü equals 1 minus fraction numerator M squared over denominator L subscript 1 times L subscript 2 end fraction$

Dabei kann dieser Streufaktor einen Wert zwischen 0 und 1 annehmen; σ_ü = 0 bedeutet, dass keine Streuinduktivität vorliegt, σ_ü = 1, dass keine Kopplung zwischen den beiden Wicklungen des Transformators besteht. Die Induktivität σ_ü ∙ L₁ in Bild 5 wird als Streuinduktivität bezeichnet; (1 – σ_ü) ∙ L1 ist die Induktivität, die zur gewünschten Funktion beiträgt. Das Übersetzungsverhältnis ü der Wicklungen beträgt:

(9) $ü equals square root of L subscript 1 over L subscript 2 times open parentheses 1 minus sigma subscript ü close parentheses end root$

Daraus lässt sich die Gegenkopplungsinduktivität M ableiten:

(10) $M equals open parentheses 1 minus sigma subscript ü close parentheses times L subscript 1 times fraction numerator 1 over denominator u with ¨ on top end fraction$

Damit ergibt sich für die Sekundärinduktivität L₂:

(11) $L subscript 2 equals open parentheses 1 minus sigma subscript ü close parentheses times L subscript 1 times 1 over ü squared$

Um zu verstehen, wie sich die Streuinduktivität in der Praxis minimieren lässt, müssen die sie beeinflussenden Parameter bekannt sein. Die Induktivität einer zylindrischen Spule (Bild 6a) definiert sich wie folgt:

(12) $L subscript 1 equals fraction numerator mu subscript 0 times N squared times A subscript 1 over denominator l subscript w end fraction$

Kommt nun eine zweite Wicklung über die erste (Bild 6b), hat die zweite Wicklung die Induktivität L₂:

(13) $L subscript 2 equals fraction numerator µ subscript 0 times N squared times A subscript 2 over denominator l subscript w end fraction$

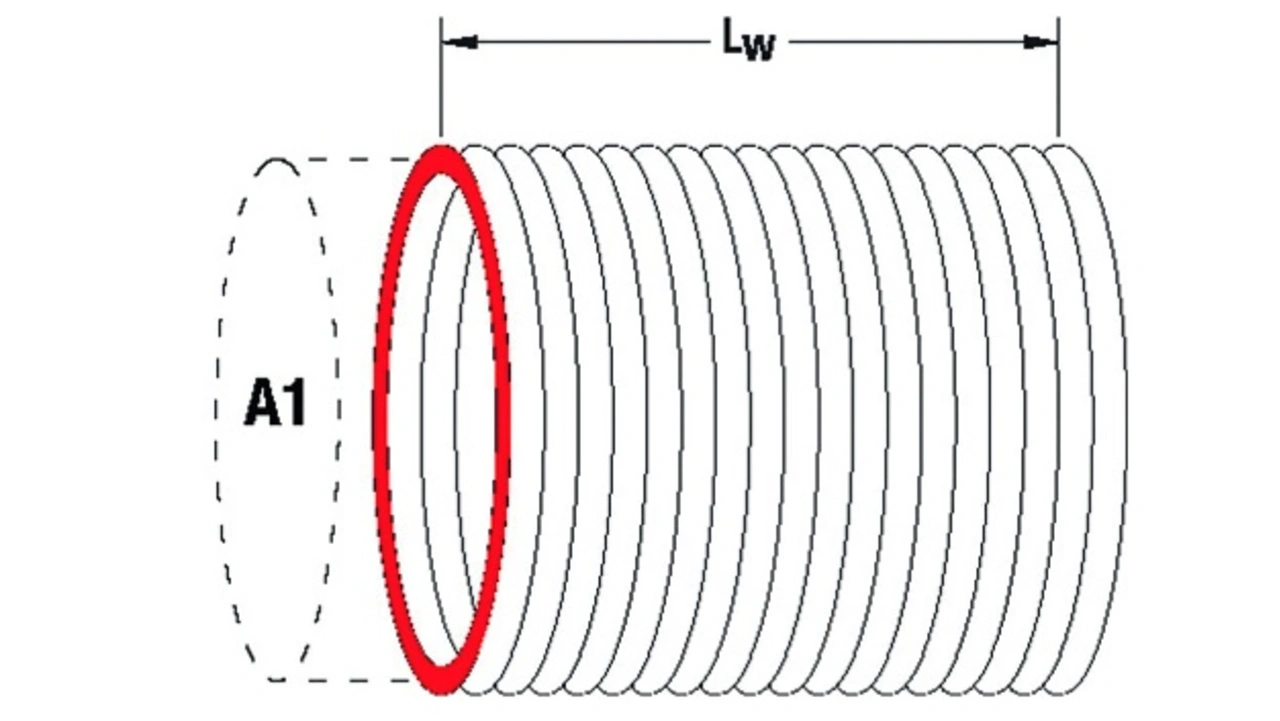
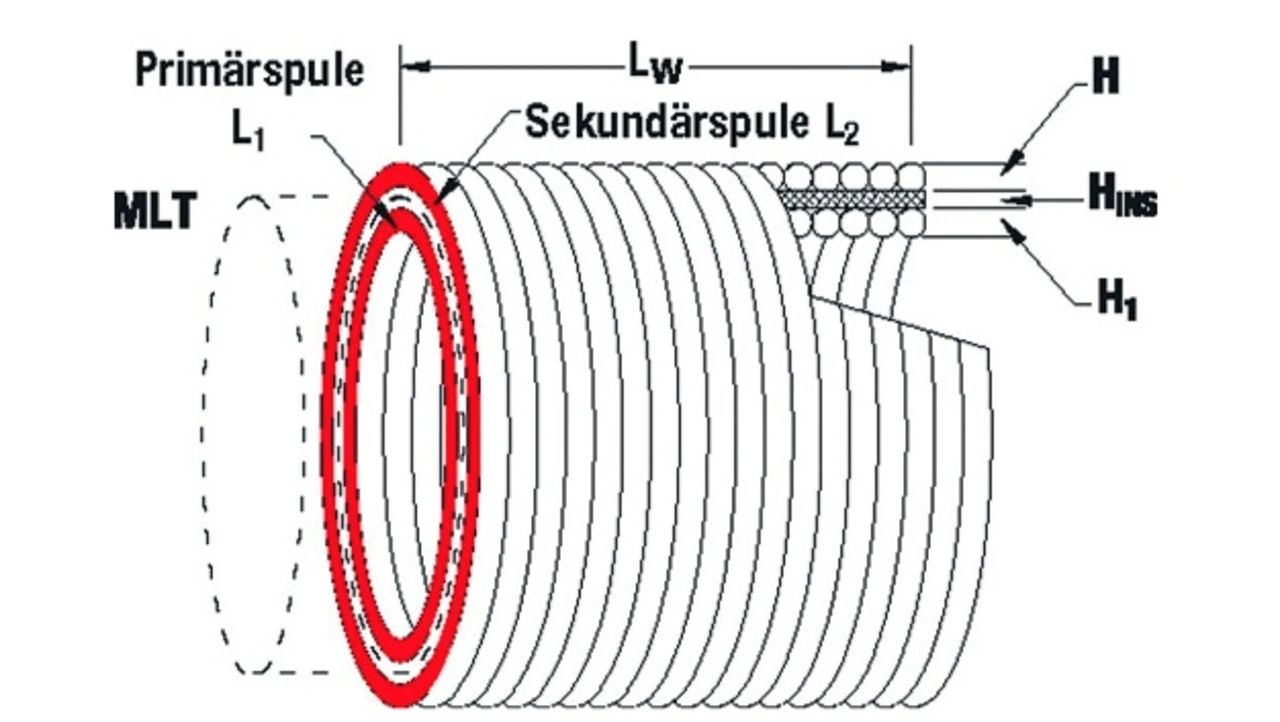
A₁ und A₂ sind die Flächen jeder einzelnen Wicklung, ∆A ist die Flächendifferenz zwischen den beiden Wicklungen. Der Unterschied der Induktivität ∆L zwischen den beiden Wicklungen beträgt somit:

(14) $capital delta L equals fraction numerator µ subscript 0 times N squared times capital delta A over denominator l subscript w end fraction$

Die Differenz der einzelnen Spulenflächen lässt sich berechnen mit:

(15) $capital delta A equals M L T times open parentheses H subscript i n s end subscript plus H subscript 1 over 3 plus H subscript 2 over 3 close parentheses$

Dabei ist MLT die durchschnittliche Wicklungslänge, H_ins der Abstand zwischen den Wicklungen (Isolierung), H₁ und H₂ sind die Dicken der beiden Wicklungen.

Die Streuinduktivität ist somit unabhängig vom Kernmaterial und von einem Luftspalt in einem Kern. Hauptfaktoren für die Streuinduktivität sind die geometrischen Unterschiede der beiden Wicklungen. Um die Streuinduktivität der Spule in Bild 6b zu minimieren, ist entweder die Länge der Spule L₁ zu vergrößern oder der Abstand zwischen den Wicklungen zu verringern.

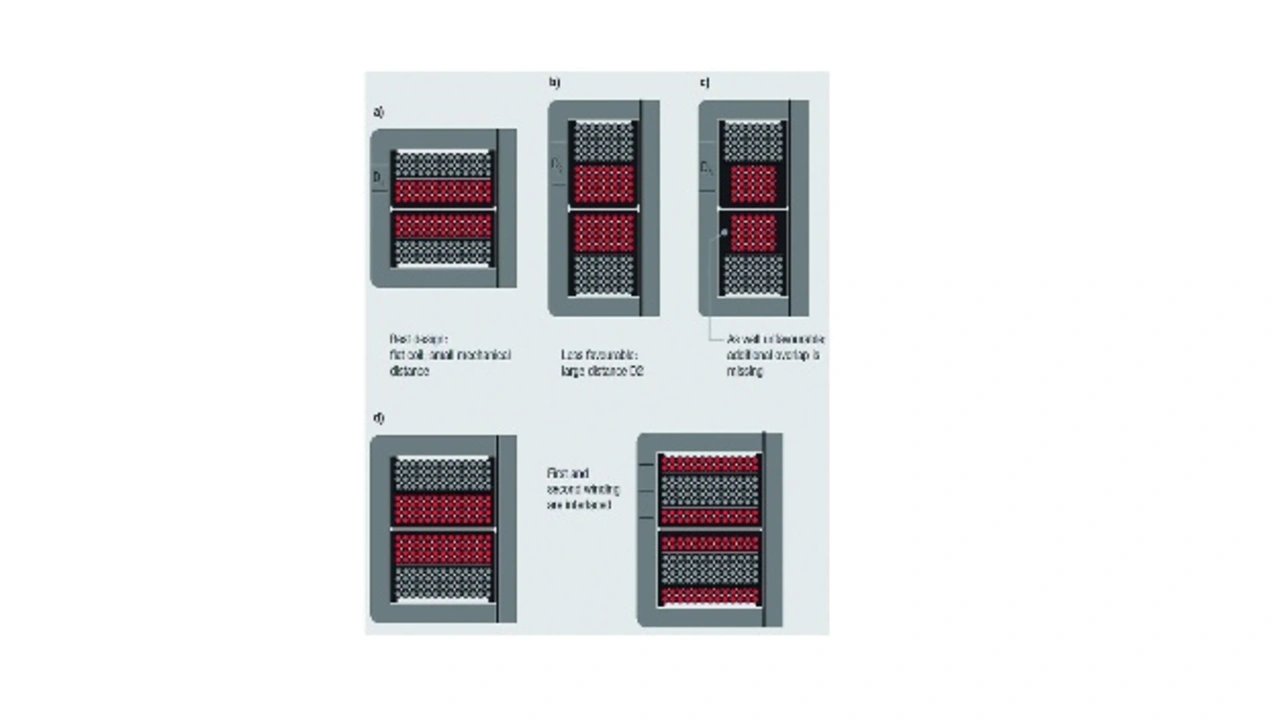
Daher muss die Fläche A₁ der Fläche A₂ entsprechen. Das lässt sich erreichen, indem man beispielsweise beide Spulen bifilar auf den gleichen Kern wickelt. Bild 7 zeigt verschiedene mögliche Wicklungskonfigurationen. Bei der vorhandenen Geometrie ist das am häufigsten verwendete Mittel eine Sandwich-Konstruktion (Bild 7, unten rechts), bei der die Sekundärwicklung zwischen der geteilten Primärwicklung gewickelt ist.