Fortschritt: selten geradlinig
Neue Wandlerarchitekturen und -techniken
Fortsetzung des Artikels von Teil 3
»Compressive Sampling«-A/D-Wandler
Legitimation für Compressive-Sampling-A/D-Wandler
Anwendungen wie beispielsweise Kommunikationssysteme oder Hochleistungsmessgeräte verarbeiten sehr aktive Signale. In Sensoranwendungen der Bereiche Gesundheits-/Vitalüberwachung, Erdbeben-/Umweltüberwachung und Prozesssteuerungen hingegen müssen Signale verarbeitet werden, die sich mit Ausnahme von kurzen Aktivitäten über längere Zeiträume nur sehr wenig verändern.
Andere Signalklassen (beispielsweise im Audiobereich) lassen sich entweder durch wenige signifikante Frequenzkomponenten oder durch begrenzte Aktivitäten im Zeitbereich darstellen. Deshalb werden solche Signale als »spärlich« bezeichnet: spärlich im Frequenzbereich und spärlich im Zeitbereich.
Das Abtasttheorem von Shannon, bei dem eine zeitkontinuierliche Abtastung mit einer Rate erfolgt, die mindestens das Doppelte der höchsten Frequenzkomponente beträgt, ist zwar gültig, aber bei spärlichen Signalen nicht sehr effizient. Denn dies würde zu einer sehr langen Abtastreihe führen, die zwar das Signal erfasst, aber zu viele Abtastungen/Daten benötigt, um den gewünschten Informationsgehalt zu liefern.
Das Thema »Signal Sparsity« und die damit verbundene Verarbeitung ist zwar seit mehreren Jahrzehnten in vielen technischen Disziplinen bekannt (beispielsweise sind Kompressionsalgorithmen im Softwaredesign und in der Datenspeicherung allgegenwärtig und die Wavelet-Theorie in der Signalverarbeitung gut etabliert), hat aber in letzter Zeit aufgrund des Wachstums im IoT-Bereich bei Schaltungsentwicklern neue Aufmerksamkeit gefunden.
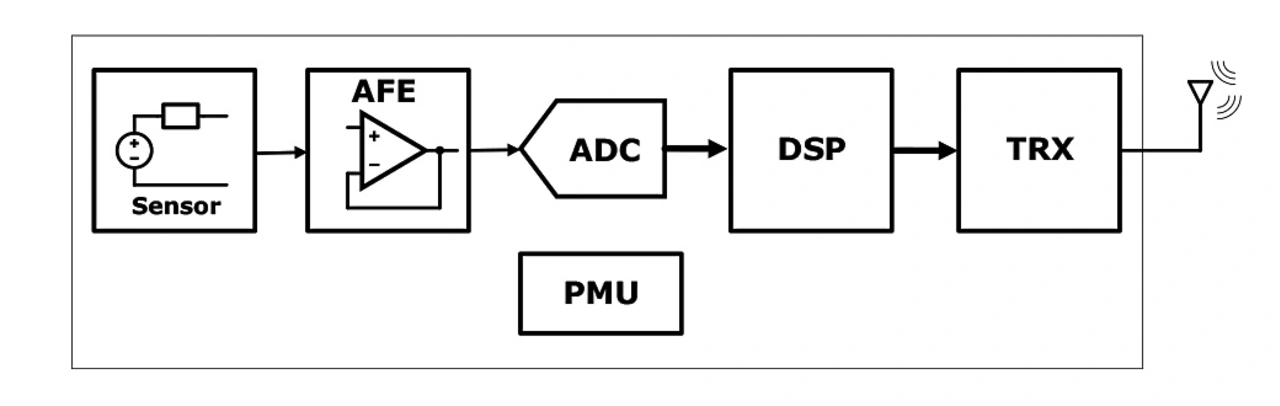
Dies gilt insbesondere für drahtlose Sensornetzwerke (WSNs). Dazu erfasst ein Netz von Sensorknoten (SN) bestimmte sensorische Informationen, verarbeitet sie vor und übermittelt sie drahtlos an einen zentralen Hub/Basisstation. Jeder SN besteht aus Sensoren, der Signalaufbereitungs- und Datenerfassungsschaltung, einem lokalen DSP und dem drahtlosen Transceiver (TRX) plus einer Stromversorgung (Bild 6).
Die mit den SNs verbundenen Anforderungen an Größe, Gewicht und Leistung (SWAP) sind äußerst hoch. Während jeder Schaltungsblock in der Signalkette, aus der das SN besteht, die entsprechenden Spezifikationen erfüllen muss, liegen die wirklichen Engpässe sowie und die leistungshungrigsten Funktionen in mehreren Fällen entweder in der Datenübertragung vom SN zum Hub (TRX) oder in der digitalen Signalverarbeitung (DSP) des SN. Die Signalverarbeitung ist erforderlich, um die relevanten Informationen aus den an den Hub zu sendenden Daten zu extrahieren.
Relativ gesehen verbraucht der A/D-Wandler nur einen sehr bescheidenen Teil des gesamten Energiebudgets (beispielsweise ~5% der gesamten Leistungsaufnahme des SNs). Ist der A/D-Wandler jedoch ein klassischer Shannon-Wandler (zeitkontinuierliche Abtastrate), so erzeugt er eine sehr große Datenmenge. Diese führt dazu, dass der DSP und/oder der TRX mehr Leistung benötigen.
Jobangebote+ passend zum Thema
In solchen Fällen besteht die Herausforderung bei einem Wandler darin, eine Architektur mit komprimierter Abtastung (CS) zu entwickeln, die bei der Analog/Digital-Wandlung weniger Daten erzeugt und somit die Leistungsaufnahme des SN senkt. Die komprimierten Informationen werden dann an den Hub übertragen, wo mit wesentlich mehr Rechenkapazität und größerem Leistungsbudget die Rekonstruktion des empfangenen komprimierten Signals in das ursprüngliche erfasste Signal durchgeführt werden kann.
Compressive-Sampling-Architekturen
Die Fachliteratur beschreibt verschiedene Implementierungsansätze für Compressive Sampling. Nach dem Shannon-Abtasttheorem kann ein im Zeitbereich abgetastetes Signal als eine Modulation/Faltung zwischen dem ursprünglichen kontinuierlichen Eingangssignal und einer Dirac-Impulsfolge betrachtet werden.
Beim Compressive Sampling wird die Impulsfolge durch impulsamplitudenmodulierte Signale ersetzt, deren Amplitude durch unabhängige, gleichmäßig verteilte Rauschvektoren (idealerweise Gaußsche Vektoren) definiert ist (normalerweise eine pseudozufällige binäre Sequenz oder PRBS). Diese bilden eine alternative Darstellungsgrundlage. Bei einem spärlichen Eingangssignal hat das resultierende Signal nach der Faltung mit den PRBS-Signalen (der Kompression) weitaus weniger Abtastwerte. Um das ursprüngliche Signal anschließend wiederherstellen zu können, muss der Vorgang mit tolerierbaren/kontrollierbaren Verlusten/Verschlechterungen reversibel sein.
Im Allgemeinen kann man sich den Komprimierungsvorgang als eine Matrixmultiplikation zwischen dem Vektor der Abtastwerte des ursprünglichen Eingangssignals und einer Verschlüsselungsmatrix aus geeigneten PRBS-Vektoren vorstellen (die Faltung besteht aus einem inneren Produkt der Eingangssignalsequenz mit den Basisvektoren). Die Komprimierung kann in verschiedenen Stufen der Signalkette erfolgen (Bild 6). Dies kann im analogen zeitkontinuierlichen Bereich vor dem A/D-Wandler geschehen.
In diesem Fall kann die Abtastrate des A/D-Wandlers auf eine Sub-Nyquist-Rate verringert werden. Die Verschlüsselung übernimmt eine analoge Faltungsschaltung. Sie könnte jedoch auch im digitalen Bereich, nach dem A/D-Wandler, erfolgen und vom DSP durchgeführt werden.
In diesem Fall ist der A/D-Wandler ein herkömmlicher Wandler mit gleichmäßiger Abtastung (nach Nyquist), und die Verschlüsselung übernimmt der DSP. Alternativ kann sie im analogen Bereich durchgeführt werden, kombiniert mit der Wandlerfunktion (die mit Sub-Nyquist-Rate läuft), was zu Compressive-Sampling-A/D-Wandler-Architekturen führt.
Die hier beschriebenen Systeme sind Beispiele für den Fall, dass die Kompression im analogen Bereich vor dem A/D-Wandler erfolgt. Zur Implementierung des Encoders dient eine RMPI-Architektur (Random Modulation Pre-Integrator) mit mehreren parallelen Signalpfaden. Jeder Signalpfad enthält einen Mischer mit einer anderen Zufallsbasisfunktion. Nachgeschaltet sind eine Tiefpass/Integratorstufe und ein A/D-Wandler mit verringerter Abtastrate (in der Regel ein SAR-Wandler).
Während die Mischer mit ±1 Zufallskomponenten effizient analog implementiert werden können, erfordert die Filterung/Integration Transkonduktanzverstärker (OTAs) mit hohem Platz- und Energiebedarf. Die A/D-Wandler arbeiten mit einer niedrigen Abtastrate und nehmen bei geringem Platzbedarf wenig Leistung auf. Hingegen kann der Rest des Analog-Encoders sehr viel Leistung und viel Platz benötigen. Außerdem erfordern die parallelen Pfade eine geeignete zeitliche Ausrichtung, was zusätzliche Herausforderungen für die Entwicklung mit sich bringt.
In entsprechender Literatur hingegen wird der CS-Encoder digital implementiert. Hier werden die Integratoren durch energieeffiziente digitale Akkumulatoren ersetzt, obwohl der sehr energieeffizient implementierte A/D-Wandler mit Nyquist-Frequenz läuft.
Eine ganz andere Art, CS zu realisieren, wird in anderer Literatur vorgestellt. Hier wird das Mischen des Eingangssignals mit den PBRS-Basisfunktionen und die anschließende Integration durch eine wesentlich einfachere Architektur ersetzt, bei welcher der Sampler vor dem A/D-Wandler tatsächlich von der PBRS gesteuert wird. Anders ausgedrückt: Anstatt N aufeinanderfolgende Werte mit einer einheitlichen Rate fs abzutasten, wählt der CS-Sampler nur M von ihnen nach dem Zufallsprinzip (mit M<N) aus jedem aufeinanderfolgenden Fenster der Länge N des Eingangssignals aus.
Die daraus resultierende Zeitfolge beim ungleichförmigen Abtasten (Non-Uniform Sampling, NUS) entspricht dann einer niedrigeren Abtastrate von durchschnittlich M⁄N fs und wird von einem A/D-Wandler digitalisiert. Dieser ist strukturell identisch mit einem herkömmlichen asynchronen SAR-A/D-Wandler. Allerdings wird jeder Wandlungszyklus durch den PBRS-Takt des Samplers flankengetriggert.
Eine weitere Implementierung, die mit einem ähnlichen Prinzip des Non-uniform Sampling arbeitet, ist in einer anderen Fachliteratur beschrieben. Die Implementierungen, die das NUS Compressive Sampling Framework verwenden, haben den Vorteil, dass sie eine eher vereinfachte Hardware-Implementierung im SN bieten (dadurch wird ein größerer Teil des Dekompressionsvorgangs auf den Hub/die Basisstation verlagert). Allerdings zeigen sie gegenüber den Alternativen auch eine geringere Leistungsfähigkeit in Bezug auf die Spärlichkeit der Signale, die sie verarbeiten können.
Ein sehr effektiver Ansatz wird schließlich in einem weiteren Fachbericht vorgestellt. In diesem Fall wird ein SAR-A/D-Wandler durch ein erweitertes Frontend ergänzt, welches die CS-Verschlüsselung zeitdiskret durchführt. Das Mischen mit den PBRS-Sequenzen erfolgt ähnlich wie bei den RMPI-Implementierungen mit passiven Vierfach-Mischern, wobei die zeitdiskrete Implementierung Vorteile gegenüber den in den RMPI-Architekturen verwendeten zeitkontinuierlichen Schaltungen hat.
Ferner wird die anschließende Integrationsoperation im Ladungsbereich mit einer rekonfigurierbaren Erweiterung des kapazitiven D/A-Wandler-Arrays des SAR-A/D-Wandlers selbst durchgeführt. Dadurch lässt sich der Einsatz von leistungshungrigen OTAs mit großem Platzbedarf, wie sie in früheren RMPI-Architekturen verwendet wurden, vermeiden, und es kommen lediglich passive Switched-Capacitor-Schaltungen zum Einsatz.
Die hier erläuterten Beispiele zeigen sehr ermutigende Fortschritte, die in einem begrenzten Zeitraum erzielt wurden. Der Fokus auf die Leistungseffizienz des Wandlers selbst ist nicht so wichtig.
Der Hauptgrund für die Entwicklung eines A/D-Wandlers mit komprimierter Abtastung (Compressive Sampling) liegt in den erheblichen Auswirkungen auf die Signalkette und die Gesamtleistung des SN, nicht aber auf den A/D-Wandlern.
Der Autor:

Gabriele Manganaro hat einen Dr.-Ing. und einen Ph.D. in Elektronik von der Universität Catania, Italien. Ab 1994 forschte er bei STMicroelectronics und an der Texas A&M University. Er arbeitete im Bereich IC-Design für Datenkonverter bei Texas Instruments, Engim Inc. und als Design Director bei National Semiconductor. Seit 2010 ist er bei Analog Devices tätig, zunächst als Engineering Director für Hochgeschwindigkeitsdatenwandler und seit kurzem als Technology Director in der Wireless Communication Products Division. Er war sieben Jahre in Folge Mitglied des technischen Unterausschusses für Datenwandler der ISSCC. Er war Mitherausgeber der Zeitschrift IEEE Trans. On Circuits and Systems - Part II und dann Associate Editor, stellvertretender Chefredakteur und schließlich Chefredakteur für IEEE Trans. On Circuits and Systems - Part I. Derzeit ist er der Chefredakteur des IEEE Open Journal of Circuits and Systems. Er ist Autor bzw. Mitautor von mehr als 60 von Fachleuten begutachteten Artikeln, drei Büchern (insbesondere Advanced Data Converters", Cambridge University Press, 2011) und hat 17 US-Patente erhalten, weitere sind anhängig. Er erhielt wissenschaftliche Auszeichnungen, darunter 1995 den CEU Award des Rutherford Appleton Laboratory (UK), 1999 den IEEE Circuits and Systems Outstanding Young Author Award und 2007 den IEEE European Solid-State Circuits Conference Best Paper Award. Er ist ein IEEE Fellow (seit 2016), ein Fellow of the IET (seit 2009), Mitglied der wissenschaftlichen Ehrengesellschaft Sigma Xi und war Mitglied des Board of Governors der IEEE Circuits and Systems Society (2016-18). Er ist Distinguished Lecturer für die IEEE Solid-State Circuits Society (Amtszeit 2019-20) und beratendes Mitglied für die Proceedings of the IEEE.
DC/DC-Wandler im Mikromodul-Format
Klein, aber definitiv »oho«
Ansteuerung von SiC-MOSFETs
Vorteile digitaler Gate-Treiber
Frederik Dostal/Analog Devices
Strom/Spannung muss immer verfügbar sein
GreenPak
Immer konfigurierbar, jetzt noch erfolgreicher
Schaltregler
EMV-Störungen von Speicherdrosseln minimieren
Stromversorgungen
Wie lassen sich typische Fehler im PCB-Layout…
Operationsverstärker
OPVs für batteriebetriebene IIoT-Anwendungen
Texas Instruments
Höhere Leistungsdichte dank integrierter…
Viel Know-how notwendig
Isolierte Controller
Galliumnitrid
Integrierte GaN-Gate-Treiber im Vergleich
Vorstellung einer Messmethode
Sind die ADCs für wirklich raue Einsatzbedingungen…
Fortschritt: selten geradlinig
Neue Wandlerarchitekturen und -techniken
Das Maximum herausholen
Hochauflösende schnelle ADCs brauchen ADC-Treiber
Advertorial
Kompakt, robust und selbstschirmend
- Neue Wandlerarchitekturen und -techniken
- Technologischer Durchbruch bei Wandlern als Enabler
- TDC und DTC (Zeit/Digital- und Digital/Zeit-Wandler)
- »Compressive Sampling«-A/D-Wandler