Startseite > Embedded > Hardware > TCP/IP über Raspberry Pi

Fünf-Achsen-Roboterarm

TCP/IP über Raspberry Pi

5. Dezember 2017, 9:00 Uhr | Chris Henschel, Gründer Henschel-Robotics

▶ Diesen Artikel anhören

Fortsetzung des Artikels von Teil 3

Kinematik

Es gibt verschiedene Lösungsansätze der Vorwärts- und Rückwärtskinematik an einem Knickarmroboter. In diesem Fall konnten die Gleichungen symbolisch gelöst werden, was auf die mechanische Konstruktion des Roboters zurückzuführen ist. Bei der Vorwärtskinematik, welche meist einfacher zu rechnen ist, wurde das Prinzip von Denavit-Hartenberg angewandt.

Jobangebote+ passend zum Thema

MACNICA ATD EUROPE - Ihre berufliche Zukunft

MACNICA ATD Europe GmbH, Ingolstadt

Alle Jobangebote im Elektroniknet Karrierebereich anzeigen

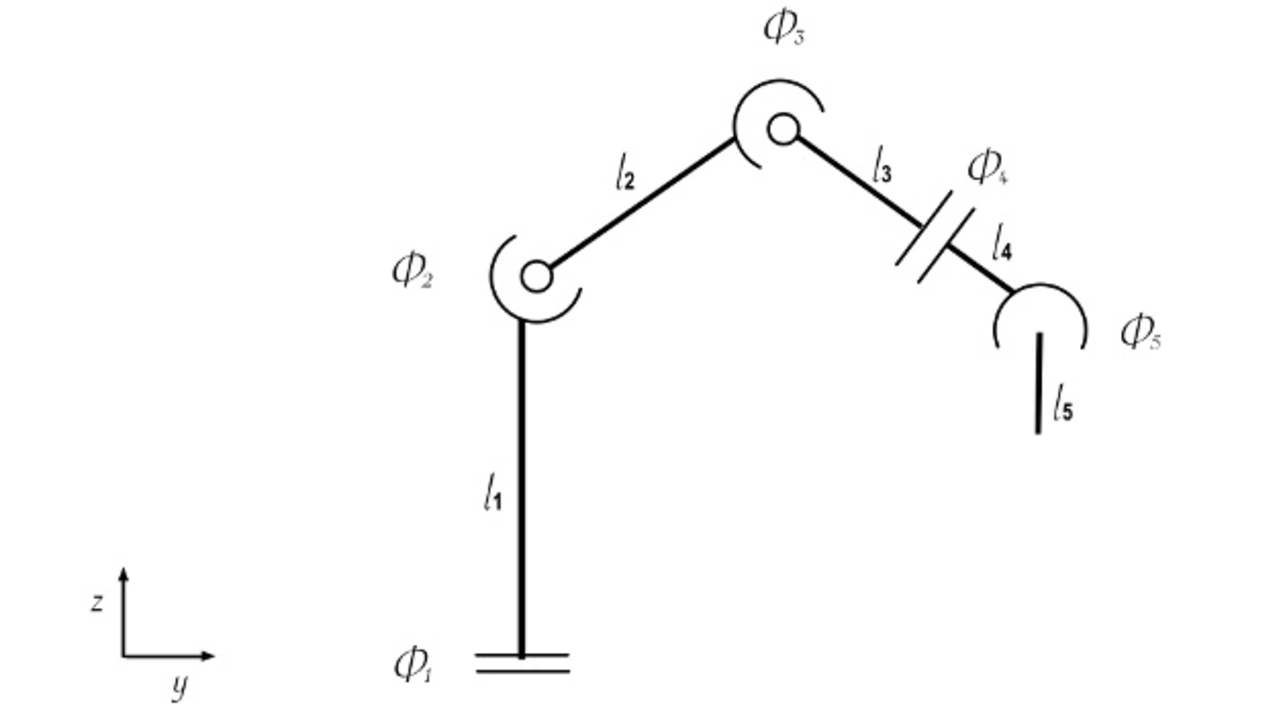
Hierzu wird im Ursprung (der Robotersockel) begonnen und schrittweise bis zum Ziel gerechnet. Bei den Transformationsmatrizen wurden homogene 4x4 Matrizen verwendet, welche zugleich die Translation sowie auch die Rotation um jede Achse im Raum abbilden. Um nun vom Sockel bis zur Spitze des Endeffektors (Tool Center Point) zu gelangen, werden jeweils die Ursprungskoordinaten mit der Transformationsmatrix auf die nächste Achse multipliziert. Dieser Prozess wird iteriert womit die Transformationsmatrix vom Ursprung auf den TCP entsteht.

Die Rotations- und Translations-Matrizen sind dabei:

$T subscript r o t X end subscript equals open parentheses table row 1 0 0 0 row 0 c cell negative s end cell 0 row 0 s c 0 row 0 0 0 1 end table close parentheses comma space T subscript r o t Y end subscript equals open parentheses table row c 0 s 0 row 0 1 0 0 row cell negative s end cell 0 c 0 row 0 0 0 1 end table close parentheses comma space T subscript r o t Z end subscript equals open parentheses table row c cell negative s end cell 0 0 row s c 0 0 row 0 0 1 0 row 0 0 0 1 end table close parentheses T subscript T r a n s end subscript equals open parentheses table row 1 0 0 x row 0 1 0 y row 0 0 1 z row 0 0 0 1 end table close parentheses$

(s und c entsprechen sin( $theta$ ) bzw. cos( $theta$ ))

Die Berechnung startet nun am Sockel im Koordinatenursprung.

$T subscript S t a r t end subscript equals open parentheses table row 1 0 0 0 row 0 1 0 0 row 0 0 1 0 row 0 0 0 1 end table close parentheses$

In 1 wird nun vom Sockel zur Achse 2 gerechnet: Erst wird um die Z-Koordinate, welche die vertikale Roboterlage beschreibt, gedreht, danach um die erste Länge $l subscript 1$ , die Turm-Höhe, verschoben. Dann wird von Achse 2 zu 3 gerechnet und iteriert. Die Parameter $theta subscript 1 minus 5 end subscript$ beschreiben die fünf Achsenwinkel des Roboters, $l subscript 1 minus 5 end subscript$ sind die jeweiligen Achsenabstände.

$1 right parenthesis space T subscript 0 minus 1 end subscript equals T subscript S t a r t end subscript ring operator T subscript r o t Z end subscript left parenthesis theta subscript 1 right parenthesis ring operator T subscript t r a n s end subscript left parenthesis 0 comma 0 comma l subscript 1 right parenthesis 2 right parenthesis space T subscript 0 minus 2 end subscript equals T subscript 0 minus 1 end subscript ring operator T subscript r o t Y end subscript left parenthesis theta subscript 2 right parenthesis ring operator T subscript t r a n s end subscript left parenthesis 0 comma 0 comma l subscript 2 right parenthesis 3 right parenthesis space T subscript 0 minus 3 end subscript equals T subscript 0 minus 2 end subscript ring operator T subscript r o t Y end subscript left parenthesis theta subscript 3 right parenthesis ring operator T subscript t r a n s end subscript left parenthesis 0 comma 0 comma l subscript 3 plus l subscript 4 right parenthesis 4 right parenthesis space T subscript 0 minus 4 end subscript equals T subscript 0 minus 3 end subscript ring operator T subscript r o t Z end subscript left parenthesis theta subscript 4 right parenthesis 5 right parenthesis space T subscript 0 minus 5 end subscript equals T subscript 0 minus 4 end subscript ring operator T subscript r o t Y end subscript left parenthesis theta subscript 5 right parenthesis ring operator T subscript t r a n s end subscript left parenthesis 0 comma 0 comma l subscript 5 right parenthesis$

Die resultierende 4x4-Matrix $T subscript 0 minus 5 end subscript$ beschreibt sämtliche Translationen und Rotationen vom Ursprung bis zum Endeffektor. Unter Einrechnen der Achsenwinkel und konstanten Achsenabstände des Roboters können die Zielkoordinaten in der letzten Spalte der Matrix als x, y und z einfach abgelesen werden. Somit ist die Transformation von den Gelenkwinkeln auf den Roboter-TCP bekannt. Ebenso enthält die Transformationsmatrix die beiden Endeffektor-Lagewinkel, die mit inverser Kinematik extrahierbar sind.

Diese Rückwärtskinematik gestaltet sich etwas aufwändiger. Dabei wird eine im Raum durch x, y, z und zwei Eulerwinkel angegebene Zielpose auf die einzelnen Robotor-Achsenwinkel zurückgerechnet. Dazu existieren verschiedene numerische wie symbolische Verfahren. Bei der gewählten geometrischen Roboterkonfiguration, in der sich die letzten drei Achsen in einem Punkt schneiden, ist eine symbolische Lösung vorhanden. Hier gibt es für jede Pose 8 Lösungen, wobei die meisten entweder mechanisch oder energetisch keinen Sinn ergeben. Als Beispiel könnte man zu jedem Zielpunkt bei der Achse 1 in beide Richtungen fahren. Steht die Achse 1 auf 0° und die Zielposition der Achse 1 entspräche 20°, so gibt es die zwei Lösungen +20° oder -340°. Die implementierte Kinematik-Berechnung berücksichtigt nicht alle diese Lösungen, welche bei industriellen Knickarm-Robotern als Konfiguration mitgegeben werden könnten.

Bei der Berechnung wird mit den translatorischen Zielkoordinaten begonnen:

$T subscript S t a r t end subscript equals open parentheses table row 1 0 0 x row 0 1 0 y row 0 0 1 z row 0 0 0 1 end table close parentheses$

Nach Multiplikation der Endlage in den TCP

$T subscript 0 minus 5 end subscript equals T subscript S t a r t end subscript ring operator T subscript r o t Z end subscript left parenthesis alpha right parenthesis ring operator T subscript r o t Y end subscript left parenthesis beta right parenthesis$

folgt $T subscript 0 minus 5 end subscript$ , was bereits die Transformation vom Ursprung bis zur letzten Achse bedeutet. In der inversen Kinematik ist das Roboterziel bekannt.

Zur Extraktion der Achsenwinkel wird zunächst von der vorgegebenen TCP-Lage mit Denavit-Hartenberg zurück zum Handgelenk gerechnet:

$T subscript 3 minus 5 end subscript equals T subscript 0 minus 5 end subscript ring operator T subscript t r a n s end subscript left parenthesis 0 comma 0 comma l subscript 4 right parenthesis$

In der letzten Spalte Matrix $T subscript 3 minus 5 end subscript$ stehen jetzt die Koordinaten der Handgelenkposition q₁, q₂, q₃ des Roboters. Es gilt die Roboterlagewinkel $theta subscript 1 minus 3 end subscript$ zu finden, welche diese Position erreichen können.

Dieses Problem ist weniger komplex und geometrisch lösbar.

$theta subscript 1 equals a tan open parentheses 2 asterisk times q subscript 2 asterisk times q subscript 1 close parentheses theta subscript 3 equals pi minus a cos open parentheses fraction numerator a to the power of 2 space end exponent plus b squared minus c squared over denominator 2 asterisk times a asterisk times b end fraction close parentheses$

wobei

$b equals l subscript 2 asterisk times a equals l subscript 3 plus l subscript 4 space end subscript theta subscript 2 equals a cos open parentheses fraction numerator q subscript 3 minus l subscript 1 over denominator q subscript 1 squared plus q subscript 2 squared plus left parenthesis q subscript 3 minus l subscript 1 right parenthesis squared end fraction close parentheses minus a cos open parentheses fraction numerator b squared plus c squared minus a squared over denominator 2 asterisk times b asterisk times c end fraction close parentheses$

Mit den ersten drei bekannten Roboterwinkeln wird vom Sockel wieder bis zum Handgelenk hochgerechnet, sodass $T subscript 0 minus 3 end subscript$ bekannt wird. Die letzten zwei Roboterwinkel liefert folgender Trick: Da $T subscript 0 minus 3 end subscript ring operator T subscript 3 minus 5 end subscript equals T subscript 0 minus 5 end subscript$ , muss $T subscript 3 minus 5 end subscript equals T subscript 0 minus 5 end subscript to the power of negative 1 end exponent ring operator T subscript 3 minus 5 end subscript$ sein. Die berechnete Transformations-Matrix $T subscript 3 minus 5 end subscript$ enthält die letzten drei Gelenkwinkel, die nur noch von der T-Form auf Euler-Form gebracht werden müssen. Die Roboterwinkel $theta subscript 4$ und $theta subscript 5$ sind nicht dieselben wie $alpha$ und $beta$ .

Letztere werden im globalen Koordinatensystem angegeben, die Roboterwinkel $theta subscript 4$ und $theta subscript 5$ beziehen sich auf die Roboterposition.

$theta subscript 4 equals a tan open parentheses 2 asterisk times T subscript 0 minus 5 end subscript left square bracket 1 comma 0 right square bracket asterisk times T subscript 0 minus 5 end subscript left square bracket 0 comma 0 right square bracket close parentheses$

wobei $T subscript 0 minus 5 end subscript left square bracket 1 comma 0 right square bracket$ das erste Element (0) in der Reihe 1 bedeutet.

$theta subscript 5 equals a tan open parentheses 2 asterisk times left parenthesis negative T subscript 0 minus 5 end subscript left square bracket 2 comma 0 right square bracket asterisk times square root of T subscript 0 minus 5 end subscript left square bracket 2 comma 1 right square bracket squared plus T subscript 0 minus 5 end subscript left square bracket 2 comma 2 right square bracket squared end root close parentheses$