Startseite > Automotive > Assistenzsysteme > Lernen statt programmieren

Neuronale Netze für die Bilderkennung

Lernen statt programmieren

9. Mai 2016, 8:53 Uhr | Von Chris Rowen und Rishi Kumar

▶ Diesen Artikel anhören

Fortsetzung des Artikels von Teil 1

Einsatzgebiete von CNNs

CNNs werden in unterschiedlichsten Bereichen eingesetzt, beispielsweise zur Bild- und Mustererkennung, Spracherkennung, Verarbeitung von natürlicher Sprache und zur Videoanalyse. Es gibt mehrere Gründe, warum Convolutional Neuronal Networks immer wichtiger werden. In konventionellen Modellen für die Mustererkennung müssen die Merkmal-Extraktionswerkzeuge manuell entwickelt werden. In CNN werden sowohl die Gewichtung der Faltungsschichten für die Merkmal-Extraktion als auch die voll verbundenen Schichten für die Klassifikation erst während des Trainingsprozesses festgelegt. Die verbesserten Netzwerkstrukturen von CNNs führen zu geringeren Speicheranforderungen und ermöglichen gleichzeitig eine bessere Leistung bei Anwendungen, bei denen die Eingabe eine lokale Korrelation (etwa von Bildern und Sprache) aufweist.

Den hohen Anforderungen an die Berechnungsressourcen für das Training und die Evaluierung von CNNs werden beispielsweise GPUs, DSPs oder andere Halbleiterarchitekturen gerecht, die für einen hohen Durchsatz und einen geringen Energieverbrauch bei der Durchführung von CNN-Berechnungen optimiert sind. Konkret bietet etwa der für Bildverarbeitungs-Anwendungen entwickelte Tensilica-Vision-P5-DSP von Cadence genügend Berechnungs- und Speicher-Ressourcen für die Ausführung von CNNs mit hoher Effizienz. In Muster- und Bilderkennungsanwendungen werden die bestmöglichen fehlerfreien Erkennungsraten (Correct Detection Rates, CDRs) mit CNNs erreicht. Zum Beispiel erreichten CNNs bei der Erkennung von handschriftlichen Ziffern eine CDR von 99,77 %, bei 3D-Objekten eine CDR von 97,47 % sowie bei einem Test mit rund 5600 Bildern mit mehr als zehn Objekten eine CDR von 97,6 %. CNNs gewährleisten nicht nur die beste Leistung im Vergleich zu anderen Erkennungsalgorithmen, sie übertreffen sogar bei bestimmten Tests Menschen, beispielsweise bei der Klassifizierung von Objekten in fein unterteilten Kategorien, wie bei Hunderassen oder Vogelarten. Ein typischer Bildverarbeitungs-Algorithmus besteht aus vier Stufen: Aufbereitung des Bildes, Ermittlung der ROI-Bereiche (Regions of Interest), die wahrscheinlich Objekte enthalten, Objekterkennung und Entscheidungsfindung. Die Aufbereitung ist gewöhnlich von den Eingabe-Details abhängig – besonders vom Kamerasystem – und wird häufig von einer festverdrahteten Einheit außerhalb des Vision-Subsystems ausgeführt. Die Entscheidungsfindung am Ende der Pipeline erfolgt normalerweise auf der Basis von erkannten Objekten. Diese Entscheidungen stellen gewöhnlich keine besonders rechen- oder speicherintensiven Probleme dar. Die große Herausforderung liegt in den Objektfindungs- und Erkennungsstufen, wo CNNs mittlerweile eine große Bedeutung haben.

CNN-Schichten

Durch die Überlagerung mehrerer und verschiedener Schichten in einem CNN lassen sich komplexe Architekturen für die Klassifizierung von Problemen realisieren. Vier Typen von Schichten sind am häufigsten: Faltungsschichten, Pooling-/Subsampling-Schichten, nichtlineare Schichten und vollständig verknüpfte Schichten (Fully Connected Layer).

Jobangebote+ passend zum Thema

Regional Key Account (m/w/d) für Elektronische Bauteile

KOA Europe GmbH, Dägeling

Alle Jobangebote im Elektroniknet Karrierebereich anzeigen

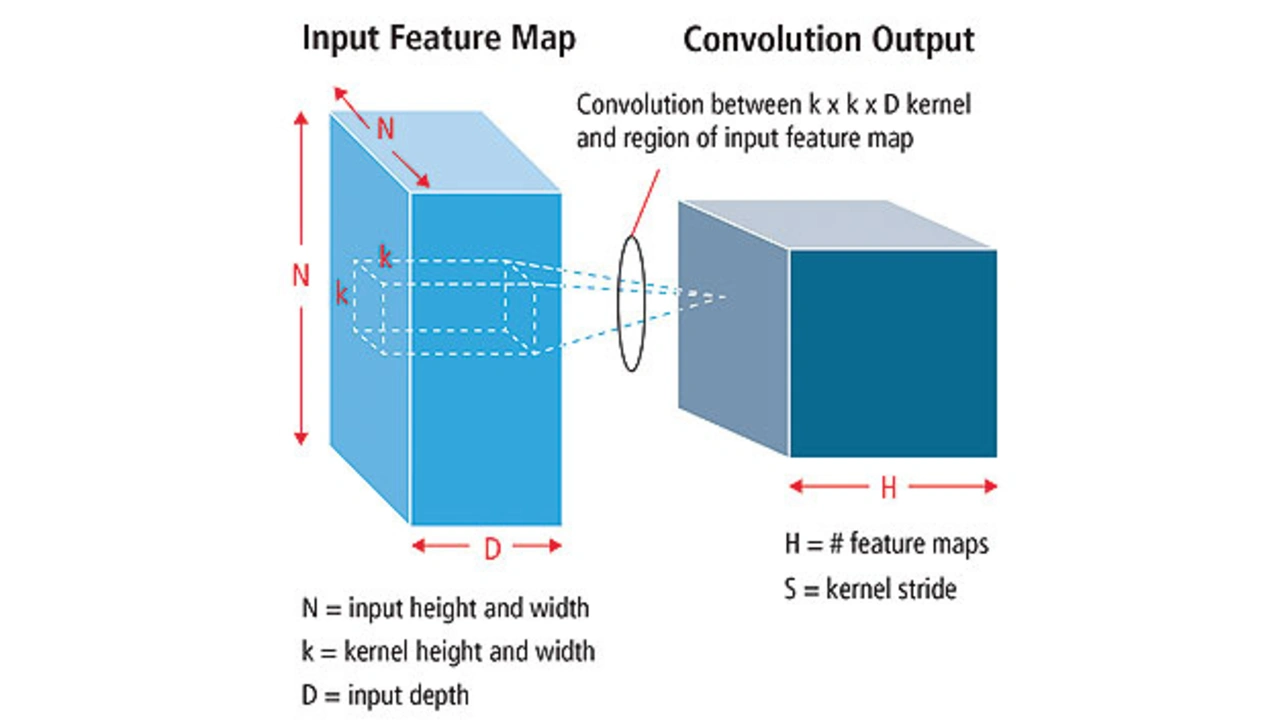
Faltungsebenen

Die Faltungsoperation extrahiert verschiedene Merkmale der Eingabe. Die erste Faltungsebene extrahiert einfache Merkmale wie Kanten, Linien und Ecken. Höhere Ebenen extrahieren komplexere Merkmale. Bild 5 illustriert den Prozess der 3D-Faltung in CNNs. Die Eingabe hat die Größe N × N × D und wird mit H Kernen gefaltet, wobei jeder eine Größe von k × k × D aufweist. Die Faltung einer Eingabe mit einem Kern produziert ein einzelnes Ausgabe-Merkmal, während H Kerne entsprechend H unabhängige Merkmale produzieren.

Beginnend in der oberen linken Ecke der Eingabe wird jeder Kern von links nach rechts bewegt, jeweils um ein Element. Sobald die obere rechte Ecke erreicht wird, wird der Kern ein Element nach unten bewegt, und wieder wird der Kern von links nach rechts, immer um jeweils ein Element bewegt. Dieser Prozess wird solange wiederholt, bis der Kern die untere rechte Ecke erreicht. Im Fall von N = 32 und k = 5 sind dies 28 unterschiedliche Positionen von links bis rechts und 28 unterschiedliche Positionen von oben bis unten, die der Kern einnehmen kann. Entsprechend diesen Positionen enthält jedes Merkmal in der Ausgabe 28 · 28 (d. h. (N–k+1) · (N–k+1)) Elemente. Für jede Position des Kerns in einem gleitenden Fensterprozess werden k · k · D Eingabe-Elemente und k · k · D Kernelemente jeweils Element für Element multipliziert und akkumuliert. Um ein Element eines Ausgabe-Merkmals zu erstellen, sind k · k · D Multiplizier- und Akkumulier-Operationen erforderlich.

Pooling-/Subsampling-Schichten

Die Pooling-/Subsampling-Schicht reduziert die Auflösung der Merkmale. Dies macht die Merkmale robust gegenüber Rauschen und Verzerrungen. Es gibt zwei Arten von Pooling: Maximal-Pooling und Mittelwert-Pooling. In beiden Fällen wird die Eingabe in nichtüberlappende zweidimensionale Bereiche geteilt. In Bild 4 ist zum Beispiel die Schicht 2 die Pooling-Ebene. Jedes Eingabe-Merkmal ist 28 × 28 groß und wird in 14 × 14 große Bereiche der Größe 2 × 2 geteilt.

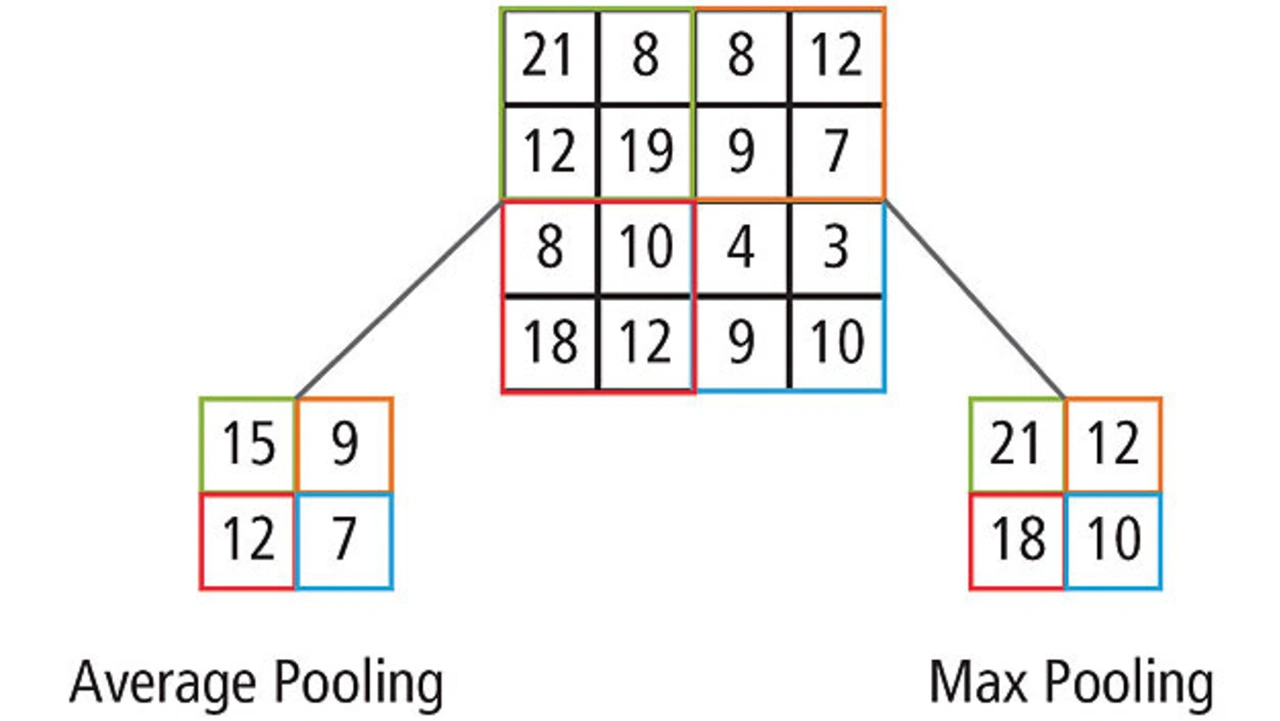
Für ein Mittelwert-Pooling wird der Mittelwert der vier Werte im Bereich berechnet. Für ein Maximal-Pooling wird der maximale Wert der vier Werte ausgewählt.

Bild 6 verdeutlicht den Pooling-Prozess weiter. Die Eingabe hat die Größe 4 × 4. Für ein 2×2-Subsampling wird ein 4×4-Bild in vier nicht überlappende Matrizen der Größe 2 × 2 aufgeteilt. Im Falle eines Max-Pooling ist der maximale Wert der vier Werte in der 2×2-Matrix die Ausgabe. Im Falle eines Mittelwert-Pooling ist der Mittelwert der vier Werte die Ausgabe. Ist das Ergebnis der Mittelwertbildung eine Bruchzahl, wird auf die nächste ganze Zahl gerundet.