Zukunft der Bauelemente
Chips 2020 – von der Nano- zur Femtoelektronik
Fortsetzung des Artikels von Teil 1
Von Nanometer zu Femtojoule
Wenn die weitere Transistorverkleinerung keine Kosten- und Funktionsvorteile mehr bringt, müssen wir nach neuen Antworten suchen auf die Frage: Wie können wir die anhaltend hohen Erwartungen an die Nano-Chips erfüllen? Im Grunde war die Erwartung schon immer die gleiche: Mehr Funktionalität bei reduzierten Kosten. Die Verkleinerung der Transistoren hat dies lange als das beste Mittel bedient. Nun braucht man neue Wege zu mehr Funktionalität und sinkenden Kosten, d.h. spezifizierte Aufgaben mit minimalem Aufwand (z.B. Transistorzahl) schnell und mit minimalem Energieverbrauch erledigen.
Jobangebote+ passend zum Thema
![Energie und Rechenleistung digitaler Multiplizierer und Addierer. [A]=[5], [E]=[6], [F]=[3], [G]=[4]. Energie und Rechenleistung digitaler Multiplizierer und Addierer. [A]=[5], [E]=[6], [F]=[3], [G]=[4].](https://cdn.elektroniknet.de/thumbs/media_uploads/images/1340706519-39-chips-2020-bild-3.jpg.1280x0.webp)
Als ein besonders transistor- und energiehungriges Modul gelten digitale n-bit- × n-bit-Multiplizierer, die Herzstücke aller Prozessoren sind und besonders in der Verarbeitung von Bildern, Video und Grafik ein Drittel der gesamten Energie benötigen.
Bild 3 zeigt die Zahl der Multiplikationen je Sekunde (OPS) und die Energie je Multiplikation in Joule (J=Ws) bzw. deren Kehrwert, die Energieeffizienz in GOPS/mW. Die Kurven 3 und 4 zeigen neueste Ergebnisse von der ISSCC 2012 (International Solid-State Circuits Conference), hier insbesondere jeweils für zwei Versorgungsspannungen.
Der Energiebedarf nimmt jeweils etwa mit U² ab, was das häufig benutzte Modell bestätigt, dass die Energie ~CU² ist. Man sieht aber auch, dass die Geschwindigkeit entsprechend abnimmt und man für einen bestimmten Durchsatz von Multiplikationen bei niedriger Spannung nun entsprechend mehr Multiplizierer parallel betreiben müsste (40 im Beispiel 3 von Intel).
Deshalb sind in dieses Bild auch Geraden für den gleichen Gütefaktor (figure of merit) eingetragen, nämlich die Zahl der Multiplikationen je Sekunde in GOPS für ein Energie-Budget von 1 pJ. Die beiden Beispiele 3 und 4 in Standard-CMOS-Logik zeigen, dass allein das Absenken der Spannung mit einem unakzeptablen Verlust der Rechenleistung verbunden ist.
Für die gewünschten niedrigen Spannungen muss also eine angepasste Schaltungstechnik entwickelt werden. Dies muss eine differenzielle Schaltungstechnik sein, um trotz der Transistor-Varianz (vorhergehender Abschnitt) und trotz Störungen Übergänge sowie Pegel zu sichern und – das ist das wichtigste – die Geschwindigkeit der Übergänge in beiden Richtungen zu beschleunigen.
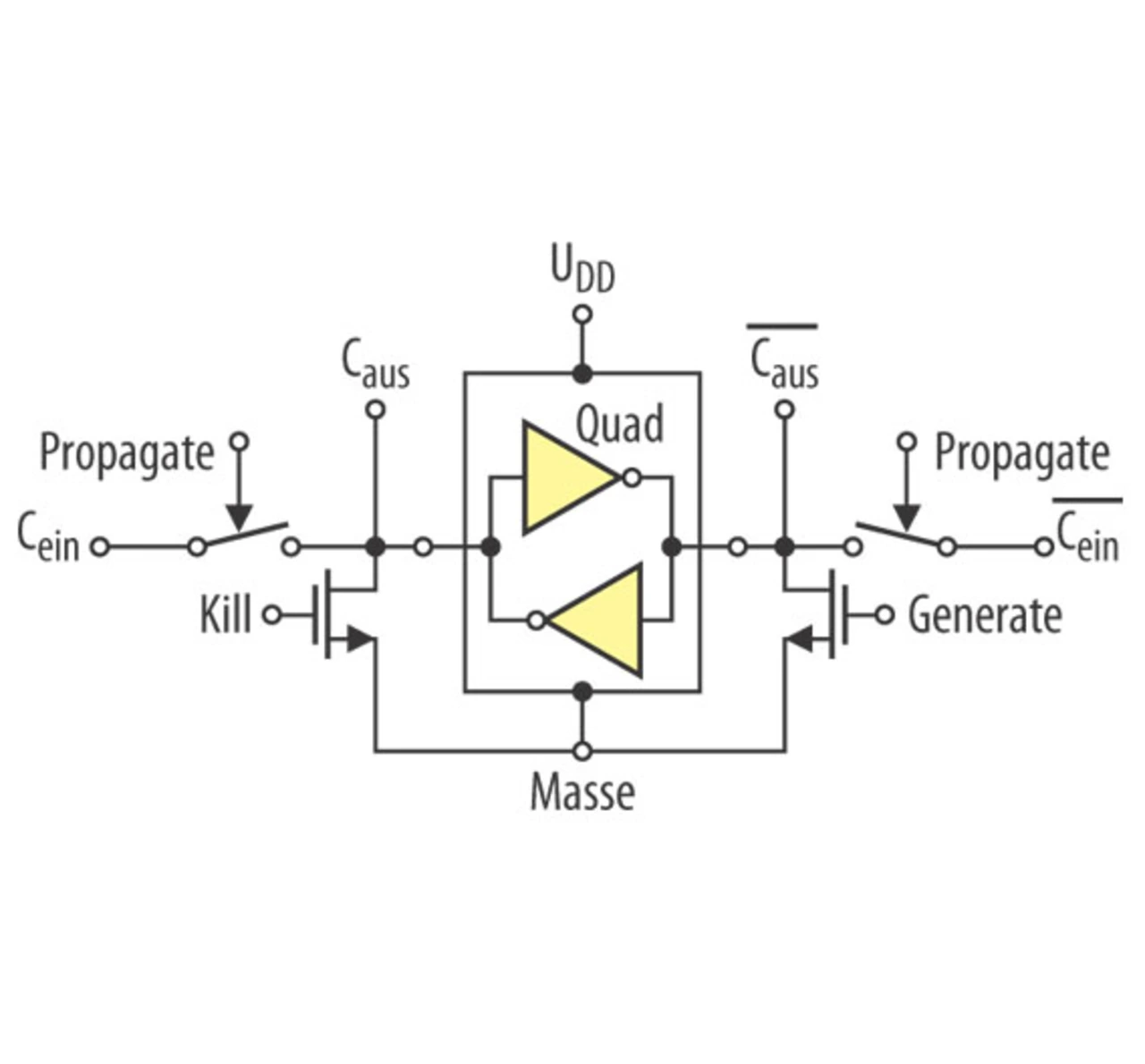
Als der bisher beste Treiber an den Gatterausgängen hat sich das kreuzgekoppelte, komplementäre Inverter-Paar erwiesen, wie es prinzipiell in Bild 4 dargestellt ist. Es zeigt eine Stufe einer sog. Manchester-Carry-Chain, der schnellsten Schaltung für den Transport der Überträge in einem Addierer.
Die differenzielle Schaltungstechnik hat an sich eine prominente Geschichte, was Störsicherheit und Geschwindigkeit betrifft, beginnend mit ECL (Emitter-Coupled-Bipolar-Logik) und dann in MOS-Technik mit DCVSL (Differential-Cascode-Voltage-Switched-Logik). In [5] werden Daten für den Schaltungstyp gemäß Bild 4, auch HIPERLOGIC genannt, dargestellt und erläutert.
In [6] wird mit einer Erweiterung dieses Schaltungstyps ein 64-bit-Addierer in 180-nm-Technologie mit der beachtlichen Energie von nur 170 fJ je Operation bei einem Durchsatz von 58 MOPS beschrieben. Diese Daten sind unter [6] in Bild 5 eingetragen.
In der Komplexität vergleichbar mit den Multiplizierern [3,4], markiert der Addierer in differenzieller Technik eine Verbesserung um eine Größenordnung in Energie und Durchsatz-Gütefaktor, obwohl er auf der Nanometer-Skala mit 180 nm um mehr als drei Technologiegenerationen gegenüber den 45/32-nm-Multiplizierern zurückliegt.
Transistor-Effizienz
Zur Zukunft energieeffizienter Nanochips gehört auch, dass aufgabenbezogen deren Schaltungseffizienz, d.h. u.a. ihre Transistor-Effizienz, unter die Lupe genommen wird. Die Multiplizierer sind ein markantes Beispiel: Herkömmlich und entsprechend den IEEE-Standards 754 wird, wie auch im Schulrechnen, wegen der Überträge mit den letzten Stellen (LSB's = Least Significant Bits) begonnen. Es dauert lange, bis die wichtige führende Stelle des Produkts ermittelt ist, die Transistorzahl wächst quadratisch mit der Wortlänge n der Multiplikanden.
Tabelle 1 zeigt, dass z.Zt. schon ein 8-bit- × 8-bit-Multiplizierer 1.600 Transistoren benötigt und diese Zahl bei 24 bit × 24 bit auf 14.400 steigt.
| Wortlänge in bit | 8 | 16 | 24 | 54 |
|---|---|---|---|---|
| Standard-LSB | 1.600 | 6.400 | 14.400 | 77.000 |
| DIGILOG 6 bit Genauigkeit | 540 | 1.030 | 1.620 | - |
| DIGILOG 10 bit Genauigkeit | - | 2.100 | 2.700 | 7.000 |
Tabelle 1. Transistorzahl von n-bit- × n-bit-Multiplizierern.
Bei allen natürlichen und technischen Aufgaben haben wir es mit Eingangs- und Ausgangsdaten zu tun, die u.U. hohe Dynamik haben (das Auge sieht einen Helligkeitsbereich bis zu 100 Mio. zu 1, entsprechend 24 bit), während bei jedem aktuellen Helligkeitswert die relative Genauigkeit im Prozentbereich (Helligkeitsempfindlichkeit des Auges 1 % entsprechend 7 bit) bis zu 0,01 %=10 bit liegt. Die Natur und wir sind also bei allen Multiplikationen an der Höhe des Ergebnisses und an den führenden 6 bis 10 bit interessiert.
Dass das Verhältnis der Empfindlichkeit bzw. Genauigkeit dN zum aktuellen Wert N einer Größe, dN/N, konstant ist, erinnert an das Webersche Gesetz über Größen in der Natur: Hören und Sehen funktionieren so. Was würde man gewinnen, wenn man naturnahe und technische Daten, z.B. Sensordaten und ihre Gewichtsfaktoren, so in Multiplizierern verarbeitet, dass mit den führenden Einsen begonnen wird? Wenn im Multiplikanden A die führende Eins den Wert 2j und im Multiplikanden B den Wert 2k hat, dann gilt:
A = 2j + AR,j-1
B = 2k + BR,k-1,
und die Multiplikation der beiden ergibt:
A × B= 2j × B + 2k × AR,j-1 + AR,j-1 × BR,k-1
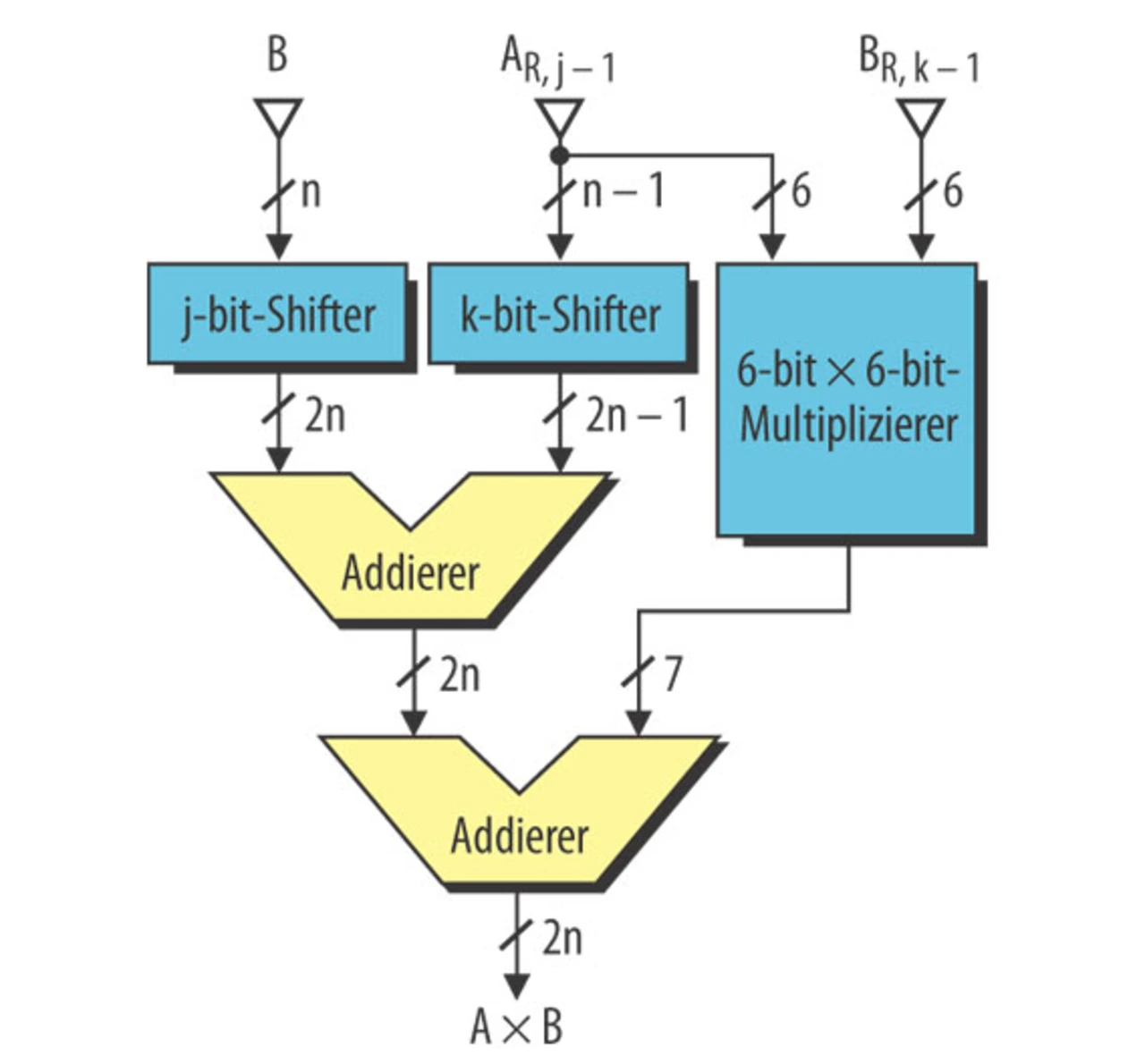
Mit Schieben und Addieren hat man sofort ein größenordnungsmäßiges Ergebnis. Parallel dazu multipliziert man die Reste (z.B. 6 bit oder 10 bit lang, ggf. auf die konventionelle Art) und erhält ein 6 bit oder 10 bit genaues Ergebnis (Bild 5).
Die Transistorzahl ist dramatisch um Faktoren 6 bis 11 reduziert (Tabelle 1) und die Geschwindigkeit dreimal höher und mehr, wenn z.B. am Ausgang nur n bit weiter verarbeitet werden. Wir haben solche Multiplizierer wegen ihrer quasi-logarithmischen Darstellung von A und B als DIGILOG-Multiplizierer 1991 erstmals veröffentlicht und Ergebnisse in HIPERLOG-Technik von 2000 sowie die Projektion in 20-nm-Technologie für 2020 [5] in Bild 3 eingetragen. Danach würde z.B. ein 16-bit- × 16-bit-Multiplizierer 2020 nur 1 fJ je Multiplikation benötigen, etwa ein Tausendstel der Energie in den Publikationen [3] und [4].
Dieser markante Fortschritt kann in allen Systemen zum Tragen kommen, die Bilder-, Video-, Grafik-intensiv sind und z.B. in Spielen, Multimedia und Robotik eingesetzt werden. Hier ist auch der Speicher- und Kommunikationsbedarf sehr hoch, wozu die folgenden Abschnitte Aussagen machen.
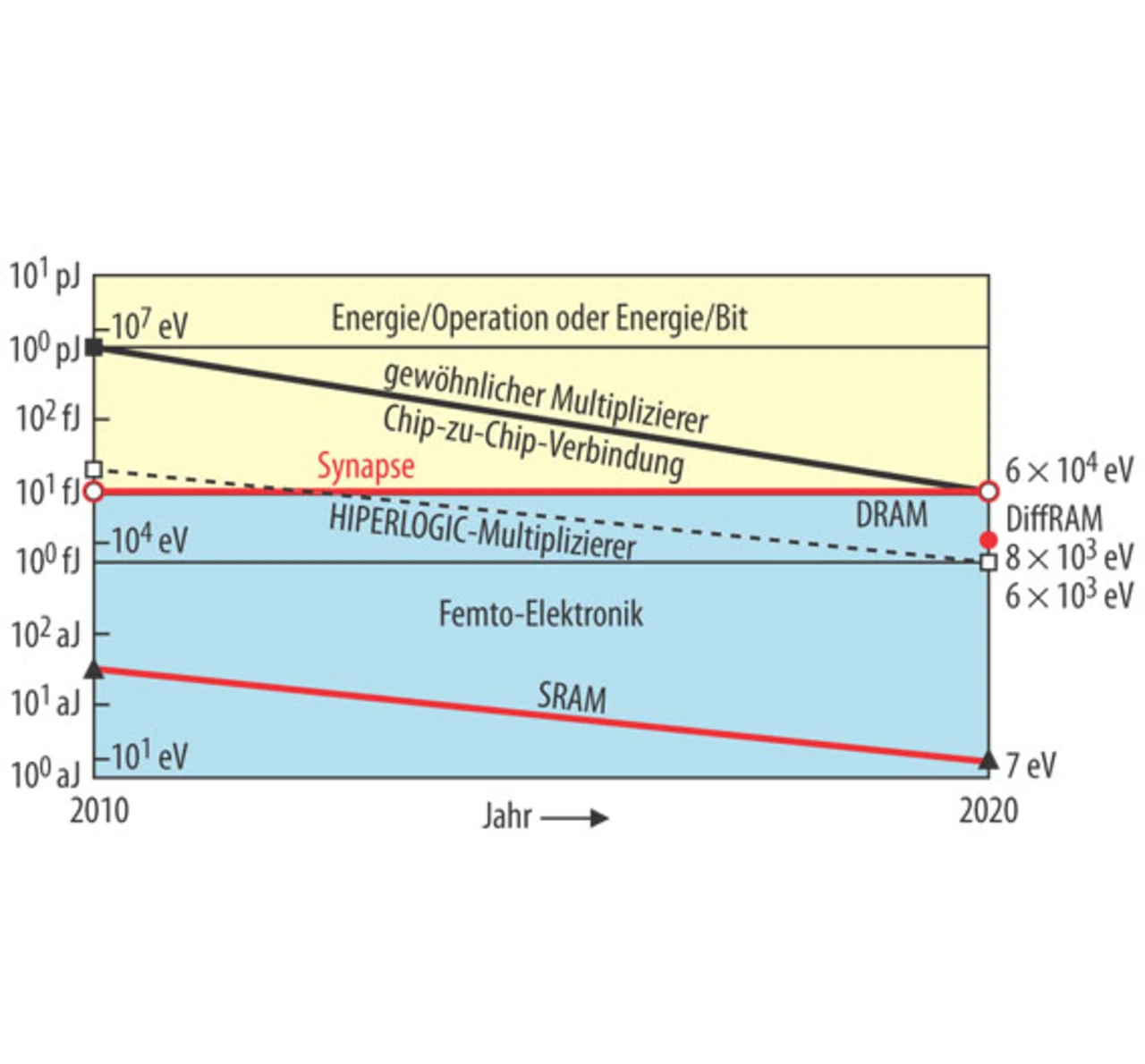
Bild 6 zeigt die Prognosen der Energie je Multiplikation für konventionelle und HIPERLOGIC-Multiplizierer bis 2020 zusammen mit denen der anderen kritischen Aufgaben: Speicher und Chip-Chip-Verbindung.
Das Niveau von 10 fJ ist besonders markiert: Es ist die Energie, die eine Synapse im Gehirn benötigt, wenn sie ein Aktionspotenzial von 70 mV mit der Umladung von ca. 500.000 Ionen auslöst. Der Bereich unterhalb von 10 fJ wurde Femtoelektronik genannt.
- Chips 2020 – von der Nano- zur Femtoelektronik
- Von Nanometer zu Femtojoule
- Speicher-Chips
- Die dritte Dimension
- Literatur und Autor