Regelungstechnik – Teil 1 von 6
Stabilität von Netzteilen
Nur ein zuverlässiges Netzteil garantiert eine störungsfreie Stromversorgung. Doch worauf muss dabei geachtet werden? Der erste Teil der Artikelserie von Omicron Lab behandelt die Grundlagen der Stabilitätsanalyse im Frequenzbereich und erklärt, wie ein Bode-Diagramm erstellt wird.
Bestimmt haben viele Studenten in Vorlesungen zur Regelungstechnik so einiges über den Entwurf von Regelkreisen gehört – auch, dass die Auslegung im Frequenzbereich dafür am besten geeignet ist. Doch vermutlich durfte kaum jemand diese Methode direkt an Netzteilen anwenden. Kein Wunder also, dass für viele der Begriff »Regelungstechnik« abschreckend klingt. Doch Regelungstechnik kann auch einfach und unterhaltsam erklärt werden, allerdings darf dabei der Bezug zur Praxis nicht fehlen.
Genau diesen Schritt geht Omicron Lab mit der Serie von Fachartikeln »Regelung von Schaltnetzteilen – Schritt für Schritt«. Der erste Beitrag geht auf reale Netzteile ein und bringt besonders die Begriffe Frequenzbereichs-analyse, Bode-Diagramm, Amplitudenreserve, Phasenreserve, Durchtrittsfrequenz und Netzteil-Stabilitätskriterien näher. Doch warum sind diese Themen bei der Gestaltung stabiler Netzteile in der Praxis überhaupt von Bedeutung?
Auslegung im Frequenzbereich

Was bedeutet »Auslegung im Frequenzbereich« und warum ist der Frequenzbereich besser geeignet als der Zeitbereich? Der Frequenzbereich vermittelt mehr Informationen über die Stabilität der Netzteile als eine einfache Sprungantwort. Im Zeitbereich – das heißt, wenn die Belastung des Netzteils sprunghaft gewechselt und das Einschwingverhalten betrachtet wird – ist nie ganz sicher, warum und wie weit man von einer Instabilität entfernt ist.
Bei der Frequenzbereichsanalyse wird ein Sinus mit einer bestimmten Frequenz, zum Beispiel 10 Hz, in das Netzteil eingespeist. Anschließend wird gemessen, wie sich das Signal beim Durchlaufen des Netzteils bis zum Ausgang hin verändert. Nach dem Einspeisen kann die Sinuswelle am Eingang des Netzteils mit jener am Ausgang verglichen werden. Wichtig ist der Amplitudenunterschied zwischen den beiden Sinuswellen (Verstärkung) und die »Phasenverschiebung«. Wird beispielsweise eine 1-V-Sinuswelle in das System eingespeist und am Ausgang eine 10-V-Sinuswelle beobachtet, dann beträgt die Verstärkung 20 dB:
Wenn bei 10 Hz die Sinuswelle am Ausgang um 90° hinter der eingespeisten Sinuswelle nacheilt, beträgt die Phase bei 10 Hz -90°. Nun können im Bode-Diagramm bei 10 Hz zwei Punkte eingezeichnet werden. Einer im Amplitudengang und einer im Phasengang. Dieser Vorgang wird zum Beispiel bei 20 Hz, 50 Hz, 100 Hz und so weiter wiederholt, bis das Bode-Diagramm bis zur halben Schaltfrequenz erstellt ist.
Der ermittelte Amplituden- und Phasengang entspricht dem Bode-Diagramm des Netzteils mit offenem Regelkreis vor der Kompensation. Angenommen wird, dass ein einfacher Proportionalregler mit einer Verstärkung von 1 zum Einsatz kommt.
Doch worauf ist in einem Bode-Diagramm zu achten und wie soll das Bode-Diagramm eines stabilen Netzteils aussehen?
Stabilitätskriterien im Bode-Diagramm
Die Interpretation von Bode-Diagrammen bezüglich der Stabilität ist im Grunde einfach. Vier Attribute sind dabei beachtenswert:
- Durchtrittsfrequenz Fx
- Phasenreserve Pm
- Amplitudenreserve Gm
- Steigung des Amplitudengangs bei der Durchtrittsfrequenz
Diese Attribute verraten fast alles, was für die Stabilität des Netzteils wichtig ist.
Durchtrittsfrequenz.
Die Durchtrittsfrequenz zeigt, wie schnell sich das Netzteil nach einem sprunghaften Lastwechsel erholt. Je höher sie ist, desto schneller fällt die Sprungantwort im Zeitbereich aus. Sie muss auch bekannt sein, um die Phasenreserve zu ermitteln.
Die Durchtrittsfrequenz ist definiert als jene Frequenz, bei der der Amplitudengang die 0-dB-Achse schneidet. Aber was bedeutet das eigentlich? Zur Erinnerung: Eingespeist werden Sinuswellen verschiedener Frequenzen, anschließend werden deren Verstärkung gemessen und in dB graphisch dargestellt. Wird zum Beispiel eine 1-V-Sinuswelle in das System eingespeist und am Ausgang eine Sinuswelle mit exakt gleicher Amplitude beobachtet, liegt eine Verstärkung von 1 vor, was in dB ausgedrückt einem Wert von 0 entspricht, wie in der folgenden Gleichung dargestellt:
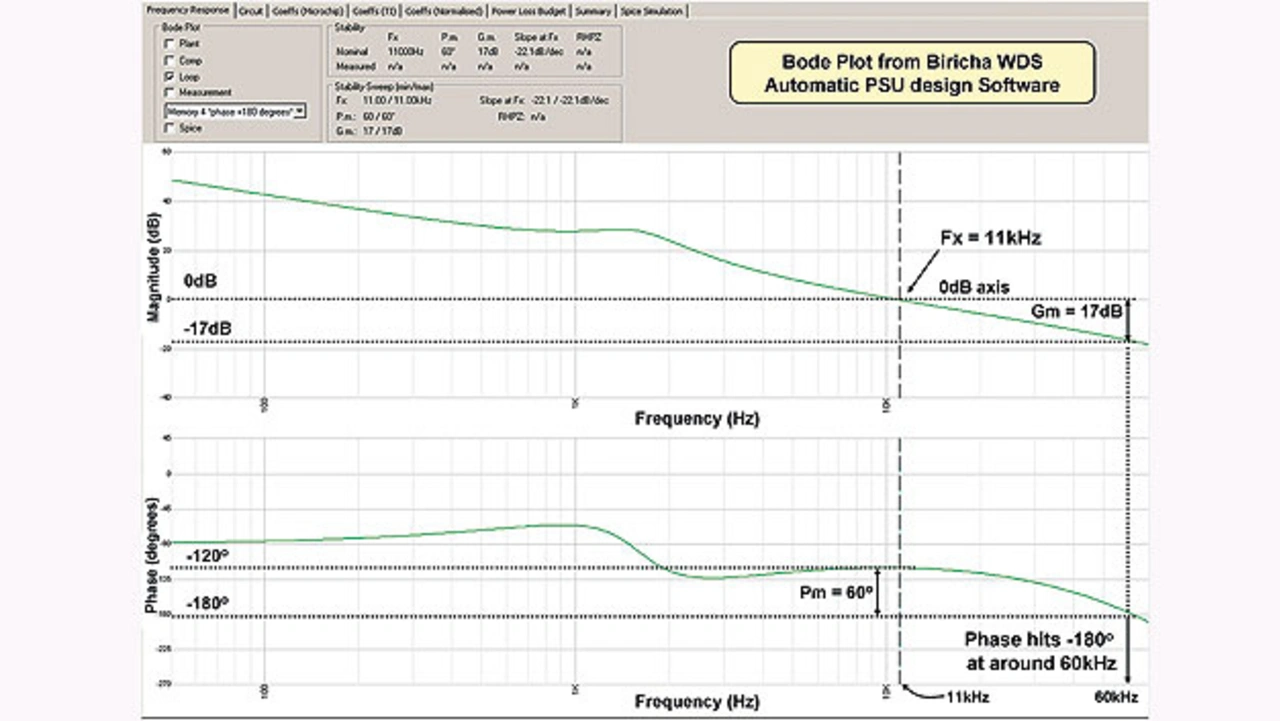
In Bild 1 ist das Bode-Diagramm eines einfachen Abwärtswandlers dargestellt. Ein Blick auf den Amplitudengang zeigt, dass bei etwa 11 kHz die Verstärkung 0 dB beträgt. Die Durchtrittsfrequenz für dieses spezielle Netzteil beträgt also 11 kHz. Für das vorliegende Netzteil beträgt die Schaltfrequenz 200 kHz. Für einen stabilen, robusten Betrieb und ein realistisches Entwicklungsziel sollte die Durchtrittsfrequenz maximal ein Zehntel der Schaltfrequenz betragen.
Phasenreserve
Nachdem die Durchtrittsfrequenz bestimmt wurde, lässt sich die Phasenreserve ermitteln. Sie ist das womöglich wichtigste Attribut zur Gewährleistung der Stabilität. Die Phasenreserve ist ein Maß für die Dämpfung und Schwingneigung des Netzteils. Sie ist definiert als der Betrag, um den die Phasenverzögerung bei der Durchtrittsfrequenz über -180° liegt. Das Bode-Diagramm in Bild 1 zeigt, dass die Durchtrittsfrequenz 11 kHz beträgt. Die Phase bei 11 kHz beträgt etwa -120°. Das Minuszeichen bedeutet, dass die Sinuswelle am Ausgang der injizierten Sinuswelle um 120° nacheilt. Wie viel liegt die Phase nun über -180°? Die Antwort: 180° - 120° = 60°.
Es gilt: Mit abnehmender Phasenreserve wird das Systemverhalten immer oszillatorischer. Beträgt die Phasenreserve 0°, dann handelt es sich um einen perfekten Oszillator, der in der Ingenieurwissenschaft als instabil bezeichnet wird. Um auf Nummer sicher zu gehen, ist bei der Phase ein gewisser »Sicherheitsabstand« gewünscht, um Oszillationen zu vermeiden. Der Wert ist als Phasenreserve bekannt – für die selbst unter ungünstigsten Bedingungen mindestens 45° angestrebt werden sollten. Noch besser ist ein Wert von 55° bis 60°.
Amplitudenreserve
Ähnlich wie die Phasenreserve ist die Amplitudenreserve ein Maß für die Stabilität. Beim Betrachten des Phasengangs erkennt man, dass die Phase bei einer gewissen Frequenz einen Wert von -180° erreicht. Die Verstärkung bei genau dieser Frequenz entspricht der Amplitudenreserve. In unserem Fall erreicht die Phase in der Simulation den Wert von -180° bei etwa 60 kHz. Bei 60 kHz liegt die Verstärkung etwa 17 dB unter Null. Die Amplitudenreserve beträgt somit 17 dB. Auch hier gilt: Wenn sich die Amplitudenreserve 0 dB nähert, beginnt das Netzteil zu oszillieren. Für ein robustes Netzteil ist eine Amplitudenreserve von mindestens 10 dB wünschenswert: Die Verstärkung muss 10 dB unter Null liegen, wenn die Phase -180° erreicht.
Steigung des Amplitudengangs
Das vierte Teilstück des Stabilitätspuzzles lässt sich bestimmen, indem man den Anstieg des Amplitudengangs bei der Durchtrittsfrequenz betrachtet. Für ein robustes und stabiles System ist idealerweise ein flacher Anstieg im Bereich der Durchtrittsfrequenz von etwa -20 dB pro Dekade wünschenswert. Unter »Dekade« versteht man in diesem Zusammenhang eine Frequenzänderung um den Faktor 10. Wenn zum Beispiel die Verstärkung bei 5 kHz 20 dB beträgt, dann sollte die Verstärkung bei einer 10-mal höheren Frequenz – also 50 kHz – höchstens um 20 dB abgefallen sein. Eine steile Steigung im Bereich der Durchtrittsfrequenz könnte das Netzteil gefährlich nahe an die Instabilität bringen. Aus dem Bode-Diagramm ist ersichtlich, dass der Anstieg etwa -22 dB pro Dekade beträgt.
- Stabilität von Netzteilen
- Praxisbeispiel
- Die Autoren

