Methodisch vorgehen
Digitale Sicherheitsmechanismen in kritischen Systemen
ISO-26262-konforme elektronische Automotive-Systeme zu entwickeln, die gleichzeitig platzsparend sind, ist eine der größten Herausforderungen im Automotive-Bereich. Eine strukturelle, skalierbare und flexible Methodik stellt hierbei einen sinnvollen Ansatz dar.
Elektronische Kontrollsysteme (Electronic Control System, ECS), die in heutige Fahrzeuge integriert sind, werden immer zahlreicher und komplexer. Obwohl moderne Halbleitertechnologien sehr zuverlässig sind, wird die Wahrscheinlichkeit des Auftretens eines Fehlers in einem der elektronischen Systeme des Fahrzeugs als hoch angesehen. Abhängig davon, in welchem System ein solcher Plausibilitätsfehler auftritt, könnte das Leben des Fahrers oder der Mitfahrer gefährdet sein.
Um dieses Risiko zu bewerten, zu vermeiden bzw. zu mindern, hat die Automobilindustrie den elektrischen/elektronischen (E/E) FuSa-Standard IEC 61508 entwickelt und einen spezifischen FuSa-Standard für die Automobilindustrie mit ISO 26262 geschaffen [1] [2] [3] [4] [5].
Infolgedessen wurden das Automotive Safety Integrity Level (ASIL) [1] eingeführt und spezifische Anforderungen an neue Produkte gestellt, sowohl für den Entwicklungszyklus als auch für die Diagnosefunktionen in Bezug auf plausible zufällige Ausfälle. Zur Quantifizierung letzterer wurden verschiedene Hardware-Metriken eingeführt, da diese vom ASIL-Ziel des Produkts abhängen.
Für ASIL-C- und D-Anwendungen liegen die erforderlichen Single Point Fault Metrics (SPFM) bei 97 % bzw. bei 99 %, da fast jeder Fehler zu einer Verletzung des Sicherheitsziels (Safety Goal, SG) führen kann und daher mit hoher Diagnoseabdeckung erkannt werden muss. Das Erreichen der strengen Anforderungen an die Probabilistic Metric for Random Hardware Failures (PMHF) könnte auch für ein kompliziertes System, in dem vorübergehende Fehler berücksichtigt werden, eine Herausforderung darstellen.
Darüber hinaus sind Systemanalysen [1] [4] bei komplexen IC-Designs möglicherweise nicht vor dem Designstart abgeschlossen. Ohne das Ergebnis dieser Analysen können IC-Entwickler gegebenenfalls zu Beginn keine ordnungsgemäße Fehlererkennungslogik implementieren, sondern womöglich erst in sehr späten Phasen des Projekts. In diesen Fällen sollte die vorgeschlagene Methodik vollständig im digitalen Design durchgesetzt werden.
Wenn die Analysen abgeschlossen sind und alle FuSa-bezogenen Funktionen identifiziert sind, lassen sich die bereits implementierten SMs überarbeiten, aktualisieren oder sogar entfernen, wenn ein bestimmter Block von einem anderen SM abgedeckt wird. Der einfachste und unkomplizierteste Ansatz zur Erkennung von Fehlern in der digitalen Logik ist, Redundanz einzusetzen.
Dies wird im aktuellen Artikel nicht bewertet, da dies zwar einfach zu implementieren, jedoch in Bezug auf die Fläche ziemlich teuer ist (Logik muss verdoppelt oder verdreifacht werden und Vergleichslogik ist erforderlich). Wenn die Redundanz als SM genutzt wird, sollten die Fehlerauswirkungen der Ursache in der Dependent Failure Analysis [4] im Design berücksichtigt werden.
Der vorliegende Artikel konzentriert sich auf SMs, die sich überall in allen Arten von digitalen Designs einsetzen lassen. Die vorgeschlagene Methodik kann ganz oder teilweise auf Basis der FuSa-Analyse sowie technischer bzw. Hardware-Sicherheitsanforderungen angewendet werden. Die beschriebenen Techniken kommen bei der RTL-Codierung zum Einsatz, sind also technologieunabhängig.
Jobangebote+ passend zum Thema
Kategorisierung digitaler Entwicklung
Im Allgemeinen lässt sich digitale Logik in zwei Hauptklassen unterteilen – sequenziell und kombinatorisch. Die Hauptkategorisierung wird in der vorgeschlagenen Methodik noch erweitert. Die zusätzliche Kategorie wird für die FSM-Logik (Finite State Machine) verfeinert:
➔ FSM-Zustands-/Übergangslogik: kombinatorische und sequenzielle Logik, die sich nur auf FSM bezieht.
➔ Gemeinsame sequenzielle Logik: alle Register oder Latches, die nicht mit der FSM-Logik zusammenhängen.
➔ Gemeinsame kombinatorische Logik: alle Varianten von kombinatorischer Logik, die nicht mit FSM zusammenhängen.
Die neu eingeführte Kategorisierung ist erforderlich, da verschiedene SMs vorgeschlagen werden, die unabhängig voneinander angewendet werden können.
Aus Sicht der FuSa lässt sich die digitale Logik aufteilen in:
➔ Hauptfunktionslogik: Fehlermodi in dieser Logik könnten direkt zu einer Verletzung des SG führen oder mit anderen Worten, das Potenzial haben, das Sicherheitsziel (PVSG, Probability of Violation of Safety Goal) direkt zu verletzen.
➔ Fehlererkennungslogik: Fehlermodi in dieser Logik könnten nur indirekt gegen das SG verstoßen (in der Regel in Kombination mit einem Fehler in der Hauptfunktionslogik). Diese Logik implementiert selbst Sicherheitsmechanismen oder eine andere Logik, die das SG nicht direkt verletzen kann (z. B. DFT, Design For Test).
Fehlererkennungstechniken
Fehlererkennung von endlichen Zustandsautomaten
Abhängig von den ASIL-Anforderungen kann es erforderlich sein, bis zu 3-Bit-Fehler zu erkennen und in einigen Fällen bis zu 2-Bit-Fehler zu korrigieren. Die Zustände der endlichen Zustandsautomaten (FSM) sind mit 2 oder 3 Bit Hamming Distance (HD) codiert, die die Erkennung von bis zu ein oder zwei fehlerhaften Bits ermöglicht. Das Wesentliche an den vorgeschlagenen SMs ist die Verwendung ordnungsgemäß codierter Zustandswerte und die Umwidmung des Standard-FSM-Zustands.
Die erforderliche HD zwischen den Zuständen kann mit einer weithin bekannten Hot/Cold-Codierung 0 [7] erreicht werden. Diese Codes sind flächenmäßig ziemlich teuer – die Anzahl der benötigten Register entspricht der Anzahl der Zustände. Für den gleichen Zweck werden Paritäts- und Fehlerkorrekturcodes (ECC, Elliptic Curve Cryptography) für Zustandsaufzählungswerte genutzt, da sie effizienter und kostengünstiger sind.
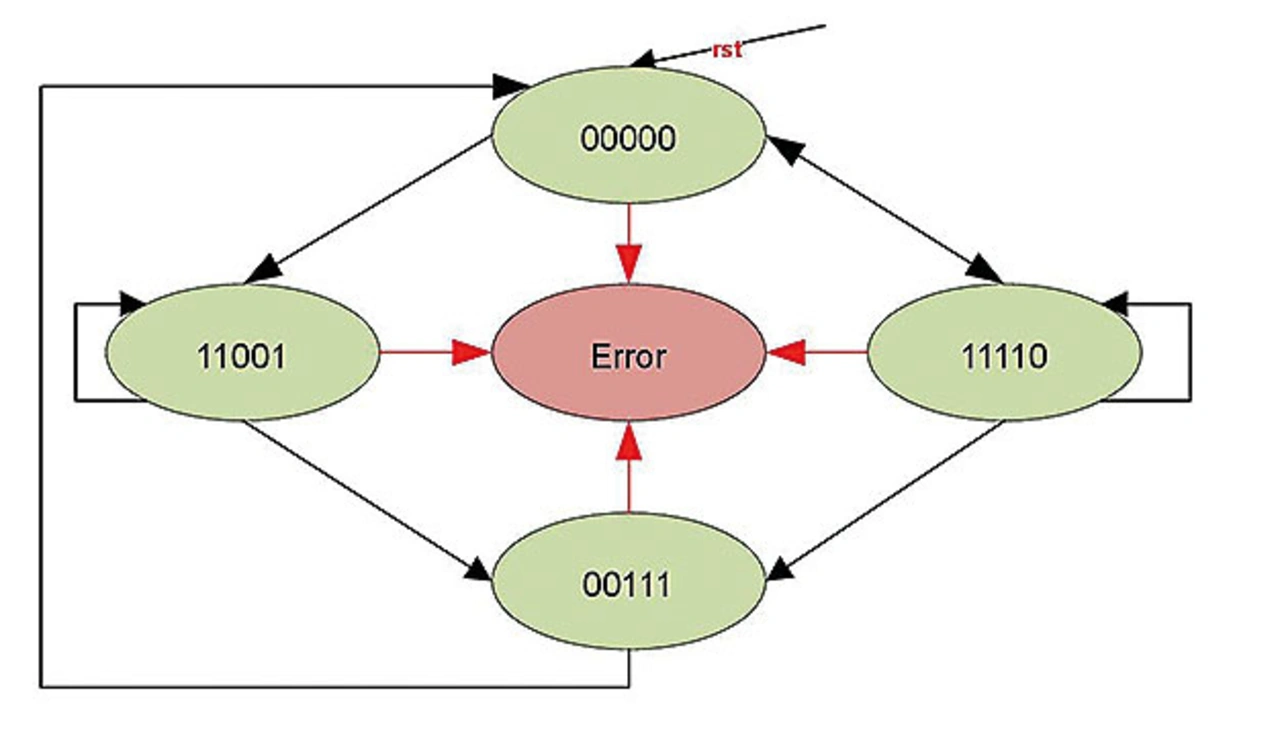
Der Fehlerstatus in der RTL (Register-Transfer Level) ist der Standardzustand, der die erforderliche Anzahl von Bitfehlern erfasst. Wenn ein falscher Übergang erkannt wird, bleibt der FSM bis zum Zurücksetzen im Fehlerzustand. Die kritischen Ausgänge werden in den Zustand »sicher/inaktiv« versetzt.
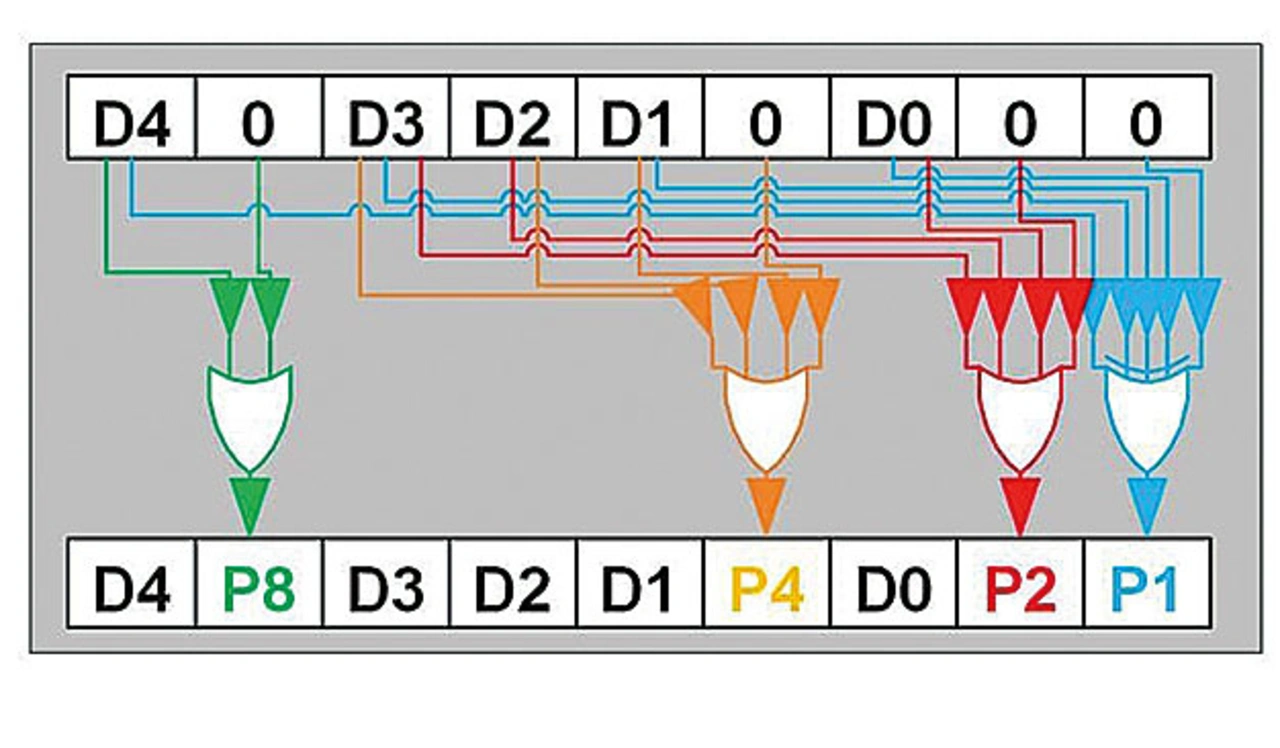
Das folgende Schema wird mit der SV-Funktion implementiert und liefert Hamming-Codes mit 3-Bit-Abstand für FSM-Zustände von bis zu 32, wobei Dx das jeweilige Bit der binär codierten Zustandsnummer ist und Px für die resultierende Paritätsprüfsumme steht (Bild 1, Bild 2):
➔ Code word = {D4, 0, D3, D2, D1, 0, D0, 0, 0}
➔ Resulting code (state) = {D4, P8, D3, D2, D1, P4, D0, P2, P1}
Die vorgeschlagene Technik schreibt kein bestimmtes FSM-Codierungsverfahren vor, wenn die Aufzählungszustandswerte den erforderlichen Mindest-HD zwischen zwei Zuständen aufweisen und der Fehlerzustand der Standardzustand ist, bei dem das Fehlerflag aktiviert ist.
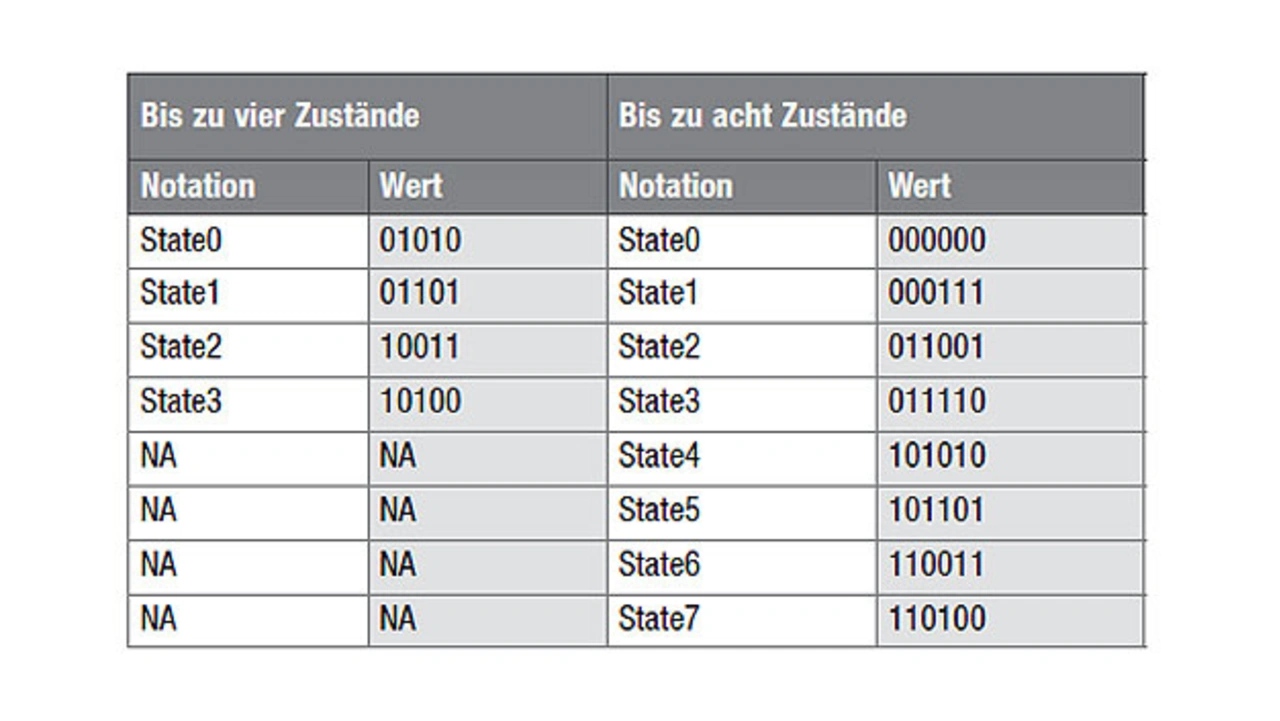
Sie kann mit den meisten der hier vorgeschlagenen Codierungsverfahren und Implementierungen genutzt werden [7]. Es wird empfohlen, entweder alle FSM-Ausgänge zu registrieren oder sicherzustellen, dass die FSM-Ausgänge ausschließlich vom aktuellen Zustand abhängen (Tabelle 1).
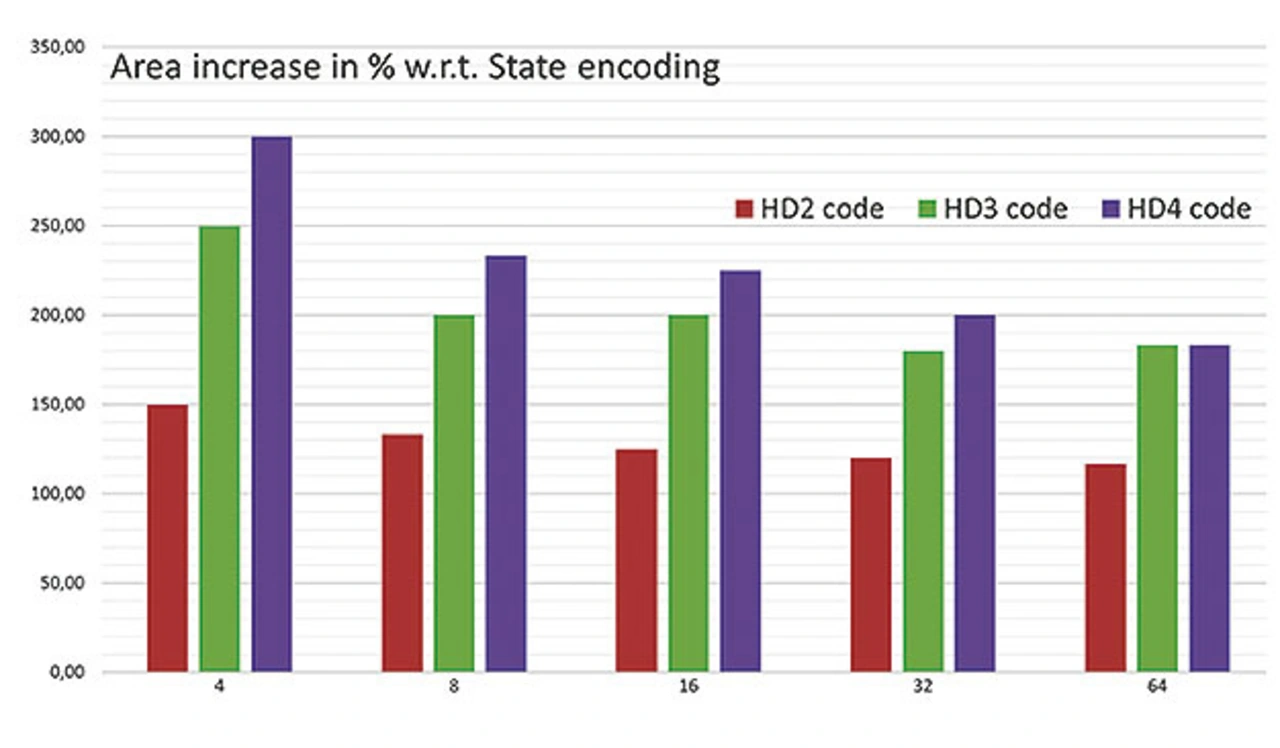
Bild 3 zeigt die Ergebnisse der Flächennutzung für verschiedene HD-Codes und die Anzahl der FSM-Zustände. In einigen Fällen erreicht der Flächenbedarf 300 % im Vergleich zu einer typischen binären Zustandscodierung für dieselbe Anzahl von Zuständen
Allgemeine sequenzielle logische Fehlererkennung
Alle Funktionsregister (FSM-Ausgangsregister, speicherzugeordnete Register, Zähler usw.) sollten in der Lage sein, eine Reihe von Fehlern basierend auf den FuSa-Anforderungen zu erkennen, das heißt Einzelbit-Fehlererkennungsfunktionen (mittels Paritätsprüfsumme) und Mehrbit-Fehlererkennungsfunktionen (mittels Cyclic Redundancy Check (CRC) oder ECC-Prüfsumme). Der vorgeschlagene Mechanismus ermöglicht eine kontinuierliche Überwachung der Prüfsummenbits für den nächsten Wert (kombinatorisch) und den aktuellen Wert (sequenziell).
Die Fehler können in der Logik des nächsten Zustands auftreten und werden nicht erkannt, was zu erwarten ist, da sie für die gesamte nachgelagerte Logik zum Einsatz kommen. Aufgrund der vorübergehenden Natur der Bit-Flip-Fehler und der Tatsache, dass Signale elektronisch und logisch verschlüsselt sind, kann der tatsächliche Effekt abgeschwächt werden, sodass er für die FuSa-Metriken akzeptabel ist. Bild 4 zeigt ein generalisiertes Diagramm.
Gemeinsame kombinatorische logische Fehlererkennung
Abhängig von der Vielfalt der kombinatorischen Funktionen können verschiedene Schemata genutzt werden, um Fehler zu erkennen. Folgende Hauptgruppen sind zu unterscheiden:
➔ Addierer/Subtrahierer und jede Art von allgemeiner Arithmetik
➔ Komparatoren
➔ Multiplexer/Encoder/Decoder
Der folgende Ansatz wird vorgeschlagen. Multiplexer werden vor der kombinatorischen Logik platziert, die überprüft werden soll. Bestimmte Testvektoren werden durchlaufen und das Ergebnis wird mit dem Erwartungswert verglichen. Abhängig von den implementierten Funktionen und dem gewählten Testvektor kann die angestrebte diagnostische Abdeckung erreicht werden. In einigen Fällen muss mehr als ein Testvektor angewendet werden, um die erforderliche Abdeckung zu erzielen.
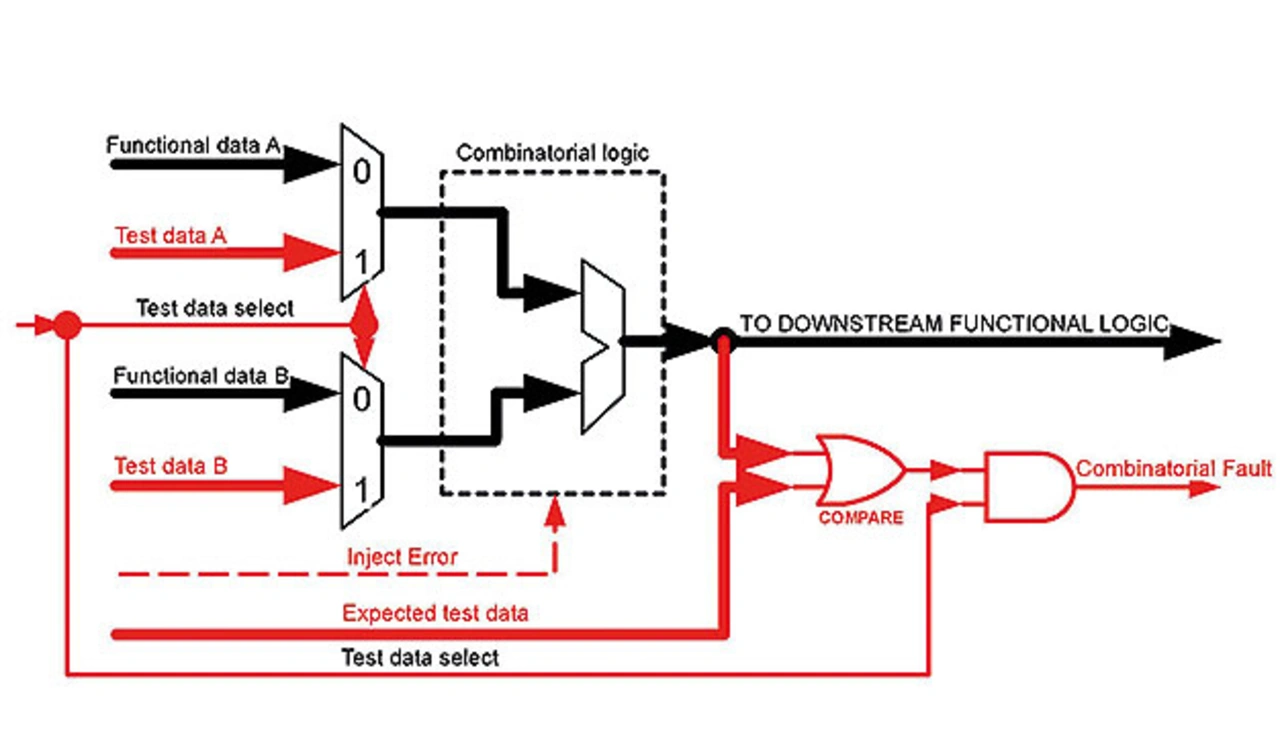
Diese Technik lässt sich auf eine kombinatorische Logik anwenden, die nicht kontinuierlich genutzt wird, das heißt nicht bei jedem Taktzyklus verwendet wird. Angesichts der Tatsache, dass dieses SM periodisch ausgeführt wird, muss das Zeitintervall für die Fehlererkennung (FDTI) [5] für das System berücksichtigt werden (Bild 5).
Erkennung latenter Fehler
Eine weitere Kategorie, die bei FuSa-bezogenen Produkten je nach ASIL-Qualität (typischerweise ASIL-C und D) berücksichtigt werden muss, sind die latenten Fehler. Einer der Hauptfaktoren sind die Fehler, die in der Fehlererkennungslogik selbst auftreten.
In der Regel besteht die Methode zur Behandlung dieser Fehler darin, die SMs regelmäßig oder kontinuierlich beim Einschalten zu testen. Dafür kann eine einfache Schnittstelle implementiert werden, die einen Fehler in den Prüfsummenbe-rechnungsalgorithmus einspeist. Die Ergebnisse werden an den Ausgängen der jeweiligen Logik überprüft. In allen nachfolgenden RTL-Beispielen wird die Fehlererkennung latenter Fehler bereitgestellt und unterstützt.
- Digitale Sicherheitsmechanismen in kritischen Systemen
- Implementierung in RTL
- Ergebnisse der Methodik
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Alle Beiträge im Überblick
Online-Themenwoche »Autonomes Fahren«
Algorithmen am Steuer
Die Risikobewertung autonomer Fahrzeuge
Renesas Electronics
Demos zeigen die Leistungsfähigkeit von Cortex-M85
Autonome Fahrtechnologien erproben
ZF eröffnet 5G-Netz auf Nutzfahrzeug-Teststrecke
Der Sinn eines Automotive OS
Auf dem Weg zum Software-definierten Fahrzeug
Der Weg zum autonomem Fahren
Ein Konnektivitätsstandard erobert die Automobilindustrie
Perfekte Umfelderkennung
LiDAR-Sensoren nahtlos integrieren
Fahrerassistenz und Sicherheit
Die Konnektivitäts-Anforderungen lösen – ein Überblick
