Schaltwandler in Computernetzteilen
MOSFETs nach neuer Leistungskennzahl auswählen
Fortsetzung des Artikels von Teil 1
MOSFETs steueren die Ausgangsspannung bei Dauerstrombetrieb
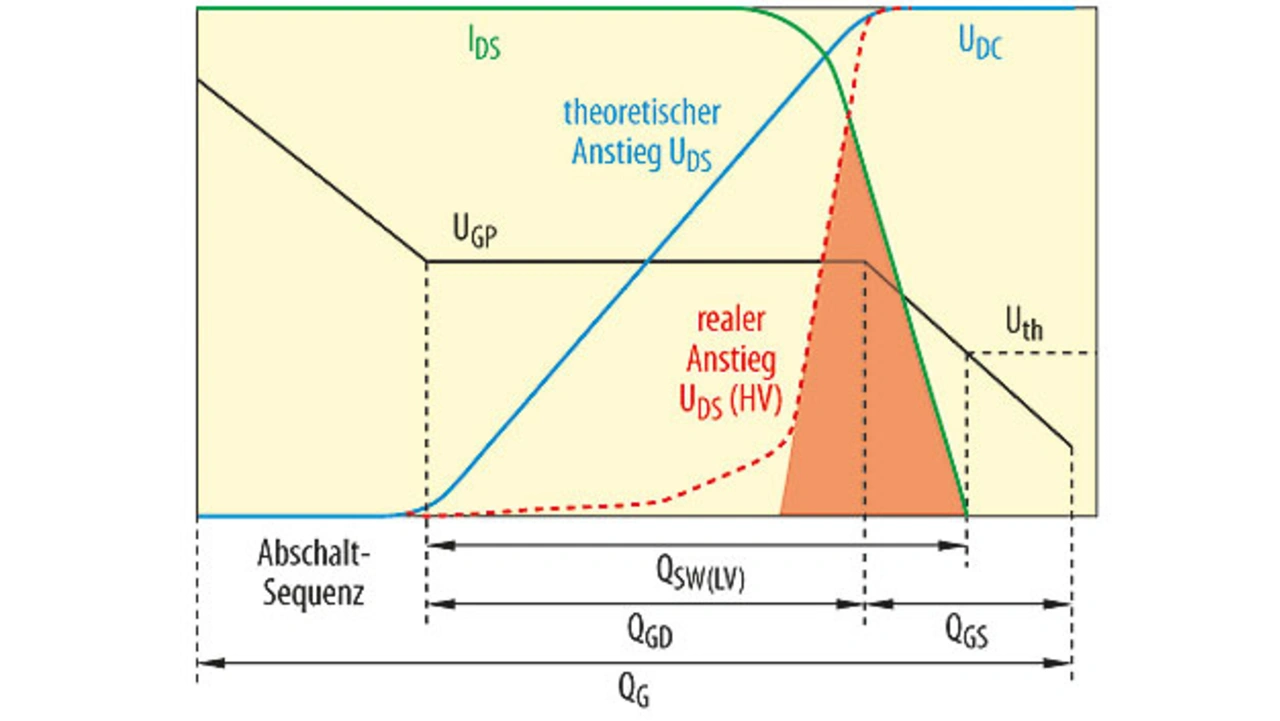
Bild 3 zeigt das Standard-Gate-Ladungsmodell für den Abschaltvorgang. Im Dauerstrombetrieb schaltet der MOSFET gegen die Ausgangsspannung UDC ständig ein und aus. Die Schaltverluste sind eine Funktion von UDC, IAC und den Schaltzeiten TSWon und TSWoff. Wie in [1] erläutert, überspannt der theoretische Anstieg der Drain-Spannung (blau gezeichnet) das komplette Miller-Plateau, das von QQD dargestellt wird. QSW ist die effektive Schaltladung, eine Kombination von QGS und QGD. Bei einem effektiven Konstantstrom von IGon und IGoff gilt:
und
wobei
MOSFET-Datenblätter führen typischerweise QGS und QGD auf, aber nicht in jedem Fall QSW, die effektive Schaltladung. Für Niederspannungs-MOSFETs lässt sich QSW näherungsweise nach der folgenden Gleichung berechnen:
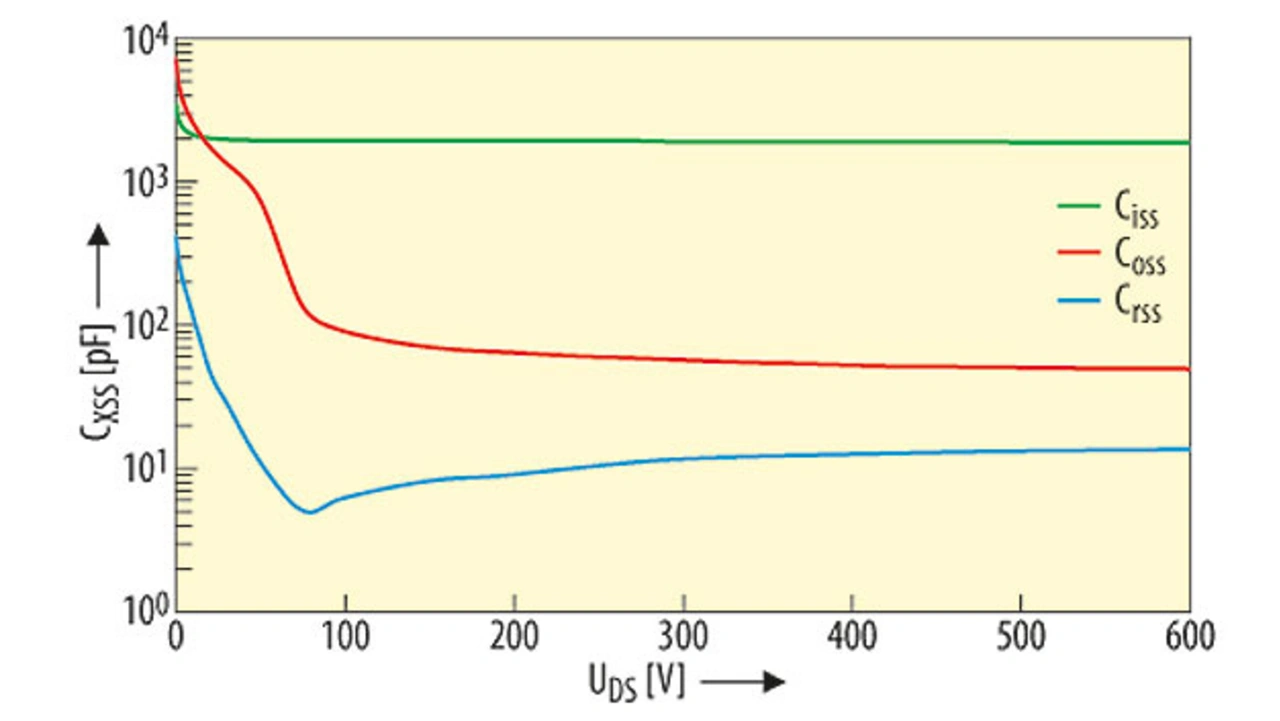
Für Hochspannungs-MOSFETs funktioniert diese Approximation aber nicht, weil deren Parasitärkapazitäten zu stark variieren. Bild 4 zeigt eine typische Variationsbreite dieser Kapazitäten für Hochspannungs-Superjunction-MOSFETs. Innerhalb der ersten 100 V können CRSS und COSS um einen Faktor 100 variieren.
In Bild 3 basiert der blau dargestellte theoretische Anstieg von UDS auf dem Gate-Ladungsmodell eines Niederspannungs-MOSFET. In Wirklichkeit sieht der Anstieg von UDS eher aus wie die gestrichelte rote Linie. Der zugehörige Schaltverlust (roter Bereich) ist also deutlich kleiner als angenommen – wenn man das komplette Miller-Plateau berücksichtigt. Um eine Übereinstimmung zu den tatsächlich beobachteten Anstiegs- und Abfallzeiten zu erzielen, kann man für QSW folgendermaßen schreiben:
Die Gleichung ist empirisch; sie wurde aufgestellt, damit sie zu den beobachteten Schaltzeiten von Hochspannungs-MOSFETs passt, speziell zu Superjunction-Typen. Sie stimmt recht gut mit den Typen der Familie E überein. Manche Autoren arbeiten im Interesse besserer Ergebnisse in der konventionellen Formel für die Kennzahl mit QGD statt mit QD. Wie gezeigt, hängt keine der beiden Zahlen direkt mit TSW zusammen, der echten Maßzahl für den Schaltverlust.
Mit dieser guten Schätzung für den Durchlassverlust beträgt der Gesamtverlust:
In einer hart geschalteten Schaltung wie einem CCM-Schaltnetzteil wird die Ausgangskapazität des MOSFET in jedem Zyklus zweimal geladen und entladen, wobei die gespeicherte Energie EOSS jeweils verlorengeht. Die Verluste betragen also:
Wiederum braucht man aufgrund der nichtlinearen Charakteristik eine andere Berechnung für die Energie, die bei hoher Spannung in Coss gespeichert ist. Die herkömmliche Formel zur Berechnung der in einem Kondensator gespeicherten Energie (nämlich ½ CU²) funktioniert hier nicht. Zur Berechnung der in einem MOSFET gespeicherten Energie geben die Hersteller einen weiteren Parameter namens COER an. Der Parameter ist üblicherweise für 400 V oder 480 V spezifiziert und ist der Kapazitätswert eines Festkondensators, der bei den genannten Spannungen die gleiche Energie speichern kann wie das Coss eines MOSFET. In neuerer Zeit geben die Hersteller sogar die vollständige Eoss-Kurve in den Datenblättern an.
In Schaltreglern spielen die Verluste der Bodydiode keine Rolle; daher können die Parameter UFWD und QRR mit den zugehörigen Verlusten vernachlässigt werden. Die übliche Schaltfrequenz in Schaltreglern im Dauerstrombetrieb liegt mit 65 kHz bis 70 kHz verhältnismäßig niedrig. Diese niedrige Frequenz legt zusammen mit einem niedrigen QG nahe, dass Verluste durch die Ansteuerung des Gate keine große Rolle spielen, somit auch vernachlässigt werden können. Die Gesamtverluste ergeben sich aus der Addition:
Diese Gleichung mag recht kompliziert und sperrig erscheinen, aber ein zweiter Blick zeigt, dass die meisten anwendungsbezogenen Werte bereits bekannt sind. Wir ersetzen daher die folgenden, üblicherweise in Schaltreglern verwendeten Werte:
- UEin = 100 V (AC) minimal
- UDC = 400 V
- FSW = 70 kHz
- TCR = 2 für 600-V-MOSFETs.
Die Verlustgleichung vereinfacht sich somit zu
wobei PEin in kW angegeben ist, RDS(on) in mΩ und QSW in nC.
Es muss an dieser Stelle nochmals wiederholt werden, dass der Zweck dieser Gleichung keine hochpräzise Berechnung der Verluste ist. Sie dient vielmehr als Werkzeug zum Vergleich verschiedener MOSFET-Typen. Für jeden vorgegebenen Wert PEin und den zugehörigen Gatestrom IGEQ kann man aus dem Datenblatt des MOSFET die entsprechenden Werte von RDS(on), QSW und COER herauslesen und dann die Verluste vergleichen. Verwendet man PTOTAL als verlustbasierte Kennzahl, basiert die Bauteilauswahl nun auf den erwarteten Verlusten bei realistischen Betriebsbedingungen statt lediglich auf dem Produkt RDS(on) · QG, das allenfalls einen Anhalt gibt. Um dies weiter zu illustrieren, betrachten wir einen Referenz-MOSFET mit 600 V Sperrspannung und den folgenden weiteren Werten:
RDS(on) = 100 mΩ
Qsw = 16 nC
COER = 120 pF bei 400 V.
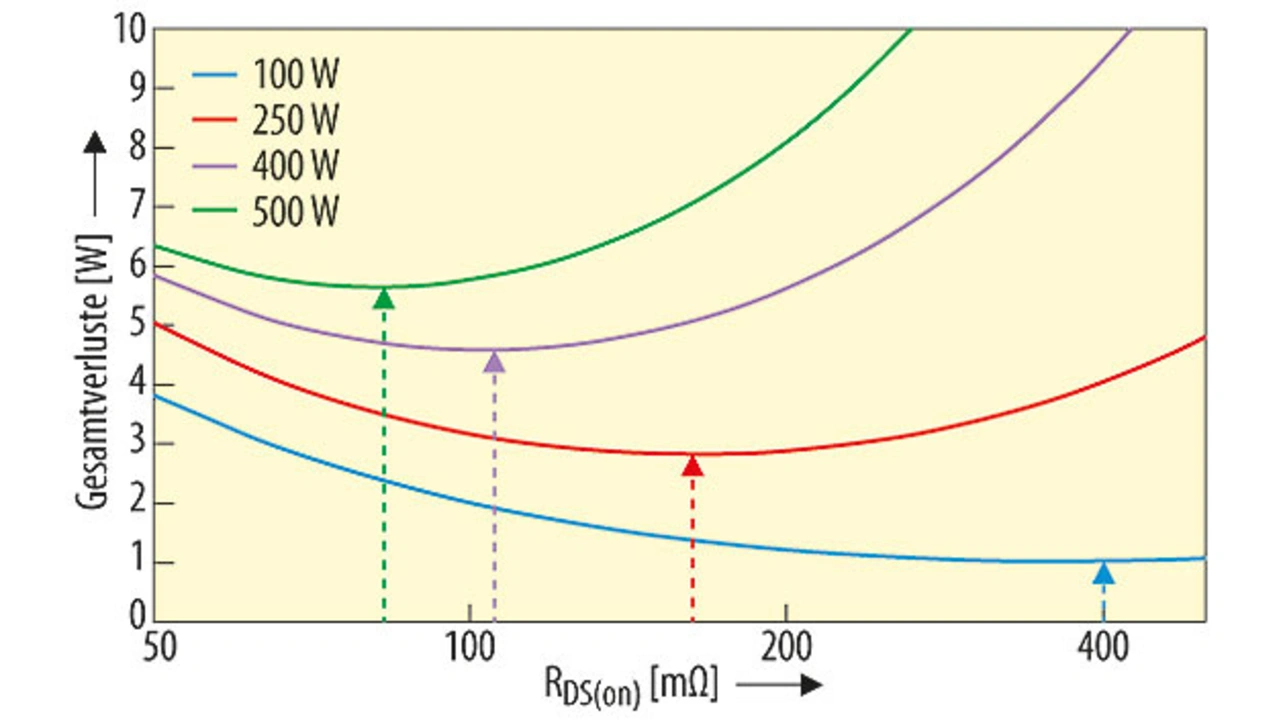
Wenn wir das gleiche Produkt RDS(on) · QG annehmen und alle Kapazitätswerte umgekehrt proportional zu RDS(on) skalieren, können wir eine hypothetische Familie von MOSFETs definieren, deren RDS(on)-Werte zwischen 50 und 500 mΩ variieren. Bei unterschiedlichen Eingangsleistungen ergibt die Verlustgleichung dann die Kurvenschar in Bild 5, aus der sich unmittelbar zwei Erkenntnisse ergeben:
- Erstens: „Niedrigster RDS(on)“ führt nicht unter jeder Betriebsbedingung zum geringsten Verlust. Bei jeder Leistung gibt es einen optimalen Wert von RDS(on), bei dem der Wirkungsgrad maximal ist. Verringert man RDS(on) demgegenüber weiter, wird das nicht nur teurer, sondern der Verlust wird sogar wieder größer. Bei 250 W Ausgangsleistung zeigt ein 400-mΩ-MOSFET die gleiche Performance wie ein 70-mΩ-MOSFET, und doch sind beide nicht die beste Lösung für diese Ausgangsleistung. Der optimale RDS(on) für diese Ausgangsleistung liegt zwischen 160 und 170 mΩ.
- Zweitens ist das Produkt RDS(on) × QG ein schlechter Ratgeber bezüglich der Performance. Alle Typen, die im Graphen verglichen wurden, weisen den gleichen Wert für RDS(on) x QG auf, zeigen aber abhängig von den Betriebsbedingungen eine unterschiedliche Leistung.
- MOSFETs nach neuer Leistungskennzahl auswählen
- MOSFETs steueren die Ausgangsspannung bei Dauerstrombetrieb
- Nutzen der neuen Kennzahl
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
GaN-Transistoren in Stromversorgungen
Neue Stufe der Leistungsfähigkeit
Designpraxis
DC/DC-Wandler als Gate-Treiber
Vier Konstantstrom-Kanäle
DMOSFET-Arrays mit 1,5-A-Senkenausgangstreiber
