Startseite > Medizintechnik > E-Health > Neuronale Netze statt Nadel und Spritze

Mit KI nichtinvasiv Blutzucker bestimmen

Neuronale Netze statt Nadel und Spritze

11. April 2017, 10:00 Uhr | Hartmut Fischer

▶ Diesen Artikel anhören

Fortsetzung des Artikels von Teil 2

Prinzip der Blutzuckermessung

Das von Trout entwickelte Messgerät macht sich den Zusammenhang zwischen Blutzuckergehalt und Impedanz des Blutes im menschlichen Organismus zunutze. Steigt der Glukosespiegel, nimmt auch der osmotische Druck zu. Die Zellen werden kleiner, das extrazelluläre Flüssigkeitsvolumen Vout steigt. Daraus resultiert ein größerer Abstand zwischen den Zellen. Die Folge: Die Leitfähigkeit C steigt und die Impedanz Z nimmt ab.
Mithilfe eines in den Körper geleiteten hochfrequenten Stroms lässt sich die Impedanz in der Gesamtflüssigkeitsmenge ermitteln.
Diese ergibt sich zu Vtot = Vin + Vout.
(Vin = Flüssigkeitsvolumen in der Zelle; Vout = Flüssigkeitsvolumen außerhalb der Zelle). Ein niederfrequenter Strom eignet sich hingegen nur für das Ermitteln der Impedanz im Flüssigkeitsvolumen außerhalb der Zellen. Insgesamt ergibt sich für den Zusammenhang zwischen Impedanz Z und dem Flüssigkeitsvolumen im Gewebe folgende Abhängigkeit:

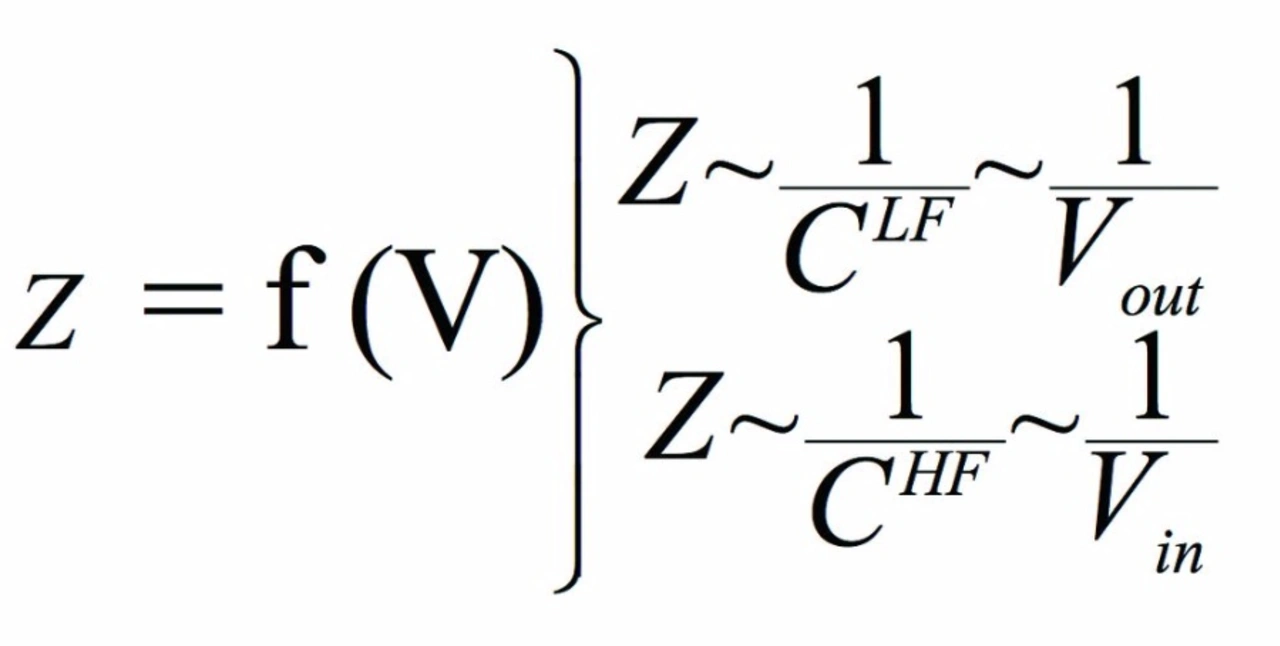
Für den niederfrequenten Anteil verhält sich der Impedanzwert also umgekehrt proportional zur niederfrequenten Leitfähigkeit und damit umgekehrt proportional zum außerzellulären Flüssigkeitsvolumen Vout. Im Fall des hochfrequenten Anteils verhält sich der Impedanzwert ebenfalls umgekehrt proportional zur hochfrequenten Leitfähigkeit C und damit umgekehrt proportional zur Summe Vtot aus interzellulärem Flüssigkeitsvolumen Vin und außerzellulärem Flüssigkeitsvolumen Vout.
Bei der Korrelation zwischen Blutzucker und Impedanz gibt es allerdings ein Problem: Der Zusammenhang ist nichtlinear; Faktoren wie subjektive Parameter und Umgebungsbedingungen wirken sich darauf aus. Daher ist es nicht möglich, ihn mit einem festen Algorithmus zu beschreiben.
Eine probate Lösung ist die Verwendung eines kalibrierten KNN. Vorteil des lernfähigen Netzes: Je öfter das Verfahren Kalibriervorgänge und Messungen vornimmt, desto genauer wird es. Im Laufe der Zeit stellt es sich immer besser auf den jeweiligen Patienten ein. Weiterhin ist das Blutzuckermesssystem als ein relatives Messsystem ausgelegt. Das heißt, es ist keine Kalibrierung gegen ein Normal notwendig und Störungen eliminieren sich durch die Nutzung zweier Elektroden.
Eine weitere Schwierigkeit: Ein Anstieg der Glukosekonzentration führt zu einer höheren Leitfähigkeit des Gewebes, jedoch kann sich die Leitfähigkeit der Elektroden durch die Trockenheit der Haut verringern – der elektrische Widerstand nimmt zu. Dies würde das Messergebnis verfälschen. Daher haben die Trout-Ingenieure eine Messmethode entwickelt, die den Feuchtegrad der Haut einbezieht: mit einem zweiten Elektrodenpaar, über das sich der feuchtebedingte Kontakteinfluss kompensieren lässt. Zusätzlich wurde durch eine Messung mit zwei Messfrequenzen sowie deren spezielle Frequenz und Kurvenform eine signifikante Verbesserung der Ergebnisse erreicht.
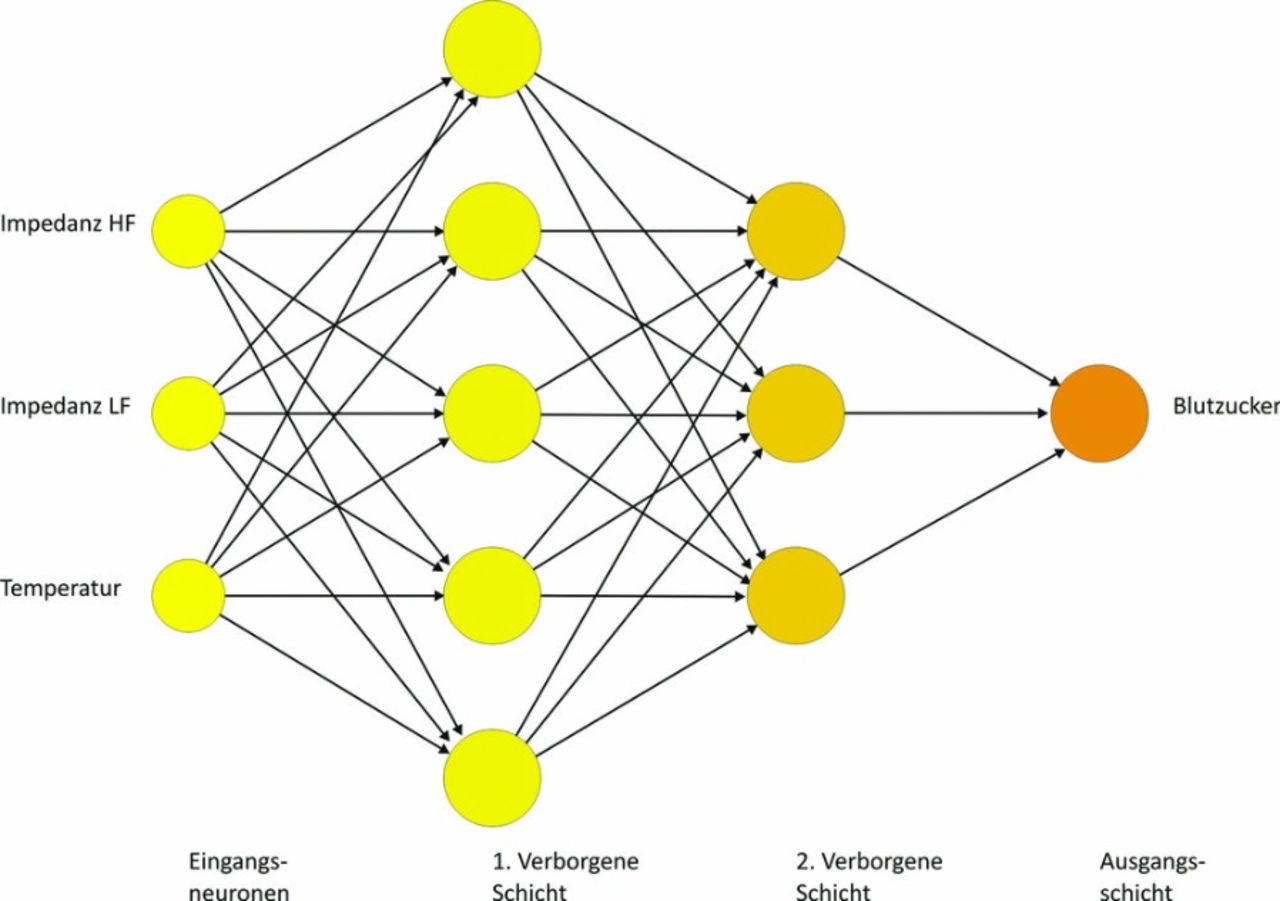
Ein KNN besteht aus Neuronen, die in Schichten angeordnet und durch Synapsen untereinander verbunden sind. Jedes neuronale Netz besitzt eine bestimmte Anzahl von Eingangsneuronen sowie eine Ausgangsschicht, die die Ausgangsneuronen enthält. Weiterhin besitzt ein KNN üblicherweise mindestens eine verborgene Schicht, die die verborgenen Neuronen enthält. Das von Trout entwickelte KNN besteht aus drei Schichten.
Über die Eingangsneuronen werden die vorhandenen Daten aufgenommen und in das neuronale Netz eingespeist. Die Daten durchlaufen die Neuronen aller Schichten und werden dabei bearbeitet. Über die Ausgangsneuronen werden schließlich die berechneten Ergebnisse ausgegeben. Im Einzelnen erfolgt die Transformation der Daten bei der Weitergabe an die verschiedenen Schichten des neuronalen Netzes so, dass ein Neuron entweder die Eingabedaten oder bearbeitete Daten von Neuronen der vorhergehenden Schicht empfängt. Die Daten werden gewichtet und anschließend addiert. Von der Summe wird ein Schwellenwert abgezogen und aus dem daraus resultierenden Ergebnis wird mit Hilfe der Transferfunktion der Wert berechnet, den das Neuron weitergibt. Dabei kommt die Tan-Sigmoid- Funktion der Transferfunktion in den Neuronen der verborgenen Schichten zum Einsatz:
T(n)=1/(1+e^(–2n) )–1
In den Eingangsneuronen sowie in den Neuronen der Ausgangsschicht wird als Identitätsfunktion ebenfalls T(n) genutzt.
Bei den genutzten KNN sind zwei verborgene Schichten und eine Ausgangsschicht vorhanden, wobei die erste verborgene Schicht fünf Neuronen enthält, und die zweite dahinter angeordnete verborgene Schicht drei Neuronen und die Ausgangsschicht ein Neuron. Grundsätzlich ist die Anzahl der Neuronen in einem neuronalen Netz allerdings nicht beschränkt.
Für die Genauigkeit der Ergebnisse, insbesondere des Blutzuckergehalts, ist die Wertebelegung der Gewichte und der Schwellenwerte entscheidend. Die Schwellenwerte und Gewichte innerhalb des neuronalen Netzes werden zunächst mit zufällig gewählten beliebigen Werten belegt. Zum Training werden dann dem Netz Daten, also Impedanzen und Temperaturwerte und die dazugehörigen Ergebnisse (Blutzuckergehalt) präsentiert. Das Netz berechnet aus den gegebenen Daten einen Wert, der mit dem bekannten Wert, hier dem invasiv gemessenen Blutzuckerwert, verglichen wird. Aufgrund der Abweichungen werden die Schwellenwerte und Gewichte im Netz korrigiert. Dies geschieht durch numerische Verfahren, etwa durch den Levenberg-Marquardt-Algorithmus. Dieser Vorgang des Lernens wird für ein neuronales Netz so lange wiederholt, bis die Abweichung einen gewünschten Wert nicht überschreitet.