Passives Bus-Biasing
Ausfallsichere RS-485-Netze
Fortsetzung des Artikels von Teil 1
Zweifach ausfallsicheres Biasing-Konzept
Um VAB über lange Kabelstrecken konstant zu halten, ist an beiden Busenden ein ausfallsicheres Biasing erforderlich (Bild 3). Jedes Biasing-Netzwerk kompensiert den Biasing-Verlust des anderen Netzwerks entlang des Kabelverlaufs. Die Anforderungen an die Abschlusswiderstände RT sind die gleichen wie für RT2 im einfach ausfallsicheren Biasing-Netzwerk, wobei Z0 = 2·RB || RT entsprechen muss. RT muss daher für einen gegebenen Wert von RB folgende Gleichung erfüllen:
Die Bedingung für die Gleichtaktbelastung ändert sich jedoch, da an jedem Leiter jetzt zwei Biasing-Widerstände parallelgeschaltet zur Masse anliegen. Daher muss die Parallelschaltung aus RB/2 und REQ größer oder gleich RCM sein. Für einen gegebenen Wert von RB beschränkt sich REQ somit auf:
Jobangebote+ passend zum Thema
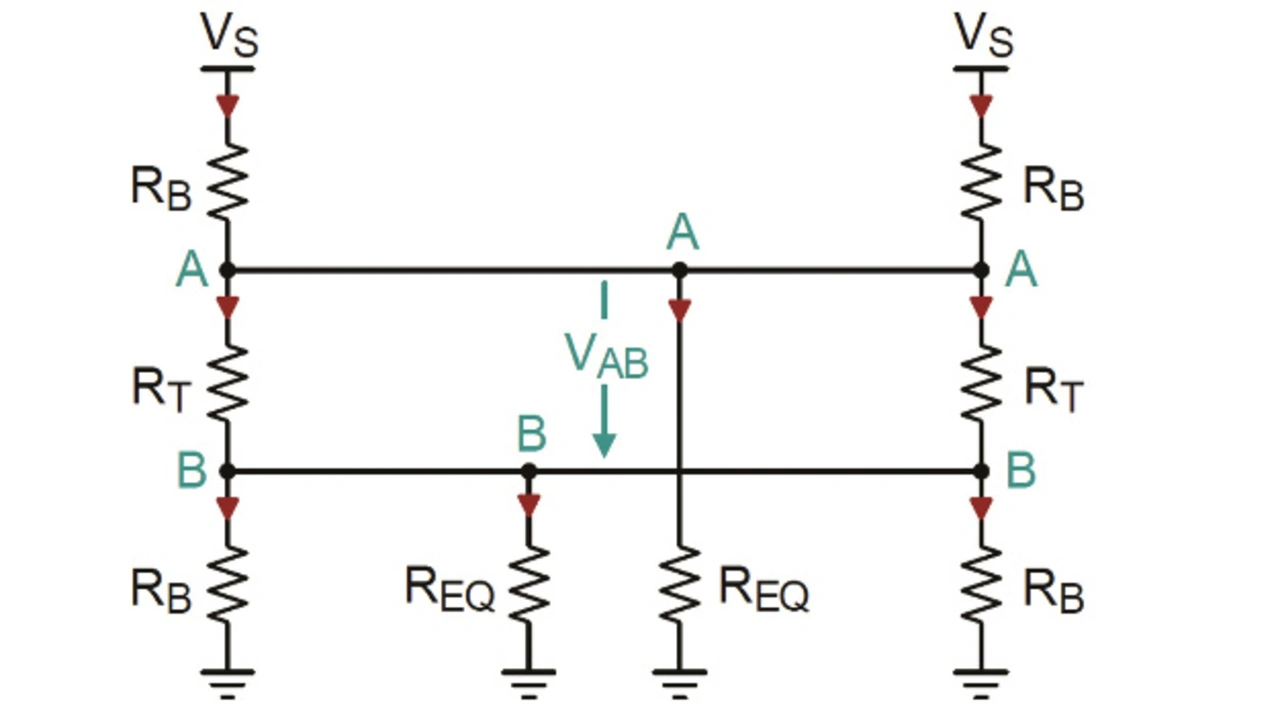
Um die Gleichung für RB aufzustellen, sind die Knotenströme in A und B zu bestimmen. Da die Biasing-Netze identisch sind, treiben sie die gleiche Strommenge durch REQ. Um daher VAB in der Mitte des Busses zu bestimmen, ist nur ein Stromwert durch REQ zu ermitteln und um den Faktor 2 zu multiplizieren:
Die Berechnung der Knotenströme für die einzelnen Leitungsspannungen VA und VB sowie die Berechnung der Differenz zwischen beiden Werten ergibt die differenzielle Busspannung VAB:
Setzt man die Gleichungen (10) und (11) in Gleichung (14) ein, so ergibt sich die endgültige Gleichung für VAB:
Löst man die Gleichung nach RB auf, so ergibt sich der erforderliche Mindestwert für den Bias-Widerstand folgendermaßen:
Mit RB lässt sich nun die maximale Anzahl an Transceiver-Einheitslasten folgendermaßen berechnen:
Rechenbeispiele
In den folgenden Beispielen wollen wir die Widerstandswerte für ein- und zweifach ausfallsichere Biasing-Netzwerke einer kurzen und einer langen Datenstrecke unter der Annahme eines Wellenwiderstands Z0 von 120 Ω berechnen. In diesem Beispiel kommt ein Bus-Transceiver ISL8487E von Renesas Electronics zum Einsatz. Dieser Baustein ist ein 1/8-UL-Transceiver mit einer minimalen Versorgungsspannung VS von 4,75 V. Der maximale Eingangsschwellenwert des Empfängers beträgt 200 mV, was bei einem angenommenen Rauschabstand von 100 mV eine Leerlauf-Busspannung VAB von 300 mV erfordert.
- Für ein einfach ausfallsicheres Netzwerk
Es sei RT1 = Z0 = 120 Ω. Daraus lässt sich anhand Gleichung (8) der Wert von RB berechnen; dieser liegt bei 467,6 Ω. Dementsprechend wählt man aus der E-96-Reihe den Standardwert 470 Ω. Als nächstes errechnet man RT2 anhand Gleichung (2) zu 137,6 Ω. Dies entspricht dem Standardwert 138 Ω aus der E-96-Reihe. Abschließend lässt sich nUL anhand Gleichung (9) bestimmen; dieser Wert liegt bei 6,4 UL. Folglich beträgt die maximale Anzahl der 1/8-UL-Transceiver (6,4 UL)/(1/8 UL) = 51.
- Für ein zweifach ausfallsicheres Netzwerk
Der Wert von RB lässt sich anhand von Gleichung (16) ermitteln; dieser liegt bei 935,2 Ω. Dementsprechend wählt man aus der E-96-Reihe den Standardwert 942 Ω. Als nächstes errechnet man RT2 anhand Gleichung 2 zu 128,2 Ω. Dies entspricht dem Standardwert 129 Ω aus der E-96-Reihe. Abschließend lässt sich nUL anhand Gleichung 1 bestimmen; dieser Wert liegt bei 6,5 UL. Folglich beträgt die maximale Anzahl der 1/8-UL-Transceiver (6,3 UL)/(1/8 UL) = 52.
Da der Wert von RB für zweifach ausfallsicheres Biasing doppelt so hoch ist wie der Wert von RB für einfaches Failsafe-Biasing, bleibt nUL für beide Anwendungen gleich.
- Ausfallsichere RS-485-Netze
- Zweifach ausfallsicheres Biasing-Konzept
- Auswahl des Transceivers
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Renesas Electronics
Automotive-MCU mit Virtualisierung
Isolierte RS-485-Transceiver
Isolation mit GMR-Technik
Security by Design
Sicher von Anfang an
Link Network Protocol auf RS-485-Basis
Serielles Gerätenetzwerk
Dual-Protokoll-Transceiver
Schnittstellen für Industrie-PCs vereinfachen
Für die Automatisierungstechnik
Einfache Multi-Protokoll-Kommunikation
Industrielle Kommunikation
Schnell mit RS-485
Power-Management/Analog
Renesas übernimmt Intersil für 3,2 Mrd. US-Dollar in bar
Intersil (2.Teil)
Ein Tutorial über RS-485-Transceiver
Intersil (1. Teil)
Ein Tutorial über RS-485-Transceiver
