Startseite > Power > Spannungswandler > Schaltregler mit doppelter Regelschleife schwingt nicht mehr

Stromversorgung für HF-Schaltkreise

Schaltregler mit doppelter Regelschleife schwingt nicht mehr

27. April 2020, 11:30 Uhr | Ricky Yang, Analog Devices

▶ Diesen Artikel anhören

Fortsetzung des Artikels von Teil 1

Hybride Rückkopplung

Bild 5 zeigt die neue hybride Rückkoppelstruktur. Die Idee dahinter ist es, die Regelschleife über eine zusätzliche Kondensatorrückkopplung vom ersten LC-Filter zu stabilisieren. Die äußere Spannungsrückkopplung vom Ausgang über einen Spannungsteiler wird nachfolgend als »externe Spannungsrückkopplung« bezeichnet, die innere Spannungsrückkopplung über den Kondensator C_F als »lokale Spannungsrückkopplung«. Beide Rückkopplungen – die externe wie die lokale – übertragen unterschiedliche Informationen aus der Frequenzdomäne.

Matchmaker+ Anbieter zum Thema

zu Matchmaker+

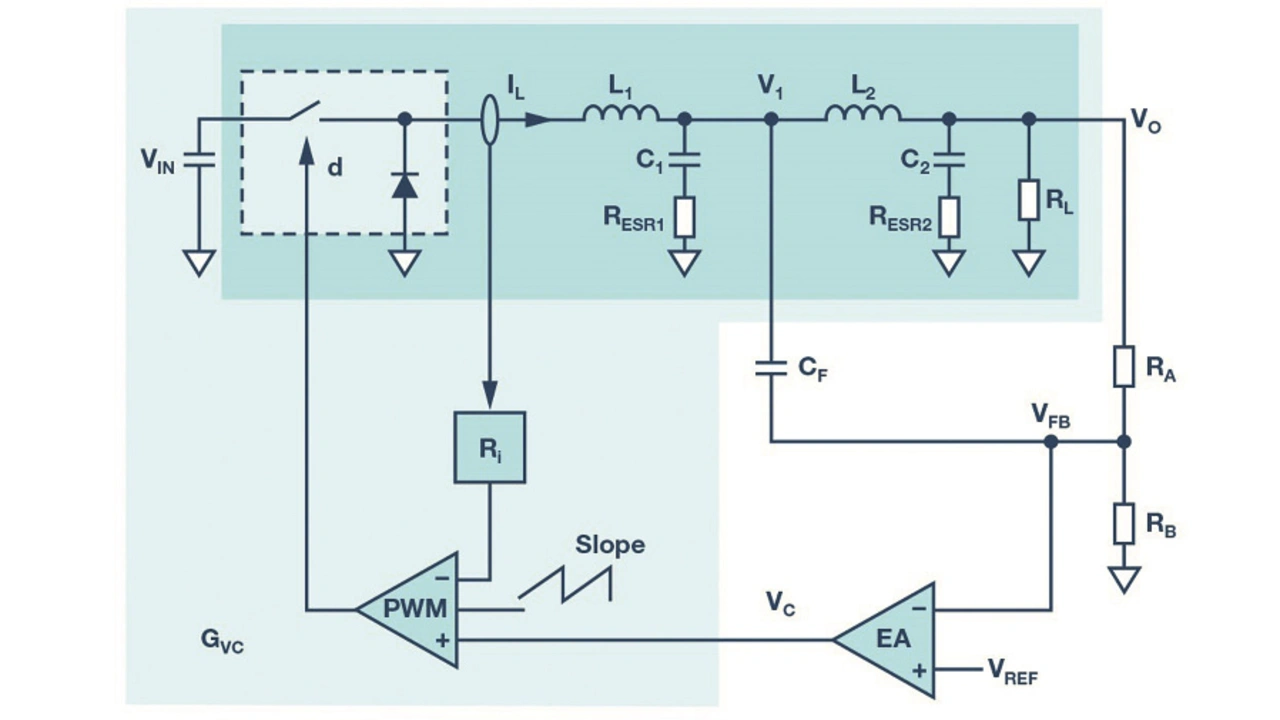
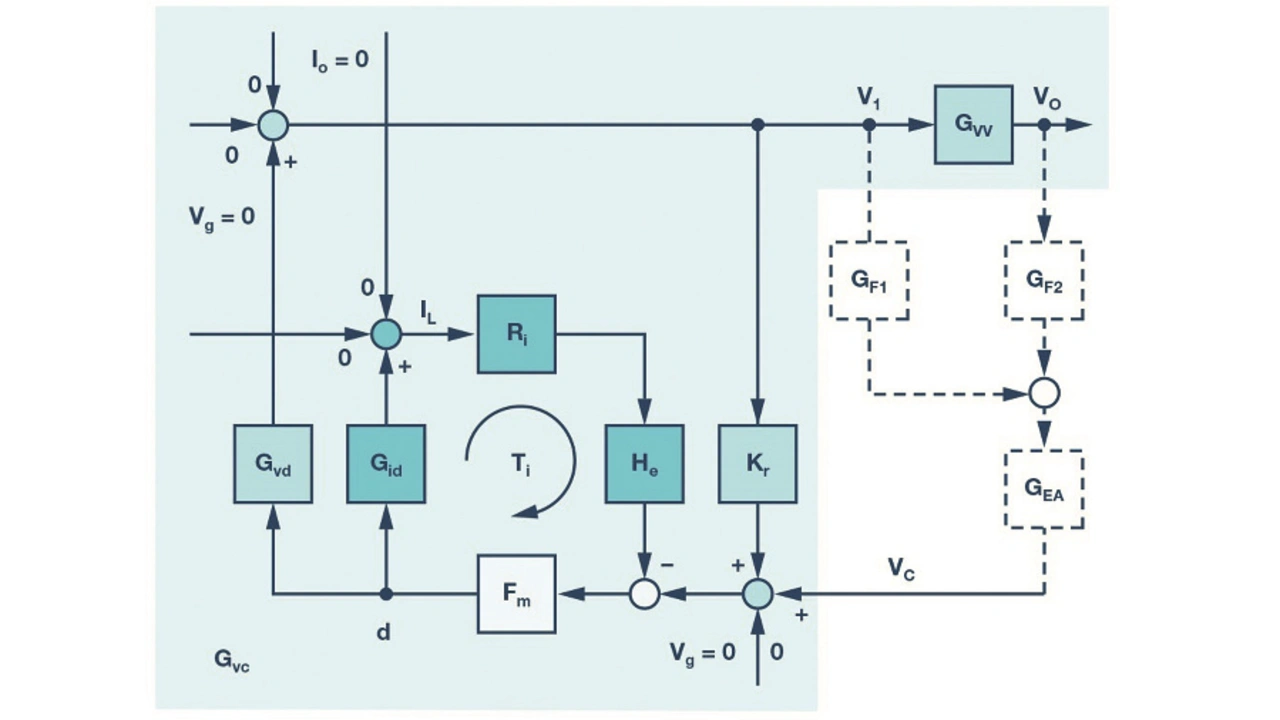
Die externe Rückkopplung liefert vor allem niederfrequente Signalanteile, um eine gute DC-Regelung des Ausgangs zu erreichen, während die lokale Rückkopplung die hochfrequenten Signalanteile liefert, um eine gute DC-Stabilität des Systems zu gewährleisten. Bild 6 zeigt das vereinfachte Kleinsignalblockdiagramm für die Schaltung aus Bild 5.

Die resultierende äquivalente Übertragungsfunktion der hybriden Rückkoppelstruktur unterscheidet sich deutlich von der Übertragungsfunktion der konventionellen Rückkopplung über Widerstandsteiler (genaue Herleitung findet sich in [7]):

$G subscript F B end subscript equals V subscript F B end subscript over V subscript 0 equals equals fraction numerator 1 plus open parentheses alpha plus R subscript E S R 2 end subscript times C subscript 2 close parentheses times S plus alpha times open parentheses begin display style L subscript 2 over R subscript L end style plus R subscript E S R 2 end subscript times C subscript 2 close parentheses times S squared plus alpha times L subscript 2 times C subscript 2 times S cubed over denominator open parentheses beta plus alpha times S close parentheses times open parentheses 1 plus R subscript E S R 2 end subscript times C subscript 2 times S close parentheses end fraction$

Diese Übertragungsfunktion besitzt mehr Nullstellen als Polstellen, und die zusätzlichen Nullstellen führen bei der Resonanzfrequenz, die von L₂ und C₂ bestimmt wird, zu einem vorlaufenden Phasenversatz von 180°. Deshalb kompensieren die zusätzlichen Nullstellen in der Übertragungsfunktion der Rückkopplung die zusätzliche Phasenverzögerung in der Übertragungsfunktion der Regelung der Ausgangsspannung. Dies vereinfacht das Design der Kompensation basierend auf der vollständigen Übertragungsfunktion von der Regelung bis zur Rückkopplung.

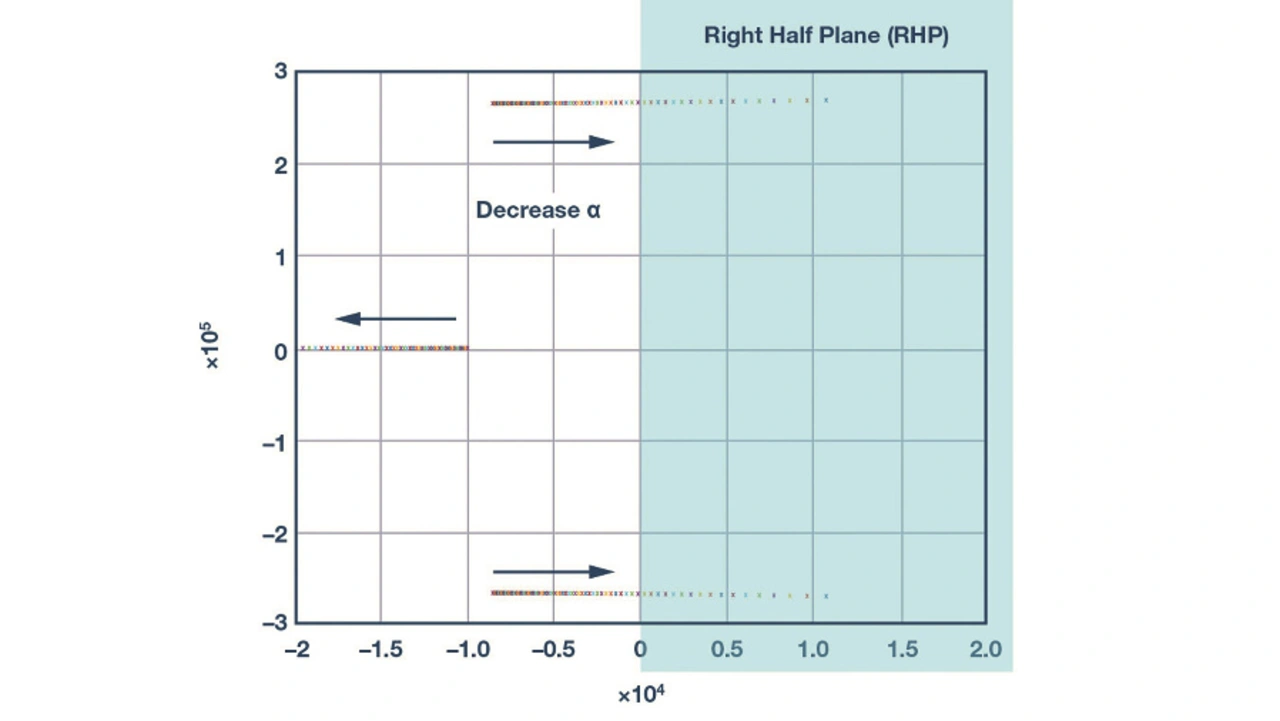
Abgesehen von den Parametern in der Leistungsstufe gibt es zwei weitere Parameter in der Übertragungsfunktion der Rückkopplung. Parameter β (= 1+ R_A/R_B) ist das Vergrößerungsverhältnis der Ausgangsspannung, das bereits gut bekannt ist. Der Parameter α (= R_A·C_F) ist in diesem Konzept jedoch völlig neu. Dieser Rückkoppelparameter lässt sich einstellen, um das Verhalten der Übertragungsfunktion der Rückkoppelung zu verstehen; die genaue Herleitung findet sich in [7]. Bild 7 zeigt die Änderung der Nullstellen in der Rückkoppelübertragung, wenn der Wert von α steigt. Es zeigt sich deutlich, dass bei erhöhtem α ein Paar von konjugierten Nullstellen von der linken in die rechte Halb-Ebene (RHP) wandert.

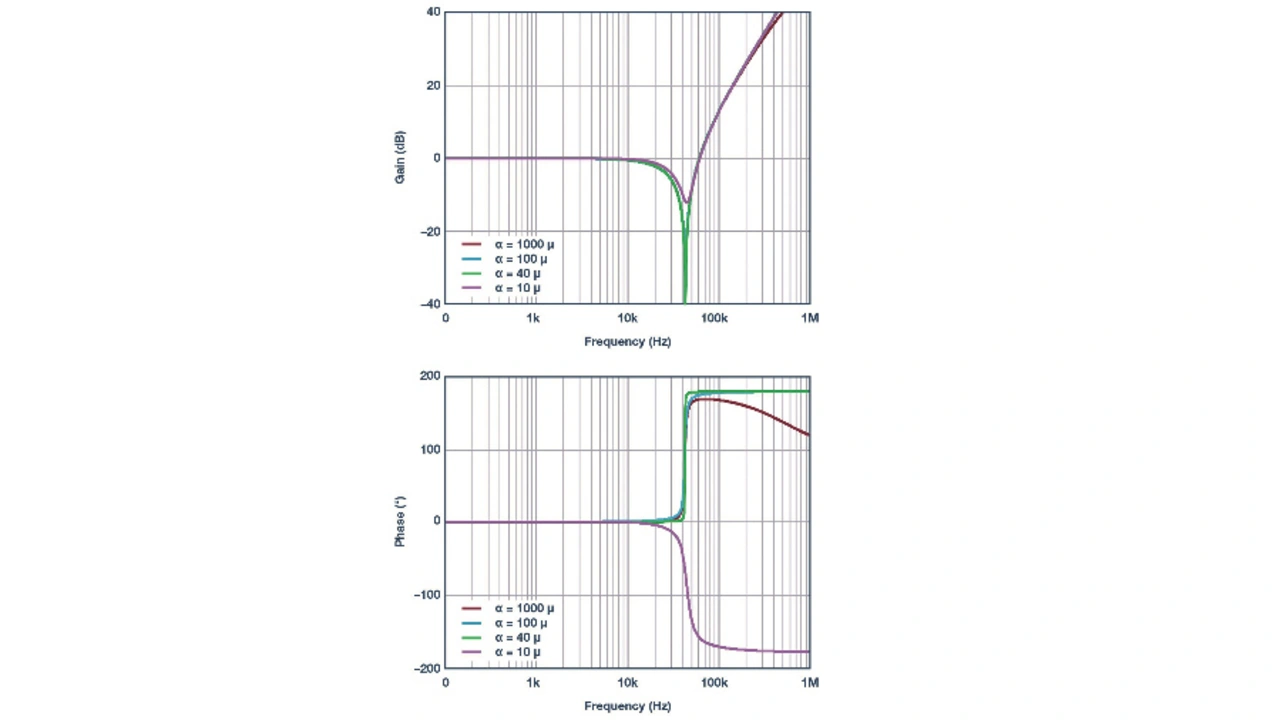
Bild 8 zeigt den Frequenzgang der Rückkoppel-Übertragungsfunktion bei unterschiedlichen Werten von α. Sinkt α auf den Wert 10^–6 (z. B. wenn R_A = 10 kΩ und C_F = 1 nF), weist die Übertragungsfunktion des Rückkoppelnetzwerks eine Phasenverzögerung von 180° auf. Dies bedeutet, dass die komplexen Nullstellen auf rechte Halb-Ebene gerutscht sind. Die Rückkoppel-Übertragungsfunktion lässt sich in einer neuen Form vereinfachen:

$G subscript F B _ a p p r end subscript equals fraction numerator 1 plus alpha times S over denominator open parentheses beta plus alpha times S close parentheses times open parentheses 1 plus R subscript E S R 2 end subscript times C subscript 2 times S close parentheses end fraction times increment$

Um die Nullstellen in der linken Halb-Ebene zu halten, sollte der Parameter α die folgende Bedingung erfüllen:

$space alpha greater than fraction numerator L subscript 2 times C subscript 2 over denominator begin display style L subscript 2 over R subscript L end style plus R subscript E S R 2 end subscript times C subscript 2 end fraction$

Diese Gleichung gibt die Grundlage für eine untere Grenze von α an. Solange diese Bedingung erfüllt ist, ist das Regelungssystem stabil. Weil R_A und C_F als RC-Filter eine Lastspitze dämpfen, wird die Lastspitze mit einem sehr großen Wert von α gedämpft. Deshalb sollte der Wert von α nicht zu groß sein. In einem praktischen Design sollte der Parameter α um 20 bis 30 Prozent größer als der untere Grenzwert sein.

Schleifenkompensation und Designbeispiel

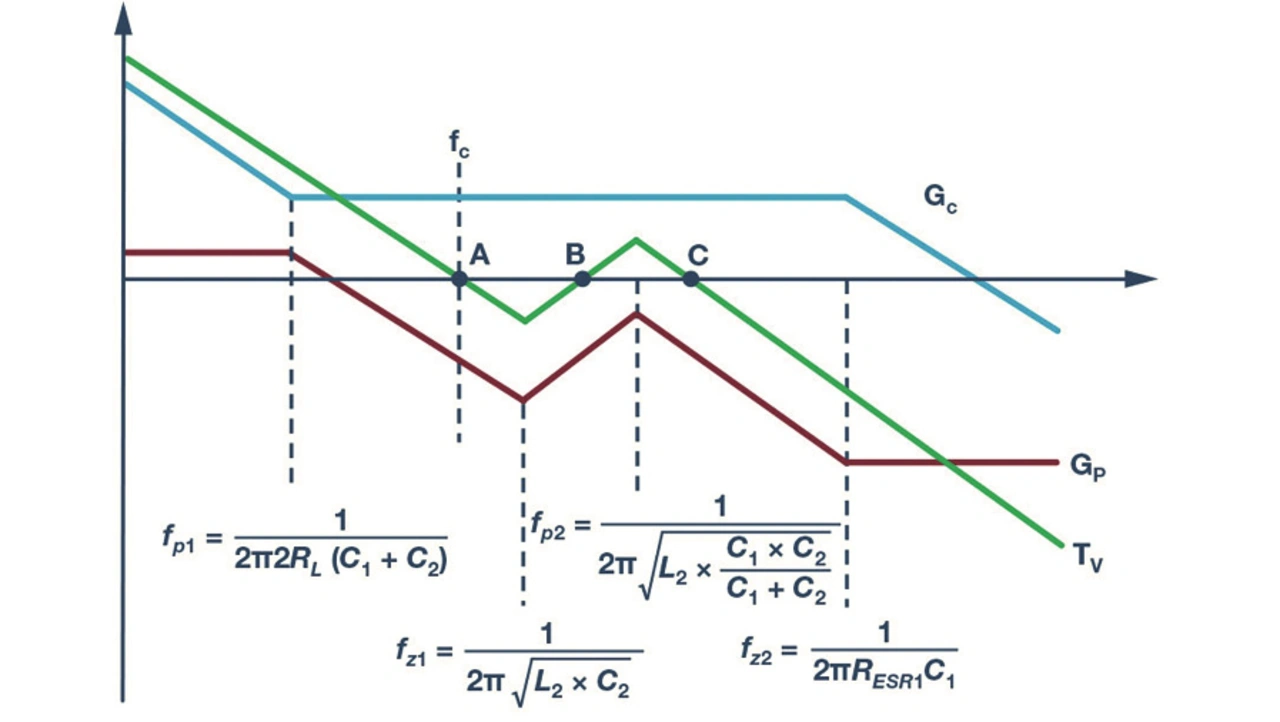
Die Übertragungsfunktion von der Regelung zur Rückkopplung G_P(s) lässt sich aus dem Produkt der Übertragungsfunktion von der Regelung zum Ausgang G_vc(s) und der Übertragungsfunktion der Rückkopplung G_FB(s) ableiten. Die Übertragungsfunktion der Kompensation G_C(s) ist so ausgelegt, dass sie eine Null- und eine Polstelle hat. Das asymptotische Bode-Diagramm von G_P(s) und G_C(s) sowie der Übertragungsfunktion der geschlossenen Regelschleife T_v(s) sind in Bild 9 dargestellt.

Die folgenden Abläufe zeigen, wie man die Kompensations-Übertragungsfunktion bildet:

Bestimmen der Durchtrittsfrequenz f_c. Da die Bandbreite bei f_z1 begrenzt ist, wird empfohlen, dass f_c kleiner sein soll als f_z1.
Berechnen der Verstärkung von G_P(s) bei f_c, dann sollte die Verstärkung des Mittenfrequenzbandes von G_C(s) gegenüber von G_P(s) liegen.
Platzieren der Kompensations-Nullstelle an der Frequenz der Polstelle der Leistungsstufe f_p1.
Platzieren der Kompensations-Polstelle an der Frequenz der Nullstelle f_z2, die vom ESR des Ausgangskondensators C₁ erzeugt wird.

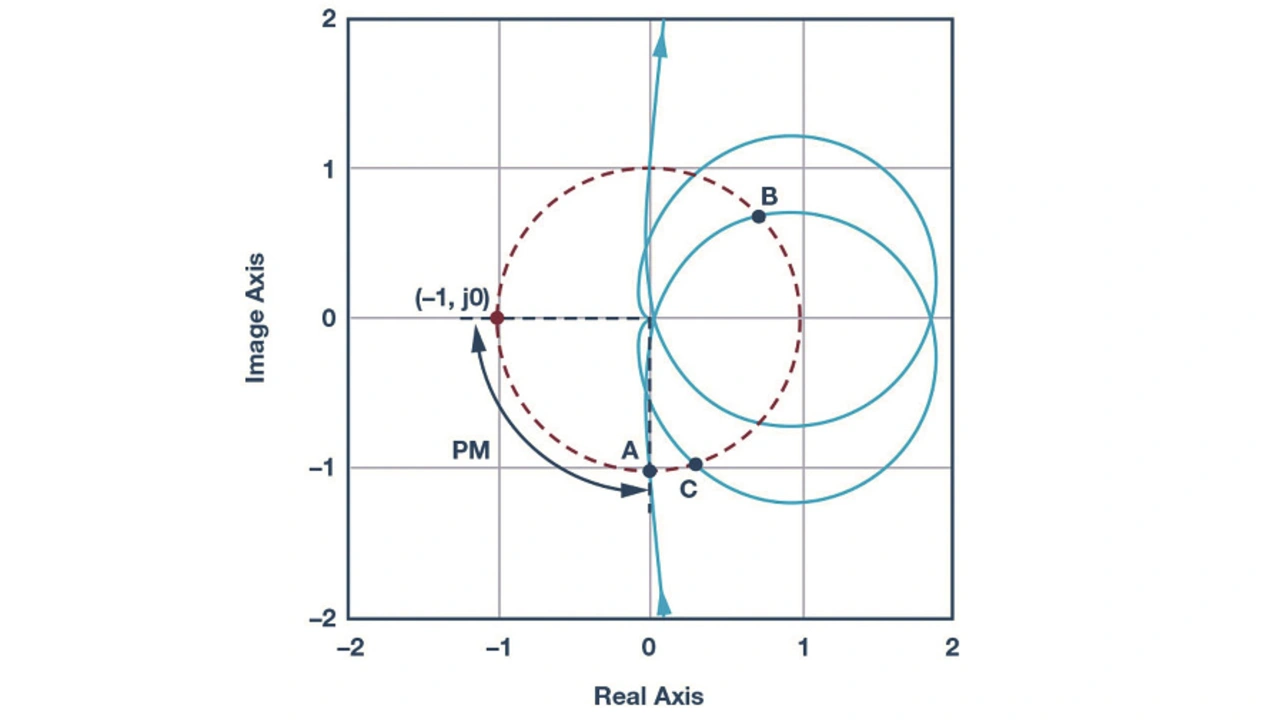
Nach Bild 8 kreuzt die Übertragungsfunktion des geschlossenen Regelkreises T_v(s) die Nulllinie dreimal. Mithilfe eines Nyquist-Diagramms lässt sich die Stabilität dieser Übertragungsfunktion analysieren (Bild 10). Da diese Kurve weit von (–1, j0) entfernt ist, ist der geschlossene Regelkreis stabil und die Phasenreserve groß genug. Man beachte, dass die Punkte A, B und C im Nyquist-Diagramm mit den Punkten A, B und C im Bode-Diagramm korrespondieren.

Der Schaltregler-IC ADP5014 von Analog Devices optimiert viele analoge Funktionsblöcke, um im niederfrequenten Bereich ein geringeres Rauschen zu erzielen. Die Struktur der Referenzspannung mit Verstärkungsfaktor 1 (Unity Gain) macht das Ausgangsrauschen ebenfalls unabhängig von der Einstellung der Ausgangsspannung, wenn diese auf niedrigere Werte eingestellt wird als die Referenzspannung. Ein zweites LC-Filter wird hinzugefügt, um das Ausgangsrauschen bei hohen Frequenzen zu dämpfen, insbesondere bei der Grundfrequenz des Schaltreglers und ihren Harmonischen. Bild 11 zeigt die Details des Designs.

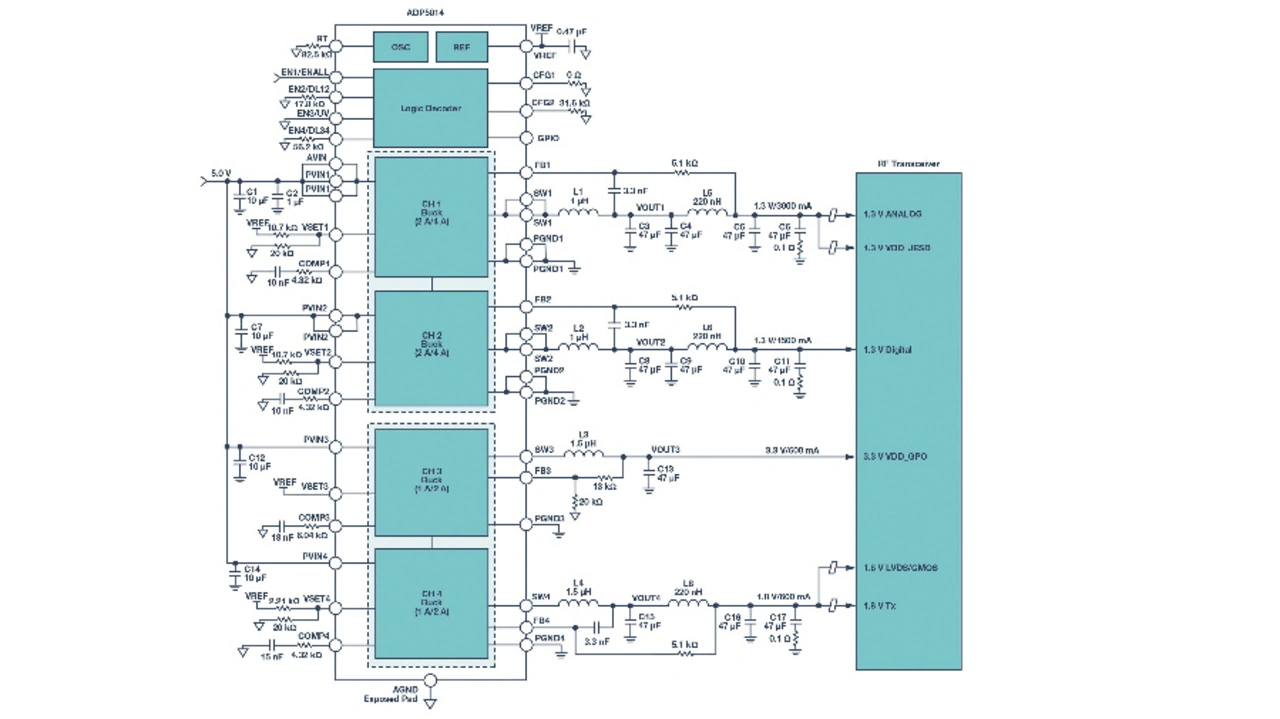
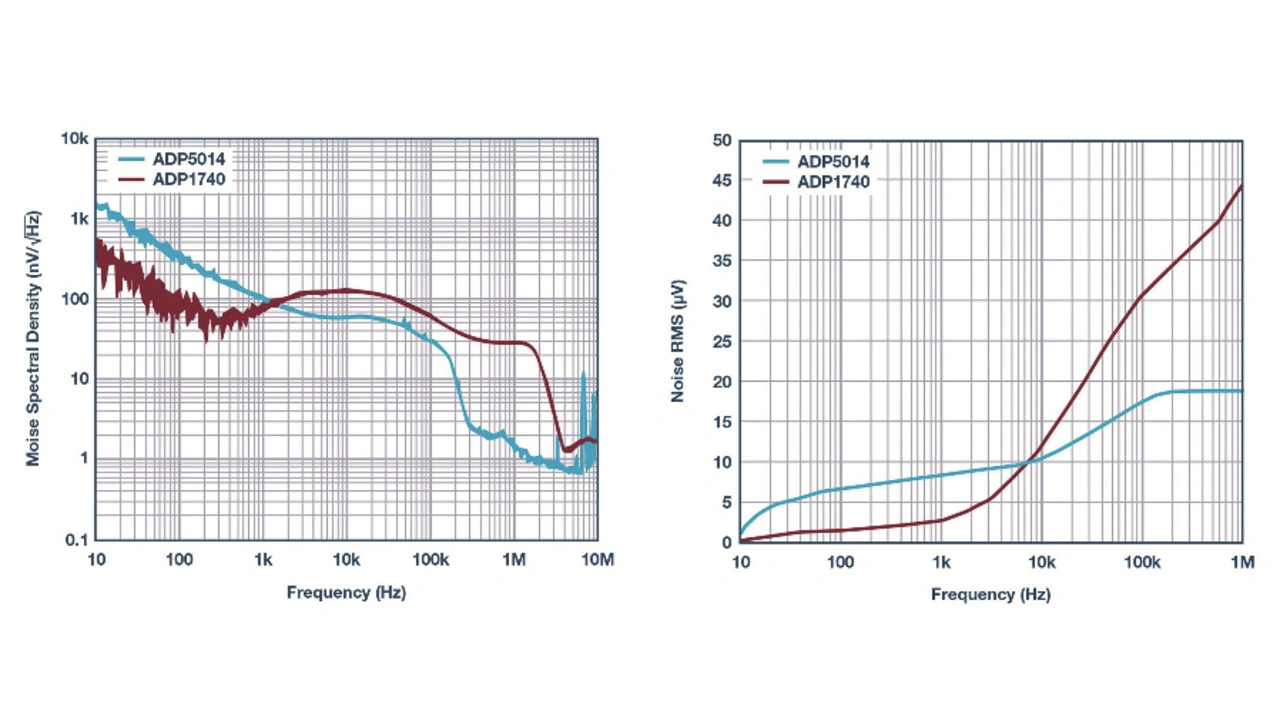
Bild 12 zeigt die gemessene spektrale Rauschdichteverteilung des ADP5014 im Frequenzbereich von 10 Hz bis 10 MHz und die integrierte RMS-Rauschdichteverteilung im Bereich zwischen 10 Hz und 1 MHz im Vergleich zum ADP1740, einem rauscharmen 2-A-Linearregler. Das Ausgangsrauschen des Schaltreglers ADP5014 ist im HF-Bereich deutlich besser als das des linearen ADP1740.

Die Modellierung und Regelung in diesem Beitrag konzentrierten sich auf einen Current-Mode-Abwärtswandler, aber die beschriebene Methode lässt sich auch für Voltage-Mode-Abwärtswandler einsetzen.

REFERENZEN

[1] Ray Ridley: A New, Continuous-Time Model for Current-Mode Control; IEEE Transactions on Power Electronics, Vol. 6, No. 2, 1991; DOI: 10.1109/63.76813.

[2] Julie Yixuan Zhu, and Brad Lehman: Control Loop Design for Two-Stage DC-to-DC Converters with Low Voltage/High Current Output; IEEE Transactions on Power Electronics, Vol. 20, No. 1, 2005; DOI: 10.1109/APEC.2003.1179317.

[3] Patricio Cortes, David O. Boillat, Hans Ertl, and Johann W. Kolar: Comparative Evaluation of Multiloop Control Schemes for a High Bandwidth AC Power Source with a Two-Stage LC Output Filter; International Conference on Renewable Energy Research and Applications, IEEE, 2013; DOI: 10.1109/ICRERA.2012.6477339.

[4] Ray Ridley: Secondary LC Filter Analysis and Design Techniques for Current-Mode-Controlled Converters; IEEE Transactions on Power Electronics, Vol. 3, No. 4, 1988; DOI: 10.1109/63.17972.

[5] Byungcho Choi, Bo H. Ch, Fred C. Lee, and Ray Ridley: Three-Loop Control for Multimodule Converter Systems; Power Electronics IEEE Transactions on Power Electronics, Vol. 8, No. 4, 1993; DOI: 10.1109/63.261017.

[6] Herleitungen Teil 1

[7] Herleitungen Teil 2