Startseite > Power > Peak-Current-Mode-Regler

Regelungstechnik – Teil 6 von 6

Peak-Current-Mode-Regler

19. März 2020, 14:30 Uhr | Von Dr. Ali Shirsavar, Dr. Michael Hallworth und Florian Hämmerle

▶ Diesen Artikel anhören

Fortsetzung des Artikels von Teil 1

Schritt 2: Bode-Diagramm der Regelstrecke ermitteln

Die graphische Darstellung ist zwar nicht zwingend erforderlich, dennoch ist ein Visualisieren der Vorgänge hilfreich. Es gibt viele Modelle für Peak-Current-Mode-Wandler. Hier wird das beliebte Ridley-Modell verwendet. Detaillierte mathematische Analysen und Gleichungen sind in [2 ]und [3] zu finden.

Bild 3 zeigt das Bode-Diagramm des PCMR-Tiefsetzstellers. Bei niedrigen Frequenzen ist die DC-Verstärkung ersichtlich. Es existiert eine niederfrequente reale Polstelle, eine ESR-Nullstelle und ein komplex konjugiertes Polstellenpaar bei halber Schaltfrequenz. Dieser Kurvenverlauf ist für alle hart schaltenden Eintaktflusswandler ähnlich. Zwar unterscheiden sich die niederfrequente Polstelle und die ESR-Nullstelle der Regelstrecke, das komplex konjugierte Polstellenpaar wird jedoch immer bei der halben Schaltfrequenz zu finden sein.

Die gestrichelte grüne Linie zeigt die komplex konjugierten Polstellen bei halber Schaltfrequenz ohne Anstiegskompensation. Bei höherem Tastgrad wäre die Spitze beziehungsweise der Peak deutlicher ausgeprägt. Wie die Resonanzüberhöhung mit der in Schritt 1 berechneten Anstiegskompensation gedämpft wird, zeigt die durchgezogene Linie. Im Gegensatz zur im vorangegangen Beitrag erläuterten Voltage-Mode-Regelung, ist die Übertragungsfunktion der Regelstrecke wesentlich einfacher geworden.

Schritt 3: Pol- und Nullstellen des Typ-II-Reglers berechnen

Die hier vorgestellte Methode stellt eine einfache Annäherung dar, um die Pol- und Nullstellen für einen leistungsfähigen Regler samt angemessener Durchtrittsfrequenz (ein Zehntel der Schaltfrequenz) zu berechnen. Die hier verwendete Software zur Netzteil-Auslegung (Biricha WDS) nutzt optimale Algorithmen, in dem kurzen Beitrag wird jedoch eine Näherungsmethode zum Berechnen per Hand vorgestellt.

Aus der Übertragungsfunktion des Reglers ist ersichtlich, dass es lediglich eine Polstelle, eine Nullstelle und einen Integrator (Polstelle im Ursprung) gibt. Folgende Schritte führen zu gutem dynamischem Verhalten und ausreichend Stabilität:

a) Platzieren einer Regler-Polstelle bei der Frequenz der ESR-Nullstelle um sie zu kompensieren:

$f subscript p 1 equals end subscript fraction numerator 1 over denominator 2 pi E S R times C end fraction equals 11 comma 6 k H z space space space$

b) Platzieren der Regler-Nullstelle bei einem Fünftel der gewünschten Durchtrittsfrequenz um eine Phasenanhebung in dem Bereich zu erhalten. Unsere gewünschte Durchtrittsfrequenz Fx ist in dem Fall 10 kHz:

$f subscript z 1 end subscript equals F subscript x over 5 equals 2 k H z space space space space$

c) Der Integrator (Position der Polstelle im Ursprung) und die Koeffizienten A1, A2 und A3 bestimmen sich wie folgt:

$A subscript 1 equals 1 comma 23 F subscript x R subscript i open parentheses L plus fraction numerator R subscript L T subscript s over denominator pi end fraction close parentheses A subscript 2 space equals square root of 1 minus 4 F subscript x superscript 2 T subscript s superscript 2 end root plus 16 F subscript x superscript 4 T subscript s superscript 4 A subscript 3 space equals space square root of 1 plus fraction numerator 4 pi squared C squared F squared L squared R subscript L superscript 2 over denominator left parenthesis L pi plus R subscript L T subscript s right parenthesis end fraction end root$

Schritt 4: Bauteilwerte des Reglers berechnen

Nun sind die Positionen der Pol- und Nullstellen unseres Reglers bekannt. Somit sind mit den Gleichungen 2 die Komponentenwerte für den Regler zu berechnen.

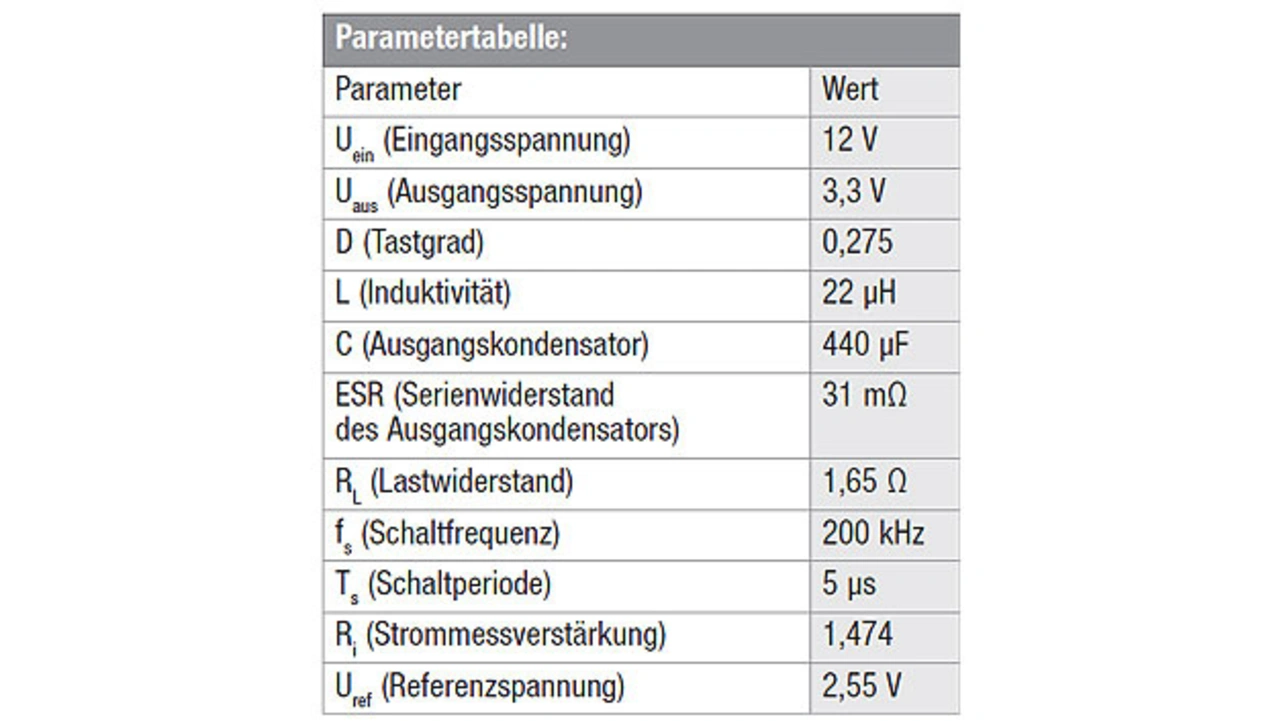
Wie bereits im vorangegangen Beitrag über den Voltage-Mode-Regler erläutert, sind R₁ und R_b basierend auf der Stromstärke und der für den integrierten Regler-IC benötigten Referenzspannung (in diesem Fall 2,55 V) zu berechnen. Mit einer Stromstärke von 1 mA, die über den Spannungsteiler fließen soll, ergeben sich:

R₁ = 750Ω

R₂ = 2,55kΩ

Die Gleichungen 2 können umgestellt werden, sodass C1, C3 und R2 wie folgt zu berechnen sind:

$C subscript 1 space equals space fraction numerator omega subscript p 1 space minus omega subscript z 1 end subscript end subscript over denominator R subscript 1 omega subscript p 0 end subscript omega subscript p 1 end subscript end fraction space equals space 6 comma 8 n F C subscript 1 space equals space fraction numerator omega subscript z 1 end subscript over denominator R subscript 1 omega subscript p 0 end subscript omega subscript p 1 end subscript end fraction space equals space 1 comma 4 n F R subscript 2 space equals space fraction numerator R subscript 1 omega subscript p 0 end subscript omega subscript p 1 over denominator left parenthesis omega subscript p 1 end subscript minus omega subscript z 1 end subscript right parenthesis omega subscript z 1 end subscript end fraction space equals space 11 comma 7 k capital omega$

Die Software WDS kann im Modus »manual pole/zero placement« (manuelle Platzierung von Pol-/Nullstellen) verwendet werden, um die Berechnungen zu überprüfen. WDS liefert alle wichtigen Stabilitätsparameter sowie das Bode-Diagramm – das aus dem WDS stammende Bode-Diagramm ist in Bild 4 dargestellt.

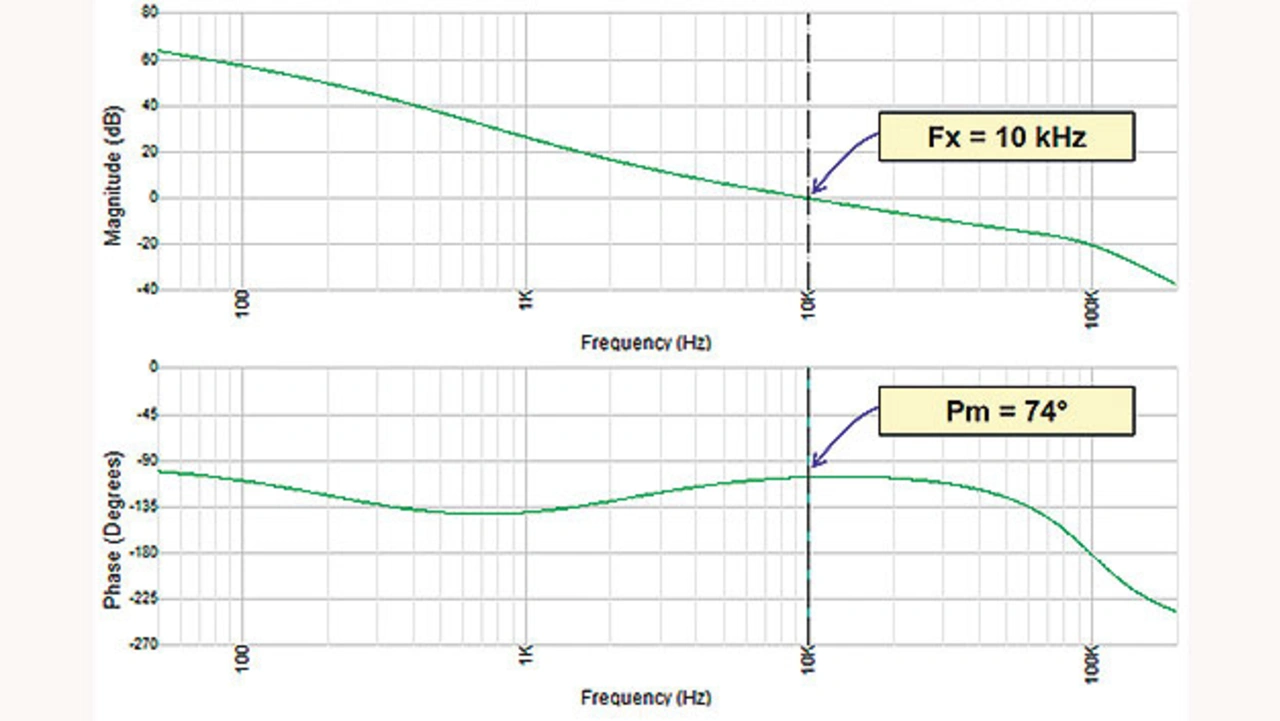
Aus Bild 4 ist ersichtlich, dass die angestrebte Durchtrittsfrequenz von 10 kHz und eine hohe Phasenreserve von 74° erreicht wurde. Der Anstieg bei Durchtrittsfrequenz beträgt -20 dB pro Dekade und die Amplitudenreserve ist größer als 20 dB. Somit wurde ein äußerst stabiles Netzteil mit einer respektablen Durchtrittsfrequenz und einer großen Phasenreserve entworfen.

Schnelle Berechnung des Reglers

Mit dem vorgestellten Näherungsverfahren lassen sich in den meisten Fällen zufriedenstellende Ergebnisse erzielen. Der Vorteil der hier vorgestellten Methode liegt in der schnellen Berechnung. Ein Nachteil ist hingegen die fehlende Kontrolle über die Phasenreserve. Ein anschauliches Rechenbeispiel bis hin zur Wahl der Komponentenwerte zeigte beispielhaft, wie sich ein Peak-Current-Mode-Regler aufbauen lässt.

Literaturverzeichnis

[1] Biricha Digital’s Analog Power Supply Design Workshop Manual.
[2] Ridley, R.B.: A New Continuous-Time Model for Current-Mode Control. IEEE Transactions on Power Electronics. April 1991. S. 271-280.
[3] Microcontroller Based Peak Current Mode Control. PhD Thesis. M. Hallworth.

Die Autoren