Startseite > Messen + Testen > Elektromagnetische Kopplung und Signalzusammensetzung

Phänomene in der EMV

Elektromagnetische Kopplung und Signalzusammensetzung

16. April 2018, 6:30 Uhr | Von Dr. Heinz Zenkner

▶ Diesen Artikel anhören

Fortsetzung des Artikels von Teil 2

Signalzusammensetzung

Die Takt- und Signalfrequenzen elektronischer Produkte werden höher, die Signalpegel und Betriebsspannungen nehmen hingegen ab. So tendieren die von elektronischen Produkten abgestrahlten Störungen zu höheren Frequenzbereichen. Die Störfestigkeit jedoch nimmt ab, da der Störabstand zwischen Signalamplitude und gekoppeltem Störsignal geringer wird. Zudem wird, auf einen Zeitabschnitt betrachtet, durch die wesentlich höheren Datenraten pro Störintervall mehr Datenvolumen gestört. Daten- und Signalverarbeitungsprozesse laufen heute fast nur noch mit digitalen Signalen ab, die Zeit der Analogtechnik ist vorbei. Somit macht es Sinn, sich mit der Zusammensetzung digitaler Signale zu befassen.

Jobangebote+ passend zum Thema

Ingenieur/Elektroingenieur/Elektrotechniker als Field Application Engineer

GEYER Electronic GmbH, Planegg

Alle Jobangebote im Elektroniknet Karrierebereich anzeigen

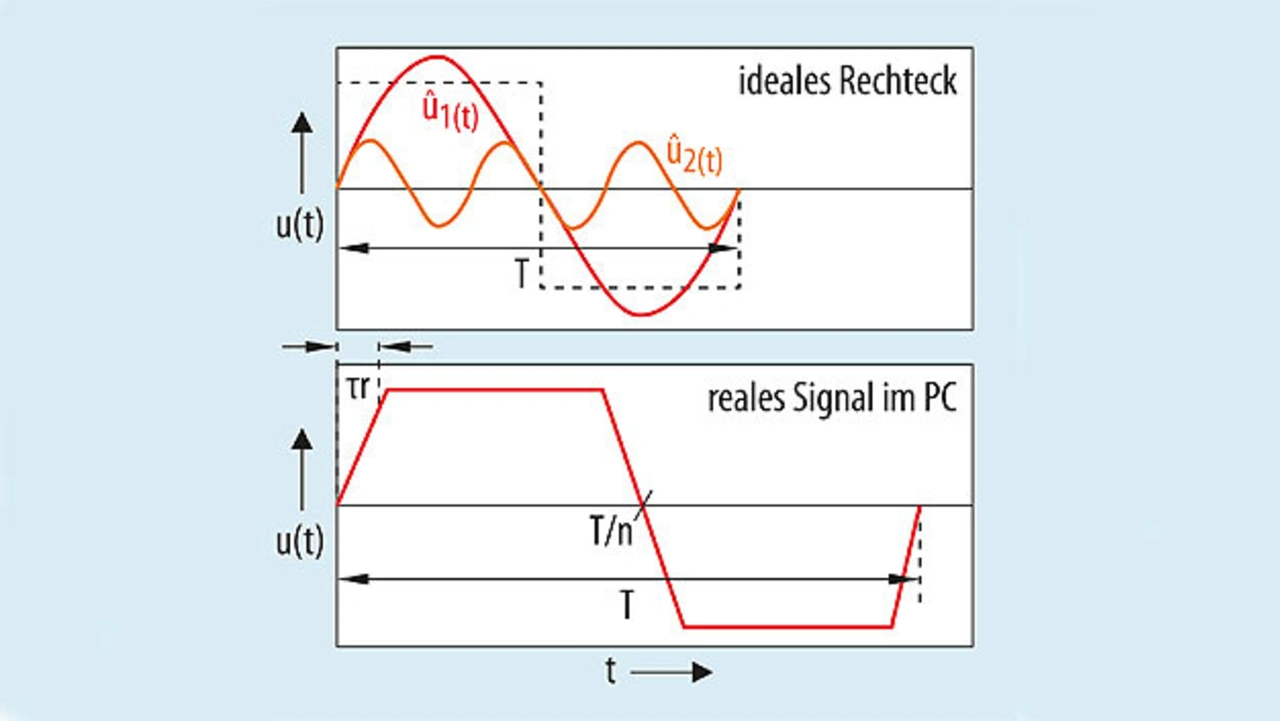
Digitale Signale, »Rechtecksignale« setzen sich aus einzelnen sich nach Betrag und Phase addierten sinusförmigen Signalanteilen zusammen, wie das in Bild 10 dargestellt ist.

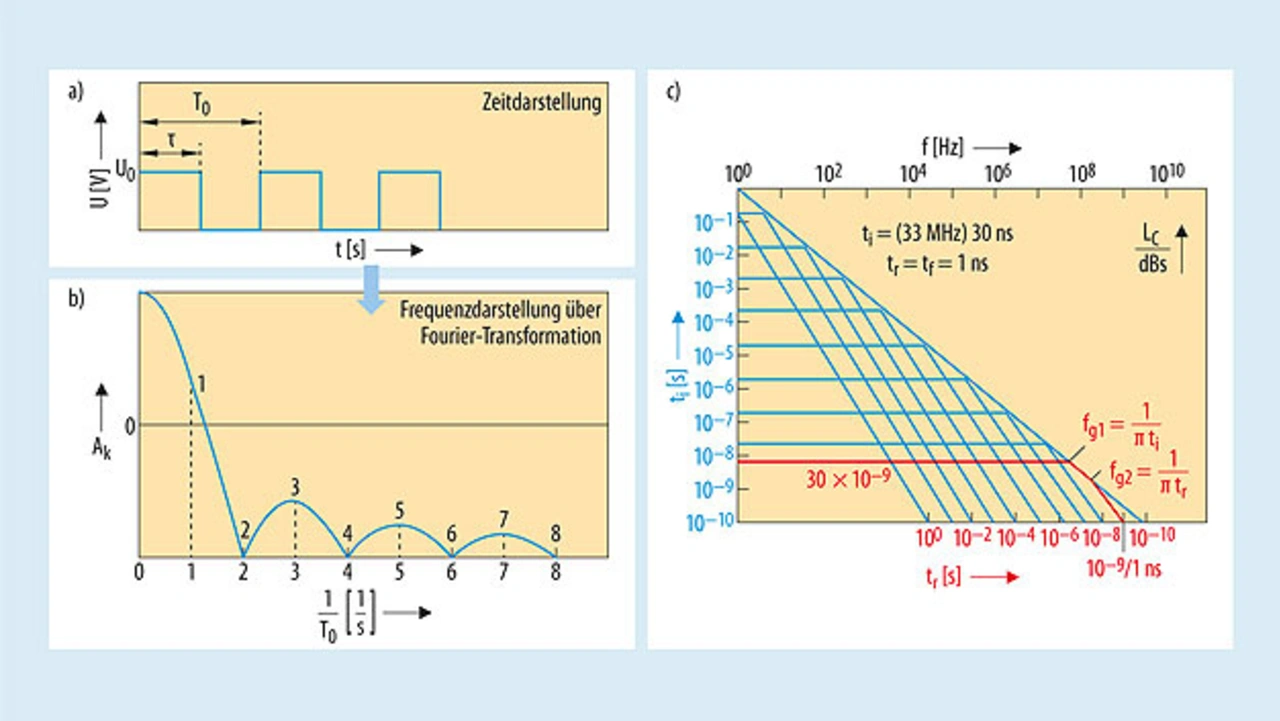
Abhängig von der Periodendauer und der Flankenanstiegszeit des Rechtecksignals, erstrecken sich die Frequenzen der harmonischen Signale bis in den GHz-Bereich. Die Amplitude der Harmonischen nimmt mit zunehmender Frequenz ab, diesen Verlauf zeigt Bild 11.

Es lässt sich zeigen, dass ab einer Eckfrequenz von f_g1 = 1/πti die Amplitude der Harmonischen mit 20 dB/dek abnimmt, ab der Eckfrequenz f_g2 = 1/πt_r mit 40 dB/dek, t_i ist dabei die Impulsdauer und tr die Flankenanstiegszeit. So lässt sich mit einer relativ einfachen Signalanalyse mit einem Oszilloskop der Anteil der Harmonischen ermitteln.

Natürlich bieten moderne Oszilloskope auch die Möglichkeit, eine Fast-Fourier-Analyse von dem entsprechenden Signal durchzuführen; die angenehmste und genaueste Lösung ist aber der Einsatz eines Spektrumanalysators mit entsprechendem hochimpedantem Tastkopf.

Allgemein lässt sich zu den Signalen anmerken, dass alle nichtperiodischen Signale wie z.B. Video- und Datensignale aufgrund ihrer hohen Bandbreite kein so hohes Störpotenzial haben (Energie pro Bandbreite), schmalbandige Signale wie z.B. Taktsignale haben hingegen ein hohes Störpotenzial, da die gesamte Energie des Signals auf das schmale Frequenzfenster begrenzt ist.

Die Kopplung von Störsignalen lässt sich in der Praxis durch eine Funktion (K) beschreiben, die proportional zur Frequenz (K ~ f) verläuft.

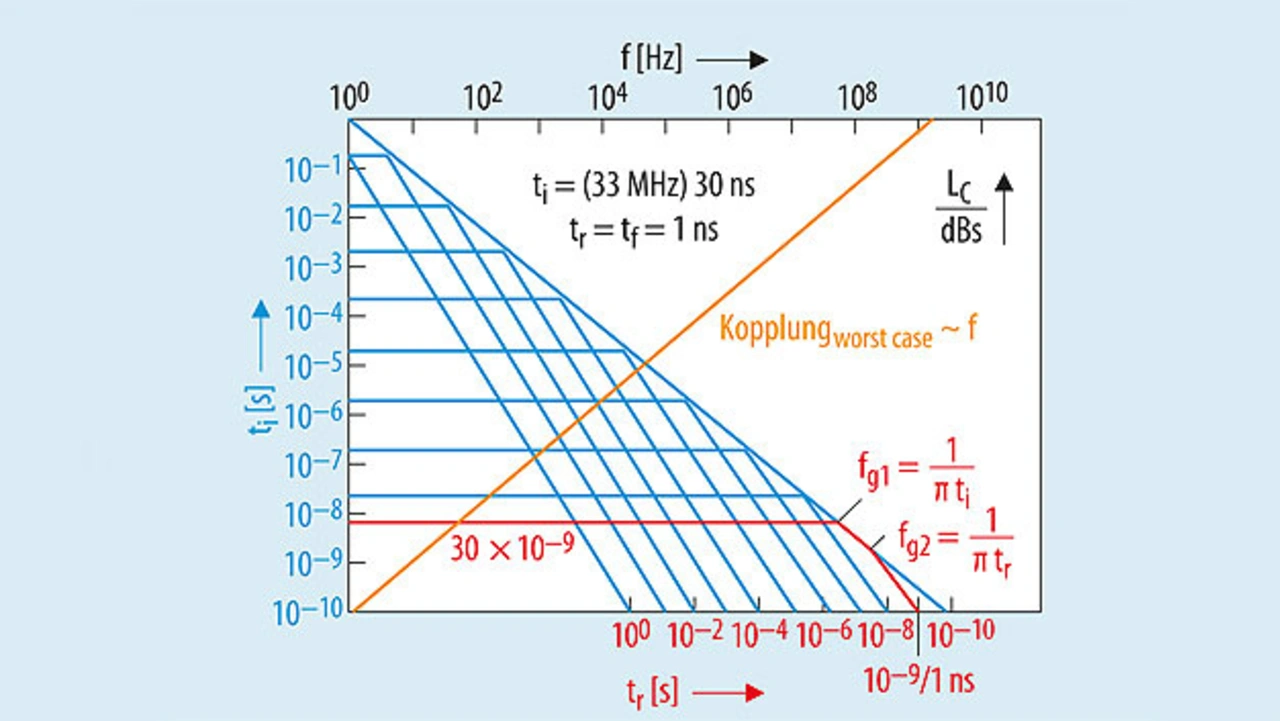
Wird die Kopplungsfunktion mit dem Signalverlauf nach Bild 11 verknüpft, ergibt sich im Frequenzbereich der Zusammenhang, wie er in Bild 12 verdeutlicht ist.

Die Kurven (blau und orange) in Bild 12 müssen grafisch addiert werden um die entsprechende Darstellung der Amplituden des Signals an der Störsenke zu erhalten. Somit ergibt sich an der Störsenke folgendes Bild (Bild 13).

Im Frequenzbereich von 0 bis f_g1 ist der Amplitudenverlauf des Störsignals linear, zwischen f_g1 und f_g2 sinken die Amplituden der Harmonischen mit 20 dB/dek und im Bereich darüber mit 40 dB/dek.

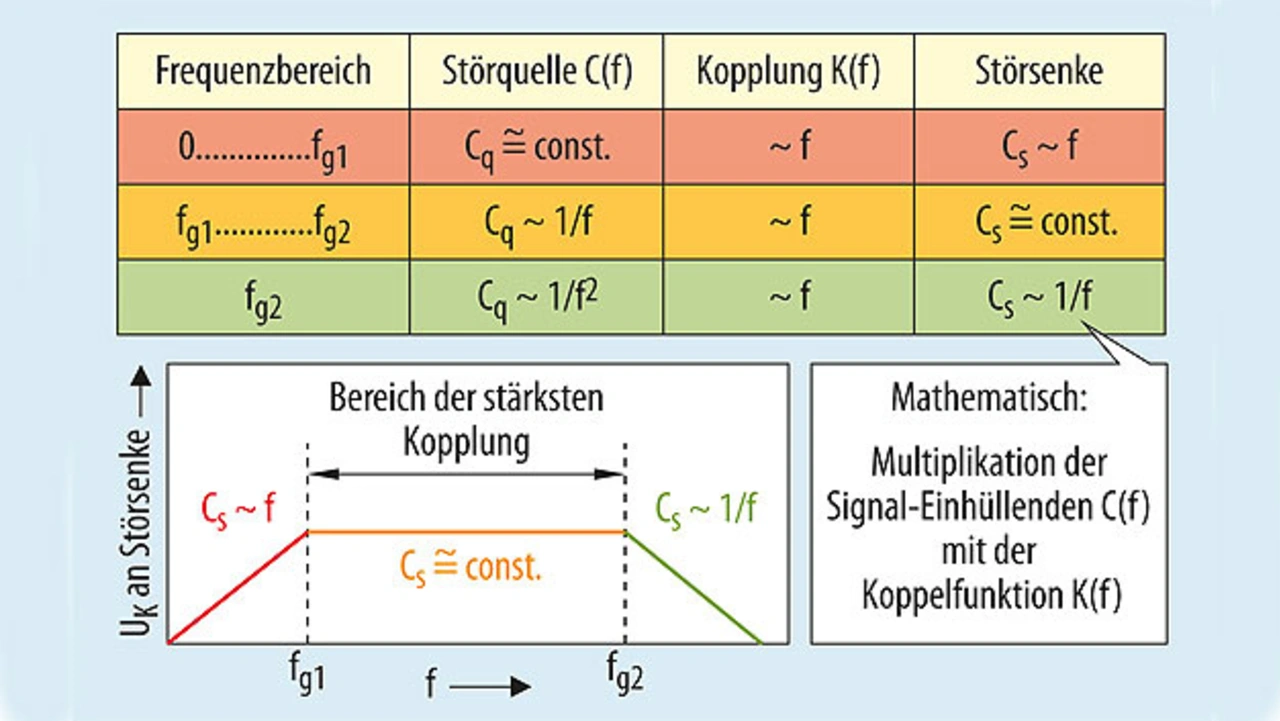
Da der Verlauf der Koppelfunktion mit 20 dB/dek. steigt, ergibt sich für den Signalpegel an der Störsenke der Zusammenhang, wie er in Bild 13 unten dargestellt ist.

Das bedeutet, dass die Relevanz der Signal- bzw. Störsignalharmonischen sich zu höheren Frequenzen in den Bereich zwischen f_g1 und f_g2 verschiebt. Dort sind also die wirkungsvollsten Störeinflüsse zu erwarten.

Der Autor

Dr. Heinz Zenkner

hat Elektrotechnik mit Schwerpunkt Hochfrequenztechnik studiert und im Fachbereich Hochfrequenztechnik promoviert. Er ist seit vielen Jahren öffentlich bestellter und vereidigter Sachverständiger für EMV. Neben zahlreichen wissenschaftlichen Veröffentlichungen tritt Dr. Zenkner auch als Autor in einer Vielzahl von Werken zur EMV in Erscheinung.

In seiner beruflichen Laufbahn hat er als Dozent an verschiedenen Universitäten gearbeitet und Seminare an der IHK geleitet. Seit vielen Jahren beschäftigt er sich mit industrieller Elektronik, von der ersten Idee eines Produktes bis hin zur Serienproduktion.