Startseite > Kommunikation > Wireless > Vergleich der Reichweiten

Low Power Wide Area Network

Vergleich der Reichweiten

14. August 2017, 11:00 Uhr | Von Harald Naumann

▶ Diesen Artikel anhören

Fortsetzung des Artikels von Teil 1

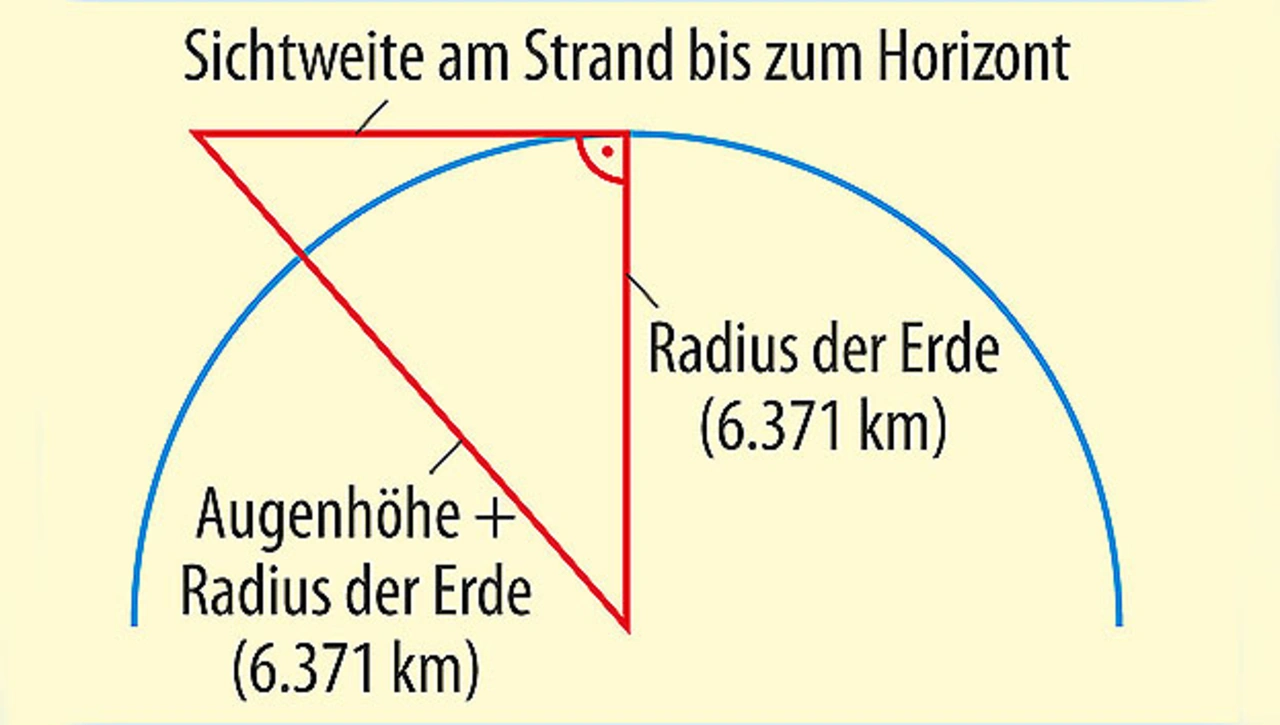
Sichtweite zum Horizont am Strand

Bei 1,7 m Augenhöhe ist es am Strand möglich, 4,7 km weit zu blicken. Der Grund dafür wurde bereits vor hunderten von Jahren von Nikolaus Kopernikus ermittelt.

Die Erde ist keine Scheibe, sondern ein Ellipsoid mit einem mittleren Radius von 6371 km. In der Schifffahrt ist das Problem auch bekannt. Wer einen Segelschein macht, muss sich mit der Tragweite des Lichts beschäftigen (Bild 3). Die Sichtweite (s) lässt sich nach der folgenden Gleichung berechnen:

$S equals square root of open parentheses r subscript E r d e end subscript plus h close parentheses end root squared minus r subscript E r d e end subscript superscript 2$

Um die anfangs erwähnten 15 km weit sehen zu können, muss der Betrachter bei 1,7 m Augenhöhe auf einer 16 m hohen Plattform stehen, um damit die Augenhöhe von 17,7 m zu erzielen. Denn mit 17,7 m Augenhöhe lässt es sich 15 km weit schauen.

Mobilfunk-Basisstationen (LTE) werden im Stadtgebiet auf einer Höhe von ca. 30 m geplant. Bei 30 m Augenhöhe lässt sich am Strand bereits 19,6 km weit übers Meer bis zum Horizont blicken (Tabelle 1).

Augenhöhe am Strand [m]	Sichtweite [km]
1,7	4,7
17,7	15,0
20,0	19,6

Tabelle 1. Soweit das Auge reicht. Die Sichtweite endet spätestens am Horizont. Nur für den, der höher steht, vergrößert sich die Sichtweite, der Horizont liegt weiter weg.

Der Horizont ist aber nur eine der Begrenzungen für eine Funkwelle bei 868 MHz bzw. bei LTE-Cat-NB1 im Bereich von 800 bis 960 MHz. Die quasioptische Ausbreitung gilt für Funkwellen im Bereich von Sub-GHz nicht. Im nächsten Schritt wird daher die Wellenausbreitung im flachen Land betrachtet – mit Hilfe des Egli-Modells – und dann in urbanen Bereichen – mit dem Hata-Okumura-Modell, kurz Hata-Modell genannt.

Bestimmung der Reichweite auf Basis des Egli-Modells

John Egli hat in den 1950ern die Feldstärke am Empfänger in Entfernung zum Sender ermittelt und daraus eine Formel zur Berechnung der Dämpfung (D) auf dem Übertragungsweg abgeleitet [1].

$D equals thin space G subscript s times G subscript E space times space open parentheses fraction numerator h subscript S times space h subscript E space over denominator d squared end fraction close parentheses times beta$

mit:

d = Distanz zwischen Sender und Empfänger
G_S= Gewinn der Senderantenne
G_E = Gewinn der Empfängerantenne
h_S = Höhe der Senderantenne
h_E = Höhe der Empfängerantenne
β = (40/f)², mit f = Sendefrequenz in MHz

Die Formel lässt sich vereinfachen, wenn Antennen ohne Gewinn verwendet werden:

$D equals 40 log open parentheses d close parentheses minus space 20 log open parentheses h subscript s close parentheses minus space 20 log open parentheses h subscript E close parentheses minus space 10 log open parentheses beta close parentheses$

In dieser Formel wird die Reichweite durch drei Parameter bestimmt: die Höhe der Sendeantenne, die Höhe der Empfängerantenne und die Sendefrequenz. Wird das Modell von Egli anwendet und die Höhe des IoT-Gerätes auf 1 m gesetzt, dann errechnet sich mit einer Leistungsübertragungsbilanz von 151 dB, für eine gewünschte Reichweite von 15 km eine Höhe von 140 m für den Sendemast. Dieser müsste noch dazu in einer Ebene wie der Lüneburger Heide stehen. Das höchste Gebäude inmitten der Landeshauptstadt Hannover ist im Besitz der Stadtwerke und hat eine Höhe von 92 m. Mit einer auf diesem Gebäude montierten Sendeantenne lässt sich nach Egli nur eine Reichweite von 12 km errechnen – wenn das Gebäude in einer wenig bebauten ebenen Landschaft stehen würde und nicht mitten in einer Großstadt. Sollen gar 48 km Reichweite erzielt werden, müsste nach dem Modell von Egli die Sendeantenne bei gleicher Leistungsübertragungsbilanz von 151 dB auf einem 1400 m hohen Turm installiert werden.

Türme und Gebäude in der Höhe von 140 m oder gar 1400 m sind nicht nur in Niedersachsen dünn gesät. Das höchste Gebäude der Erde ist derzeit mit 828 m der Wolkenkratzer Burj Khalifa in Dubai. Im platten Land sind, mangels Türmen, Gebäuden oder Bergen mit der nötiger Höhe, Reichweiten von 15 km mit einer Leistungsübertragungsbilanz von 151 dB unmöglich zu realisieren, und die mystischen 48 km lassen nicht einmal am Persischen Golf erreichen.

Bestimmung der Reichweite auf Basis des Hata-Modells

Das Modell von Egli ist für die Planung im städtischen Bereich nicht brauchbar. Für Städte eignet sich das Hata-Modell besser, das im Jahr 1968 in Japan ermittelt wurde und auch heute noch für städtische Umgebungen Gültigkeit hat [2]. Das Hata-Modell unterscheidet durch verschiedene Terme in der Dämpfungsformel die Flächennutzung – von unbebauten Flächen bis hin zu dicht bebautem Stadtgebiet.

$D space equals space 69 comma 55 plus 26 comma 16 log left parenthesis f right parenthesis minus space 13 comma 82 log open parentheses h subscript s close parentheses plus space open square brackets 44 comma 9 minus 6 comma 55 log left parenthesis h subscript s right parenthesis close square brackets times log open parentheses d close parentheses minus K$

mit:
d = Distanz zwischen Sender und Empfänger
h_S = Höhe der Senderantenne
h_E = Höhe der Empfängerantenne
K = Konstante für Art der Stadt und Bebauung

unbebaut: K = 4,78 ×(log(f²) – log(f) + 40,94
Vorstadt: K = 2 × log(f/28)2 + 5,4
Kleinstadt: K = (1,1 × log(f) – 0,7) × h_E – (1,56 × log(f) – 0,8)
Großstadt, f < 300 MHz: K = 8,29 × (log(1,54 × h_E))² – 1,1
Großstadt, f > 300 MHz: K = 3,2 × (log(11,7555 × h_E))² – 4,97

f = Sendefrequenz

Für die folgende Reichweitenbetrachtung wird mit einer Dämpfung von 20 dB für die Gebäudedurchdringung und einem Verlust von 8 dB für Fading gerechnet. Damit erfolgt eine Anpassung an die Bedingungen beim Fernauslesen von elektronischen Zählern – einem der wichtigen Zielmärkte für LPWAN. In Deutschland sind Zähler im Allgemeinen in den Gebäuden montiert. Die Leistungsübertragungsbilanz wird also für den Vergleich der Reichweite in dicht bebauter Umgebung bei allen LPWAN-Techniken um 28 dB reduziert.

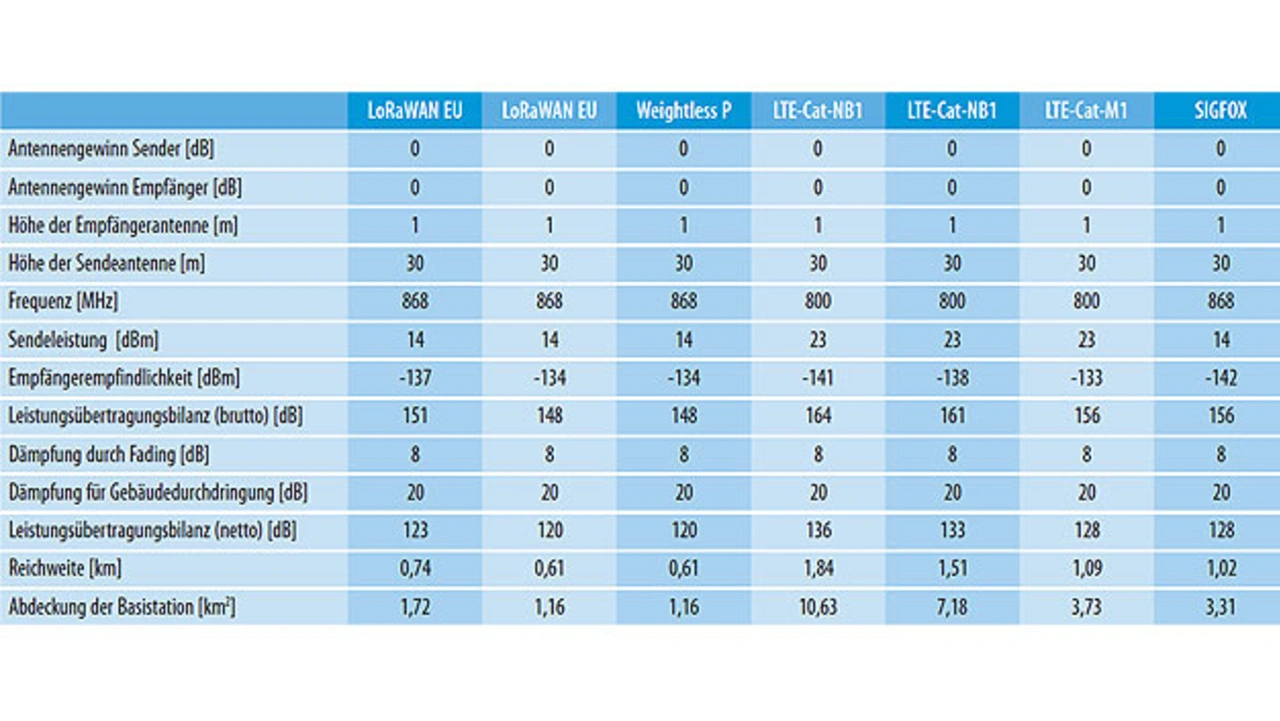
Die Tabelle 3 zeigt die Reichweite von Basisstationen (BTS – Base Transceiver Station) für die verschiedenen LPWAN-Funktechniken. Da die Fläche eines Kreises mit r² × π bestimmt wird, nimmt die Fläche der Abdeckung im Quadrat der Reichweite zu. Um den Unterschied von 3 dB zu verdeutlichen, ist LoRaWAN in der Tabelle 3 mit 151 dB und mit 148 dB für die Leistungsübertragungsbilanz eingetragen. Mit dem Wert 148 dB erreicht LoRaWAN die gleiche Reichweite wie Weightless P.

Die 50 bit/s mit einer Leistungsübertragungsbilanz von 164 dB sind bei LTE-Cat-NB1 nicht praktikabel. Daher ist LTE-Cat-NB1 auch noch mit einer Datenrate von ca. 600 bit/s und 161 dB Leistungsübertragungsbilanz in Tabelle 3 aufgeführt. LTE-Cat-NB1 bietet bei 161 dB Leistungsübertragungsbilanz ähnliche Datenraten wie LoRaWAN und Weightless P – bietet allerdings eine viel höhere Reichweite. Sigfox wurde zur Vollständigkeit hinzugefügt. Sigfox arbeitet mit unidirektionalen Antennen mit zu 3 bis 5 dB Gewinn. Dieser Antennengewinn wurde in der Tabelle 3 bereits zum Empfindlichkeitswert addiert. Wenn Antennen mit Gewinn bei Weightless P zum Einsatz kommen, dann lässt sich eine Leistungsübertragungsbilanz ähnlich wie bei Sigfox erreichen.