Multi-Gigahertz-Taktbäume
Neun Tipps zum Minimieren von Laufzeitabweichungen
Fortsetzung des Artikels von Teil 1
Laufzeit als Funktion der Frequenz
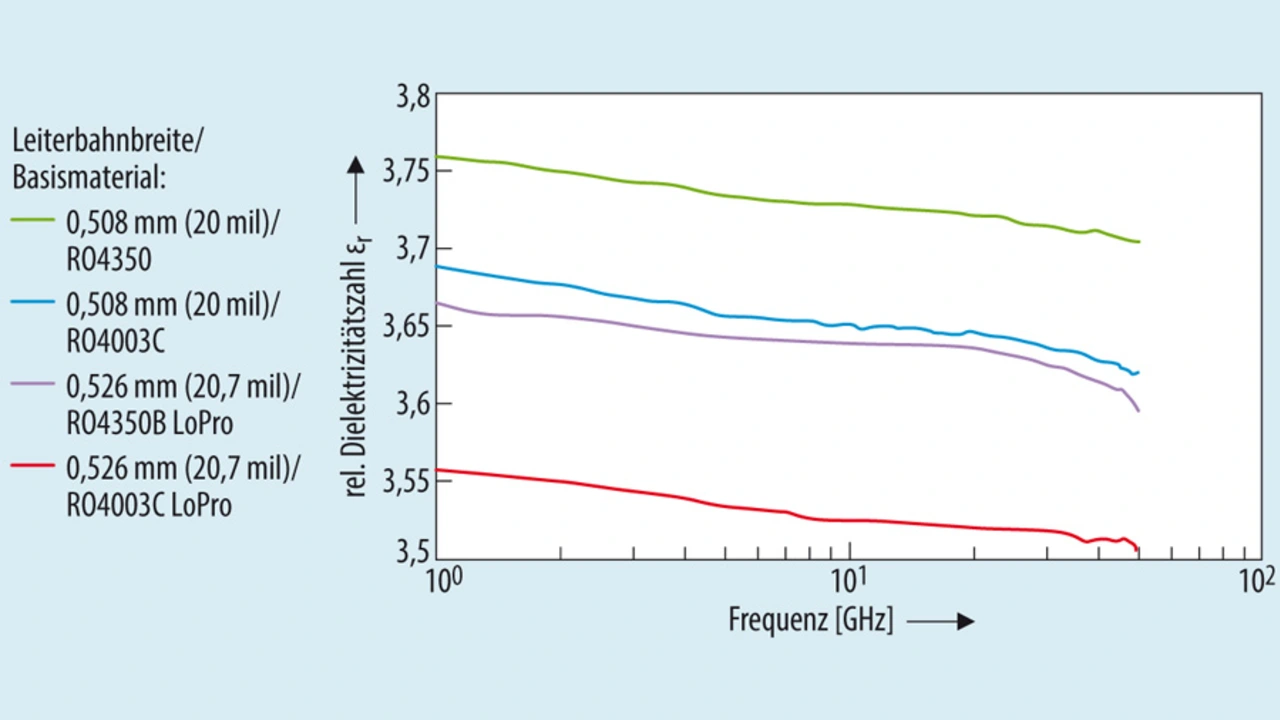
Die auf Pikosekunden genaue Anpassung der Laufzeiten von Signalen unterschiedlicher Frequenz gestaltet sich wegen der konträren Variablen recht anspruchsvoll. Aus Bild 1 ist zu entnehmen, dass die Dielektrizitätszahl in der Regel mit steigender Frequenz abnimmt. Gemäß den Gleichungen 1 und 2 ruft dieses Verhalten eine geringere Signallaufzeit (tS) hervor, wenn die Frequenz steigt. Auf der Basis von Gleichung 3 und dem Rogers-Basismaterial aus Bild 1 beträgt die Laufzeitdifferenz (ΔtS) zwischen zwei Sinuswellen mit Frequenzen von 1 GHz bzw. 20 GHz auf einer 10 cm langen Leiterbahn rund 4 ps [1].
Jobangebote+ passend zum Thema
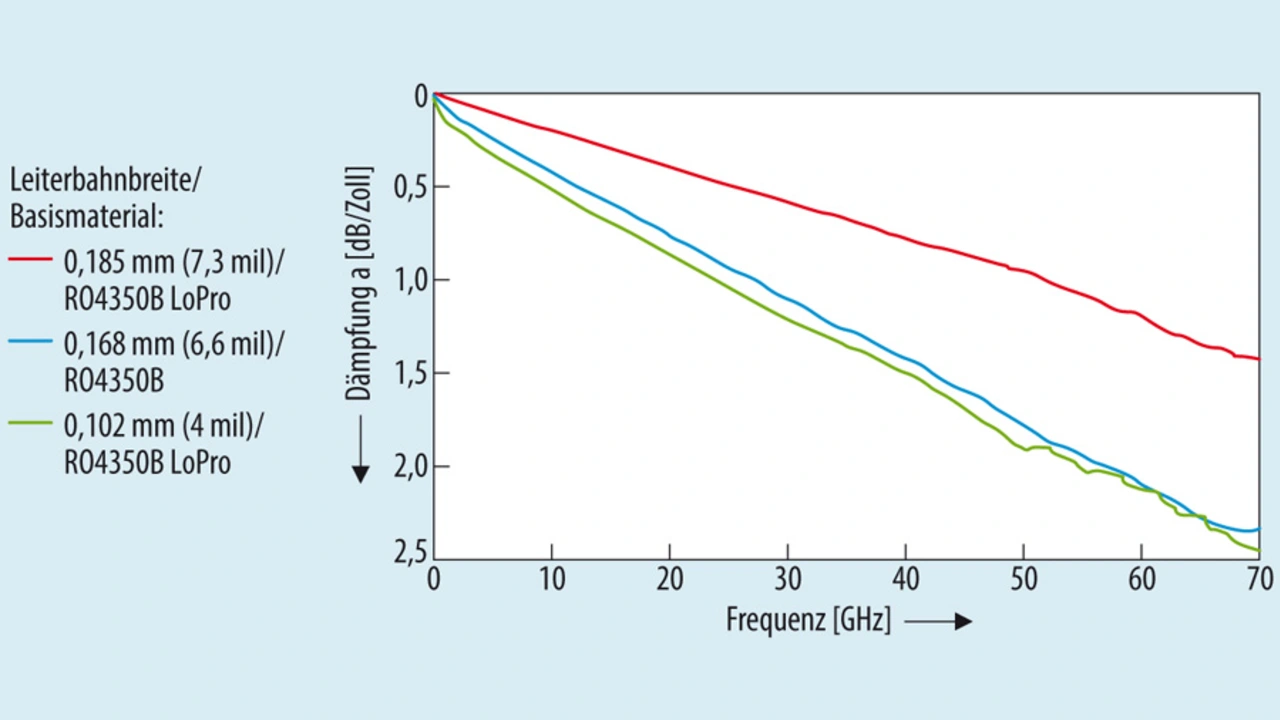
Aus Bild 2 ist ersichtlich, dass die Signalabschwächung mit steigender Frequenz zunimmt. Die in einer Rechteckwelle enthaltenen Oberschwingungen höherer Ordnung werden also stärker gedämpft als die Grundschwingung. Das Ausmaß, mit dem diese Filterwirkung erfolgt, sorgt für unterschiedliche Anstiegs- (tAn) und Abfallzeiten (tAb).
Eine Änderung von tAn oder tAb lässt die Welle am Takteingang des empfangenden Bausteins wie mit einer geänderten Gesamtlaufzeit erscheinen, die sich aus der Signallaufzeit (tS) der Leiterbahn und den tAn/2- oder tAb/2-Werten des Signals zusammensetzt.
Rechteckwellen unterschiedlicher Frequenz können überdies verschiedene Gruppenlaufzeiten aufweisen. Aus diesem Grund sind Rechteckwellen anspruchsvoller als Sinuswellen, wenn es um die Abschätzung der Laufzeitanpassung zwischen verschiedenen Frequenzen geht.
Zum besseren Verständnis der Dämpfung (a) als Funktion der Frequenz wird auf die Gleichungen 6 und 7 und die Literatur [2, 3, 4, 5] verwiesen, die in die Themen Verlustwinkel (δ) und den Skin-Effekt einführen. Ein entscheidender Aspekt aus dieser Literatur ist die Aussage, dass der Skin-Effekt die Fläche A in Gleichung 7 reduziert und damit den Leitungswiderstand R erhöht [3].
mit:
a = Dämpfung in db/Zoll,
f = Frequenz in GHz,
tan δ = Verlustfaktor des Materials,
εr eff = effektive relative Dielektrizitätszahl des Materials
mit:
ρ = spezifischer Widerstand
Um bei hohen Frequenzen eine übermäßige Abschwächung infolge des Skin-Effekts zu unterbinden, sollten keine nickelhaltigen Beschichtungen wie etwa Solder Mask Over Gold (SMOG) oder Electroless Nickel Immersion Gold (ENIG) verwendet werden [4, 5]. Ein Beispiel für eine ohne Nickel auskommende Beschichtung ist SMOBC (Solder Mask Over Bare Copper).
Zusammenfassend gilt also: Wählen Sie ein Basismaterial mit niedrigem εr und tan δ, verwenden Sie keine nickelhaltige Beschichtung und führen Sie für wichtige Leiterbahnen Simulationen der Signallaufzeit durch, um die Laufzeitanpassung für verschiedene Frequenzen zu verbessern.
Einfluss der Temperatur auf die Laufzeit
Die temperaturbedingten Schwankungen der Dielektrizitätszahl haben zur Folge, dass sich die Signallaufzeit der Leitung ändert. Gleichung 4 berechnet die Laufzeitdifferenz ΔtS bezogen auf die temperaturbedingten Änderungen der Dielektrizitätszahl.
Leiterplatten-Basismaterialien werden generell in Werkstoffe mit Glasgewebe und solche ohne Glasgewebe eingeteilt. HF-Basismaterialien mit Glasgewebe sind im Allgemeinen billiger und haben einen höheren εr -Wert, da Glas einen εr-Wert von 6 hat.
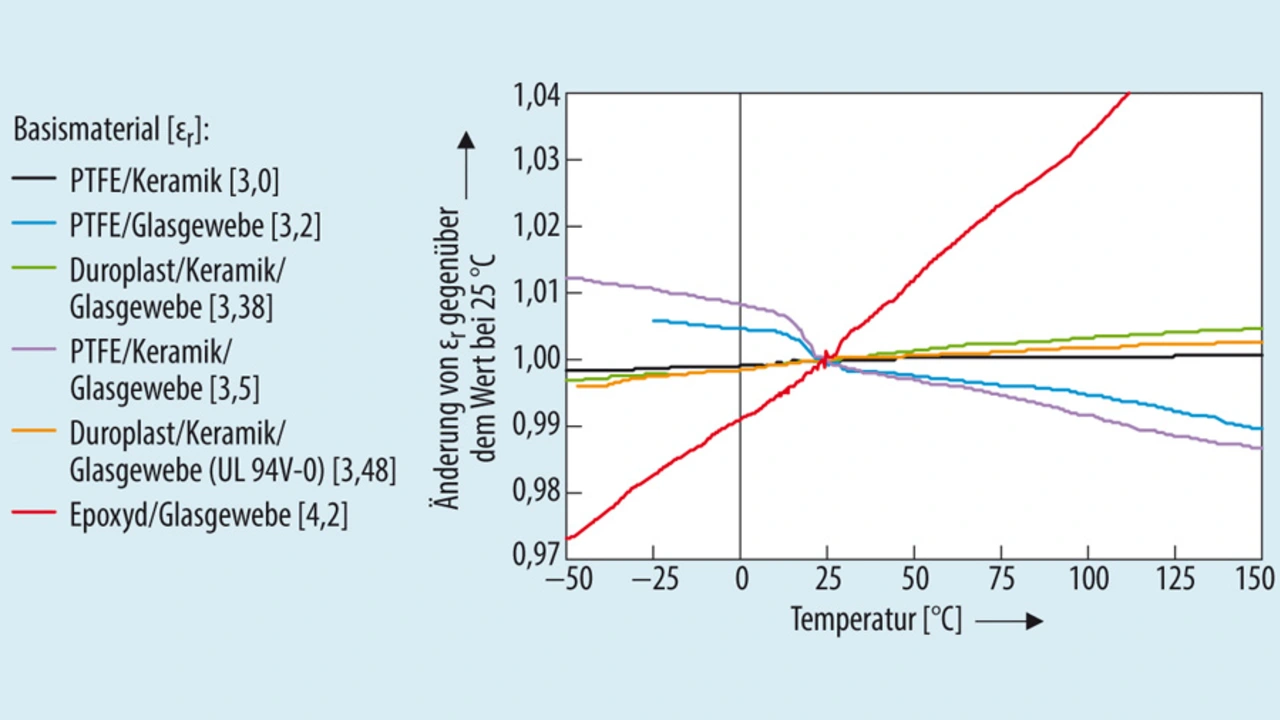
Bild 3 verdeutlicht die temperaturbedingten Änderungen von εr für verschiedene Werkstoffe. Es zeigt, dass einige auf PTFE und Glasgewebe basierende Materialien zwischen 10 °C und 25 °C eine steile Änderung des Temperaturkoeffizienten von εr aufweisen.
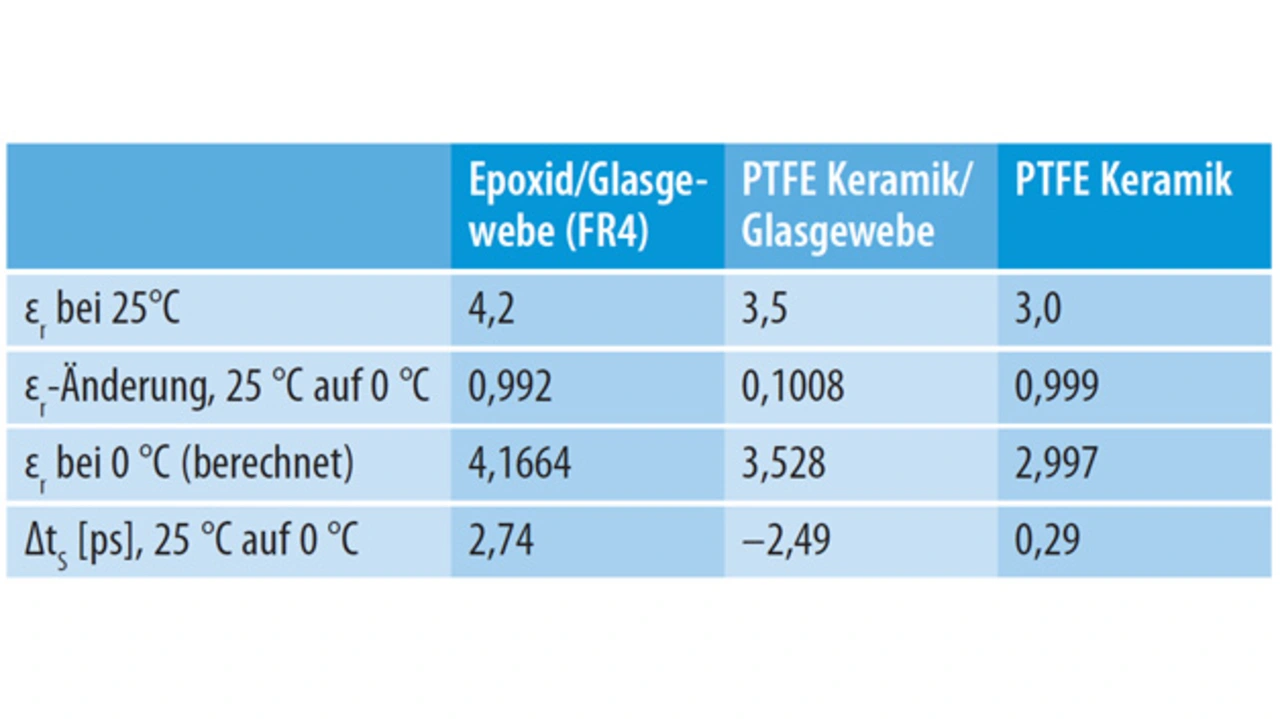
Auf der Basis der Gleichungen 3 und 4 wurde für eine 10 cm lange Streifenleitung auf unterschiedlichen Basismaterialien die Laufzeitdifferenz (ΔtS) für eine Temperaturänderung von 25 °C auf 0 °C berechnet (Tabelle 4).
In einem System, das eine Anpassung der Signallaufzeit für verschiedene Leiterbahnen bei unterschiedlichen Temperaturen erfordert, kann allein die Auswahl des Leiterplattenwerkstoffs zu Laufzeitabweichungen von einigen Pikosekunden zwischen 10 cm langen Leiterbahnen führen.
Ähnliche Aspekte zum TKε gelten für die Dielektrika von Koaxialkabeln. Da Koaxialkabel außerdem meist wesentlich länger sind als Leiterbahnen, ergibt sich ein deutlich höherer ΔtS-Wert über die Temperatur. Bei Verwendung zweier 1 m langer Kabel mit gleichen Eigenschaften (siehe Spalte 2 in Tabelle 4), können sich Laufzeitunterschiede von 25 ps einstellen, wenn sich die Temperatur von 25 °C auf 0 °C ändert.
Tabelle 4 geht von konstanten Temperaturen entlang der 10 cm langen Leiterbahn aus. In der Praxis muss die Temperatur jedoch über die gesamte Länge einer Leiterbahn oder eines Kabels keineswegs unbedingt gleich sein, so dass die Analyse komplexer ist als für das soeben umrissene Szenario.
- Neun Tipps zum Minimieren von Laufzeitabweichungen
- Laufzeit als Funktion der Frequenz
- Laufzeitangepasste Kabel
Lesen Sie mehr zum Thema
Das könnte Sie auch interessieren
Car-Camera-Bus-Technologie (C2B)
Fahrzeug-Kamera-Verbindung
Systemdesign / Safety&Security
Funktionale Sicherheit in der Datenerfassung
